An abelian category is a mathematical framework in which morphisms and objects behave similarly to abelian groups, allowing for kernels, cokernels, and exact sequences to be defined naturally. This structure provides a unifying setting for homological algebra and facilitates the study of complex algebraic phenomena across various fields. Explore the article to deepen your understanding of the properties and applications of abelian categories.
Table of Comparison
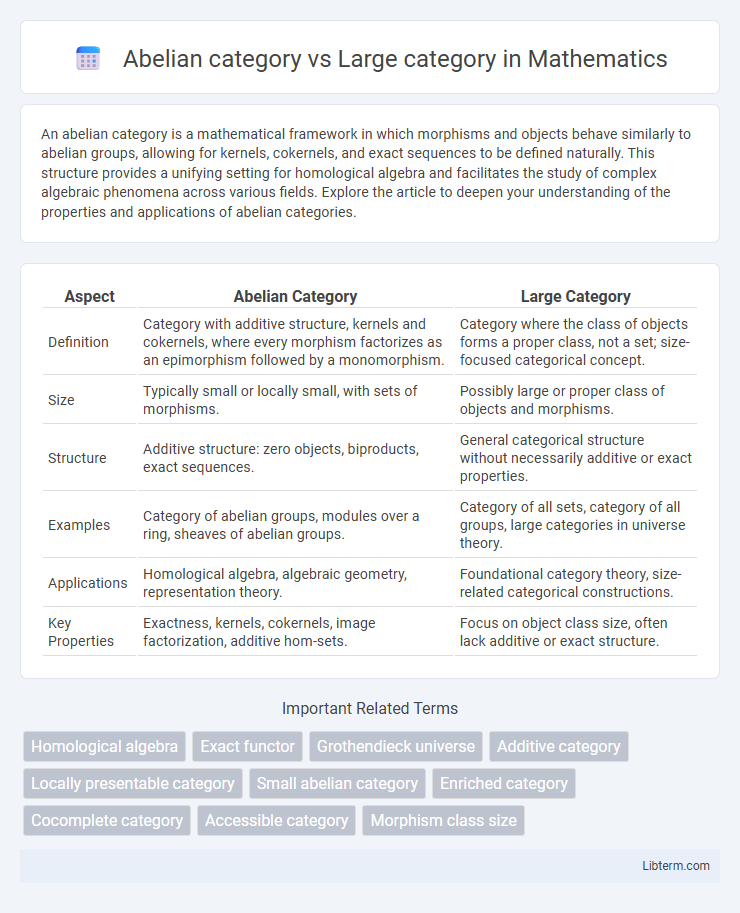
| Aspect | Abelian Category | Large Category |
|---|---|---|
| Definition | Category with additive structure, kernels and cokernels, where every morphism factorizes as an epimorphism followed by a monomorphism. | Category where the class of objects forms a proper class, not a set; size-focused categorical concept. |
| Size | Typically small or locally small, with sets of morphisms. | Possibly large or proper class of objects and morphisms. |
| Structure | Additive structure: zero objects, biproducts, exact sequences. | General categorical structure without necessarily additive or exact properties. |
| Examples | Category of abelian groups, modules over a ring, sheaves of abelian groups. | Category of all sets, category of all groups, large categories in universe theory. |
| Applications | Homological algebra, algebraic geometry, representation theory. | Foundational category theory, size-related categorical constructions. |
| Key Properties | Exactness, kernels, cokernels, image factorization, additive hom-sets. | Focus on object class size, often lack additive or exact structure. |
Overview of Abelian Categories
Abelian categories are foundational structures in homological algebra characterized by the presence of kernels, cokernels, and exact sequences, enabling a robust framework for dealing with modules and sheaves. Unlike large categories, which refer to categories of a size that may exceed set-theoretic limitations, Abelian categories are typically small or locally small, ensuring well-behaved morphisms and limits. The intrinsic exactness properties of Abelian categories facilitate the development of derived functors and cohomological theories essential in modern algebraic geometry and representation theory.
Defining Large Categories
Large categories are defined by having a proper class of objects rather than a set, distinguishing them from small and locally small categories where objects form sets. Abelian categories, fundamental in homological algebra, are often considered within small or locally small frameworks to ensure manageable structure and set-theoretic consistency. Understanding the foundational difference highlights how large categories generalize categorical concepts beyond set limitations, impacting constructions like limits, colimits, and exact sequences.
Key Differences Between Abelian and Large Categories
An Abelian category is a mathematically structured category where morphisms and objects behave similarly to abelian groups, ensuring kernels and cokernels exist and all monomorphisms and epimorphisms are normal. Large categories refer to categories whose collections of objects or morphisms form proper classes, not sets, making them broader in scale without intrinsic algebraic structure. The key differences lie in Abelian categories emphasizing exact sequences, additive structure, and homological algebra, whereas large categories are defined by size and set-theoretic considerations without guaranteed algebraic properties.
Structural Properties of Abelian Categories
Abelian categories exhibit rich structural properties, including the existence of kernels and cokernels for every morphism, which allow for well-defined notions of exact sequences and homological algebra. These categories are additive and have finite biproducts, ensuring that every morphism can be decomposed into an image and coimage, facilitating the study of module categories and derived functors. Large categories, on the other hand, may lack such strict additive and exactness properties, making Abelian categories fundamentally suitable for advanced algebraic structures and categorical homology theories.
Size Considerations in Large Categories
Large categories are characterized by having a proper class of objects rather than a set, which presents significant size considerations absent in Abelian categories typically defined as small or locally small. Abelian categories are structured with hom-sets that are sets, ensuring manageable cardinality for morphisms and objects, while large categories may encounter foundational issues related to class size and the necessity of universes or Grothendieck universes to avoid paradoxes. These size distinctions influence constructions like limits, colimits, and exact sequences, which are well-behaved in Abelian categories but require careful treatment in large categories due to their expansive object collections.
Examples of Abelian Categories
Abelian categories include crucial examples such as the category of abelian groups, the category of modules over a ring, and the category of coherent sheaves on a scheme, all of which provide a rich structure for homological algebra. In contrast, large categories often refer to categories with classes of objects too big to be sets, like the category of all sets or all groups, which may not have abelian properties. These examples highlight how abelian categories support kernels, cokernels, and exact sequences, unlike large categories that typically lack such well-behaved algebraic features.
Notable Instances of Large Categories
Notable instances of large categories include the category of all sets, the category of all groups, and the category of all topological spaces, each forming a foundational framework in mathematics but exceeding small category size constraints due to their proper class of objects. Abelian categories, such as the category of abelian groups or modules over a ring, are inherently small or locally small, equipped with exact sequences and additive structures that facilitate homological algebra. Large categories contrast with abelian categories by their vast object collections, posing unique challenges and requiring careful handling within category theory to avoid set-theoretic paradoxes.
Applications in Modern Mathematics
Abelian categories provide a foundational framework for homological algebra, facilitating the study of exact sequences and derived functors essential in algebraic geometry and representation theory. Large categories, often encompassing classes too extensive to be sets, enable the handling of vast mathematical structures, such as categories of all topological spaces or all groups, critical in higher category theory and topos theory. Both structures underpin modern advances in areas like sheaf theory, cohomology, and homotopy theory, where managing precise algebraic and categorical properties is crucial for deep theoretical insights.
Limitations and Challenges
Abelian categories, essential in homological algebra, are limited by their strict axioms requiring exact sequences and additive structure, which restricts their application to more general or large categories. Large categories, often not small or locally small, pose challenges in foundational set theory, complicating the formation of limits, colimits, and the development of a well-behaved homological framework. These limitations hinder the seamless extension of abelian category tools into large categories, necessitating alternative approaches or stronger set-theoretical assumptions for effective categorical analysis.
Choosing the Right Category for Mathematical Contexts
Abelian categories provide a well-structured framework with exact sequences and kernels, ideal for homological algebra and cohomology theories, ensuring additive and exactness properties that facilitate algebraic computations. Large categories, typically encompassing classes too big to be sets, are suited for contexts requiring expansive collections of objects, such as the category of all groups or all sets, but they lack the intrinsic algebraic structure found in Abelian categories. Selecting the right category depends on balancing the need for algebraic rigor with the scope of objects, where Abelian categories excel in linear and additive contexts, while large categories handle broad universes of mathematical structures.
Abelian category Infographic
 libterm.com
libterm.com