The tensor product combines two algebraic structures into a new one, preserving their properties and enabling complex operations in fields like linear algebra and quantum mechanics. This operation is fundamental for describing multi-dimensional spaces and transforming data across various mathematical frameworks. Explore the rest of the article to understand how the tensor product enhances your computational and theoretical toolkit.
Table of Comparison
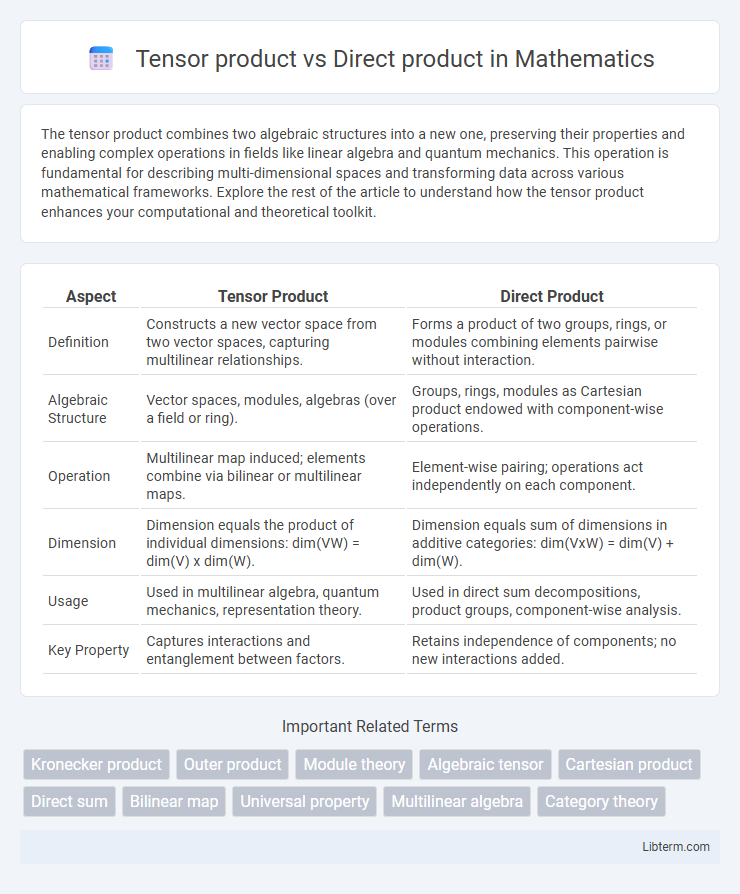
| Aspect | Tensor Product | Direct Product |
|---|---|---|
| Definition | Constructs a new vector space from two vector spaces, capturing multilinear relationships. | Forms a product of two groups, rings, or modules combining elements pairwise without interaction. |
| Algebraic Structure | Vector spaces, modules, algebras (over a field or ring). | Groups, rings, modules as Cartesian product endowed with component-wise operations. |
| Operation | Multilinear map induced; elements combine via bilinear or multilinear maps. | Element-wise pairing; operations act independently on each component. |
| Dimension | Dimension equals the product of individual dimensions: dim(VW) = dim(V) x dim(W). | Dimension equals sum of dimensions in additive categories: dim(VxW) = dim(V) + dim(W). |
| Usage | Used in multilinear algebra, quantum mechanics, representation theory. | Used in direct sum decompositions, product groups, component-wise analysis. |
| Key Property | Captures interactions and entanglement between factors. | Retains independence of components; no new interactions added. |
Introduction to Tensor Product and Direct Product
Tensor product constructs a new vector space from two vector spaces, enabling multilinear mappings and capturing intricate interactions between elements, essential in quantum mechanics and multilinear algebra. Direct product combines two algebraic structures, such as groups or vector spaces, into a product structure where each component operates independently, preserving the properties of the original structures. Tensor products emphasize bilinearity and complex combinations, while direct products focus on parallel composition without intertwining the individual elements.
Mathematical Foundations of Tensor and Direct Products
Tensor products derive from multilinear algebra, enabling the construction of new vector spaces from pairs of vector spaces by encoding bilinear maps through a universal property, essential in defining multilinear forms and modules over rings. Direct products form a product space by combining elements from each component space without intertwining their structures, primarily used to analyze product groups, modules, or vector spaces through coordinate-wise operations. These foundational differences influence their algebraic properties: tensor products capture interactions between spaces via bilinearity, whereas direct products preserve independent component operations.
Definitions: Tensor Product vs Direct Product
The tensor product of two vector spaces V and W over a field F is a new vector space V W that encodes bilinear maps from V x W into another vector space, constructed to satisfy a universal property ensuring multilinear compatibility. In contrast, the direct product (or direct sum in finite dimensions) of V and W, denoted V x W or V W, is the vector space consisting of ordered pairs (v, w) with componentwise addition and scalar multiplication, representing independent combinations of elements from each space. The tensor product emphasizes multilinear interaction and dimension multiplication (dim(V W) = dim(V) * dim(W)), while the direct product maintains separate structures with dimension addition (dim(V x W) = dim(V) + dim(W)).
Key Differences Between Tensor Product and Direct Product
The tensor product of two vector spaces produces a new vector space that encodes bilinear maps and allows for multilinear algebra operations, whereas the direct product forms a Cartesian product combining elements without introducing new algebraic structure beyond component-wise operations. Tensor products are utilized for constructing spaces where linear maps become compatible with the algebraic structure, often used in quantum mechanics and representation theory. In contrast, direct products preserve individual component identities and are applied in contexts emphasizing independent component behavior, such as product groups or module constructions.
Applications in Linear Algebra and Vector Spaces
The tensor product constructs a new vector space that encodes bilinear maps, essential in multilinear algebra for transforming and analyzing linear relations between vector spaces. The direct product forms a vector space by pairing elements from each space without mixing their structures, commonly used to handle systems composed of independent vector spaces. Tensor products facilitate applications in differential geometry and quantum computing by enabling complex interactions, while direct products simplify problems involving Cartesian products of vector spaces.
Role in Module and Group Theory
The tensor product in module theory constructs a new module that linearizes bilinear maps, enabling the combination of two modules over a ring into a single module capturing multilinear relationships, while the direct product creates a module consisting of ordered pairs from each module, preserving individual module structures independently. In group theory, the direct product forms a group whose elements are ordered pairs from two groups with component-wise operation, maintaining each group's structure, whereas the tensor product is less commonly defined but related to modules over group rings and used in homological algebra to study extensions and representations. The tensor product's role in connecting modules via multilinear maps contrasts with the direct product's role in combining group or module elements component-wise without interaction.
Examples Illustrating Tensor Product and Direct Product
The tensor product of vector spaces V and W, denoted V W, combines elements like (v, w) into formal sums capturing bilinearity, exemplified by R2 R3 yielding a 6-dimensional space where basis vectors e_i f_j represent all pairs. The direct product V x W constructs ordered pairs from elements of V and W, maintaining component-wise operations, such as R2 x R3 being a 5-dimensional space of pairs (v, w) without blending basis elements. Tensor products model multilinear mappings and quantum states, while direct products describe independent structures or combined systems retaining separate identities.
Notation and Formal Properties
The tensor product \( V \otimes W \) of vector spaces \( V \) and \( W \) is denoted by \( \otimes \) and is characterized by bilinearity, universal property, and construction of a new vector space capturing multilinear maps, whereas the direct product \( V \times W \) uses the symbol \( \times \) and represents ordered pairs with componentwise addition and scalar multiplication. Formally, the dimension of the tensor product satisfies \(\dim(V \otimes W) = \dim(V) \times \dim(W)\), while the direct product dimension is \(\dim(V \times W) = \dim(V) + \dim(W)\). The tensor product is associative and distributes over direct sums, important for module theory and multilinear algebra, contrasting the direct product's simpler but less algebraically rich structure.
Pros and Cons of Each Product
Tensor products enable the construction of new vector spaces by combining existing ones, preserving multilinear structures and allowing applications in quantum mechanics and representation theory, but they can be computationally intensive and may lead to complex, high-dimensional spaces. Direct products simplify combining groups, rings, or modules by forming coordinate-wise operations, facilitating easier analysis and decompositions, yet they often lack the richer interaction captured by tensor products and may not reflect entangled or intertwined structures. Choosing between tensor and direct products depends on whether the goal is to maintain linearity and capture interactions (favoring tensor products) or to create straightforward, separable composite structures (favoring direct products).
Summary and Practical Implications
The tensor product combines vector spaces or modules to create a new structure capturing bilinear interactions, widely used in quantum mechanics and multilinear algebra for encoding entangled states and multilinear maps. The direct product forms a Cartesian product of groups or spaces, preserving individual components' operations independently and facilitating parallel computations and decompositions in algebraic structures. Practical applications of tensor products include constructing complex quantum states and multilinear forms, whereas direct products enable modular system design and simplify group theory problems.
Tensor product Infographic
 libterm.com
libterm.com