Universal enveloping algebra provides a powerful framework that bridges Lie algebras with associative algebras, allowing the representation of Lie algebra elements as linear transformations. It plays a crucial role in studying the structure and representations of Lie algebras, facilitating applications in mathematical physics and differential equations. Explore the rest of the article to deepen your understanding of how universal enveloping algebras function and their significance in advanced algebra.
Table of Comparison
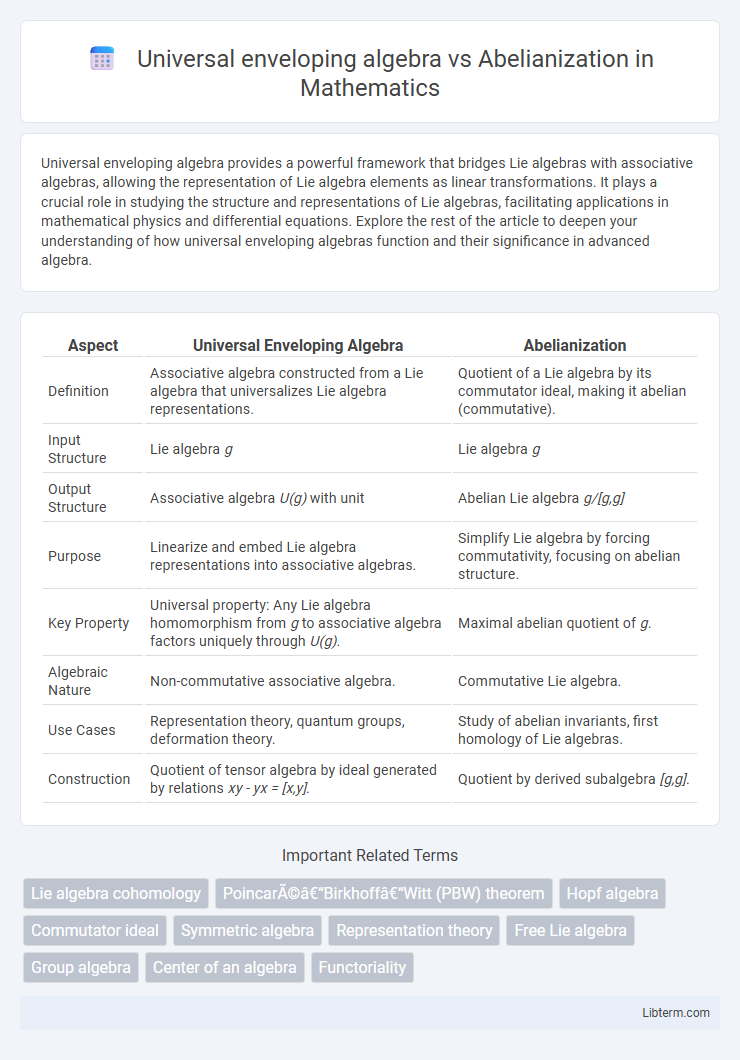
| Aspect | Universal Enveloping Algebra | Abelianization |
|---|---|---|
| Definition | Associative algebra constructed from a Lie algebra that universalizes Lie algebra representations. | Quotient of a Lie algebra by its commutator ideal, making it abelian (commutative). |
| Input Structure | Lie algebra g | Lie algebra g |
| Output Structure | Associative algebra U(g) with unit | Abelian Lie algebra g/[g,g] |
| Purpose | Linearize and embed Lie algebra representations into associative algebras. | Simplify Lie algebra by forcing commutativity, focusing on abelian structure. |
| Key Property | Universal property: Any Lie algebra homomorphism from g to associative algebra factors uniquely through U(g). | Maximal abelian quotient of g. |
| Algebraic Nature | Non-commutative associative algebra. | Commutative Lie algebra. |
| Use Cases | Representation theory, quantum groups, deformation theory. | Study of abelian invariants, first homology of Lie algebras. |
| Construction | Quotient of tensor algebra by ideal generated by relations xy - yx = [x,y]. | Quotient by derived subalgebra [g,g]. |
Introduction to Universal Enveloping Algebra
Universal enveloping algebra provides a powerful construction that associates a Lie algebra with an associative algebra, enabling the study of Lie algebra representations through module theory. It consists of an associative algebra containing the Lie algebra as a Lie subalgebra, preserving the Lie bracket via commutators while allowing the use of algebraic tools from ring theory. Abelianization, in contrast, simplifies structures by forcing commutativity, thus contrasting with the complexity captured in universal enveloping algebras which retain the non-commutative Lie bracket operations.
Defining Abelianization of Lie Algebras
Abelianization of Lie algebras is the process of forming the quotient of the Lie algebra by its derived subalgebra, effectively forcing the Lie bracket to become trivial and rendering the algebra Abelian. In contrast, the universal enveloping algebra is constructed as an associative algebra that contains the Lie algebra and encodes its Lie bracket via commutators. Abelianization simplifies the structure by collapsing all non-commuting elements, while the universal enveloping algebra preserves the full Lie structure within an associative framework.
Universal Enveloping Algebra: Key Properties
The Universal Enveloping Algebra (UEA) of a Lie algebra encapsulates its structure within an associative algebra, preserving the Lie bracket through commutators. Key properties include the Poincare-Birkhoff-Witt (PBW) theorem, which guarantees a basis of the UEA constructed from ordered monomials of Lie algebra elements. Unlike Abelianization, which simplifies a Lie algebra by forcing commutativity, the UEA retains intricate non-commutative relationships critical for representation theory and module construction.
Abelianization: Fundamental Concepts
Abelianization transforms a non-commutative algebraic structure into its largest commutative quotient by factoring out the commutator ideal, making it essential for simplifying Lie algebras. This process contrasts with the universal enveloping algebra, which embeds a Lie algebra into a non-commutative associative algebra retaining Lie bracket relations. Abelianization is crucial in representation theory and homological algebra, as it reveals the abelian invariants underlying complex algebraic systems.
Construction Methods Compared
The universal enveloping algebra of a Lie algebra is constructed via the tensor algebra of the vector space followed by quotienting by the ideal generated by relations encoding the Lie bracket, ensuring non-commutative multiplication reflecting the original Lie structure. Abelianization, in contrast, is formed by quotienting the Lie algebra by its commutator subalgebra, producing a commutative Lie algebra where all brackets vanish, thus simplifying its structure. The universal enveloping algebra preserves the non-abelian properties through a noncommutative associative algebra, whereas abelianization collapses those properties to yield a purely commutative object.
Algebraic Structures: Differences and Similarities
Universal enveloping algebra constructs a non-commutative algebra from a Lie algebra, preserving its Lie bracket structure through associative multiplication. Abelianization converts a Lie algebra or group into a commutative structure by factoring out the commutator subalgebra, effectively turning the bracket or group operation into an abelian operation. Both processes simplify algebraic structures but serve contrasting purposes: the universal enveloping algebra embeds non-commutative Lie algebra into associative algebra, while abelianization imposes commutativity by quotienting, highlighting fundamental differences in algebraic structure transformation.
Role in Representation Theory
The universal enveloping algebra of a Lie algebra encodes its representations by providing an associative algebra framework in which Lie algebra modules correspond to module structures over this algebra. Abelianization simplifies a Lie algebra to its maximal abelian quotient, often reducing representation complexity but losing non-commutative structure critical for capturing full representation behavior. In representation theory, the universal enveloping algebra enables detailed study of representations through its structure and ideals, while abelianization primarily aids in understanding characters and one-dimensional representations.
Applications in Mathematical Physics
Universal enveloping algebras play a crucial role in mathematical physics by providing a framework for representing Lie algebras, enabling the study of symmetry operations in quantum mechanics and quantum field theory. Abelianization simplifies non-commutative Lie algebras into commutative ones, facilitating the analysis of conserved quantities and integrable systems in statistical mechanics and gauge theories. These tools together allow for a deeper understanding of particle interactions, symmetry breaking, and the algebraic structures underlying physical laws.
Examples Illustrating Both Concepts
The universal enveloping algebra of a Lie algebra g, such as the Lie algebra sl(2, C), is a non-commutative associative algebra that encodes the Lie bracket relations and allows for representation theory analysis. Abelianization, exemplified by taking the Lie algebra of matrices and imposing commutativity relations, converts g into a commutative Lie algebra by factoring out the commutator ideal, yielding a simpler algebraic structure like a vector space with zero Lie bracket. For instance, the universal enveloping algebra U(sl(2, C)) captures all polynomial expressions in sl(2, C), while its abelianization reduces sl(2, C) to an abelian Lie algebra, losing the nontrivial bracket structure essential for representation.
Summary: Universal Enveloping Algebra vs. Abelianization
Universal enveloping algebra constructs a non-commutative algebra from a Lie algebra by embedding it into an associative algebra, preserving Lie brackets as commutators. Abelianization simplifies a Lie algebra by factoring out the commutator subalgebra, resulting in a commutative Lie algebra equivalent to its abelian quotient. The universal enveloping algebra encodes the entire Lie algebra's structure, while abelianization extracts its commutative essence.
Universal enveloping algebra Infographic
 libterm.com
libterm.com