Monomorphism in programming refers to functions or operations that operate on a single data type, ensuring predictable and efficient behavior. This concept enhances code clarity and type safety by limiting the scope of type variations. Explore the rest of the article to understand how monomorphism can improve your software development practices.
Table of Comparison
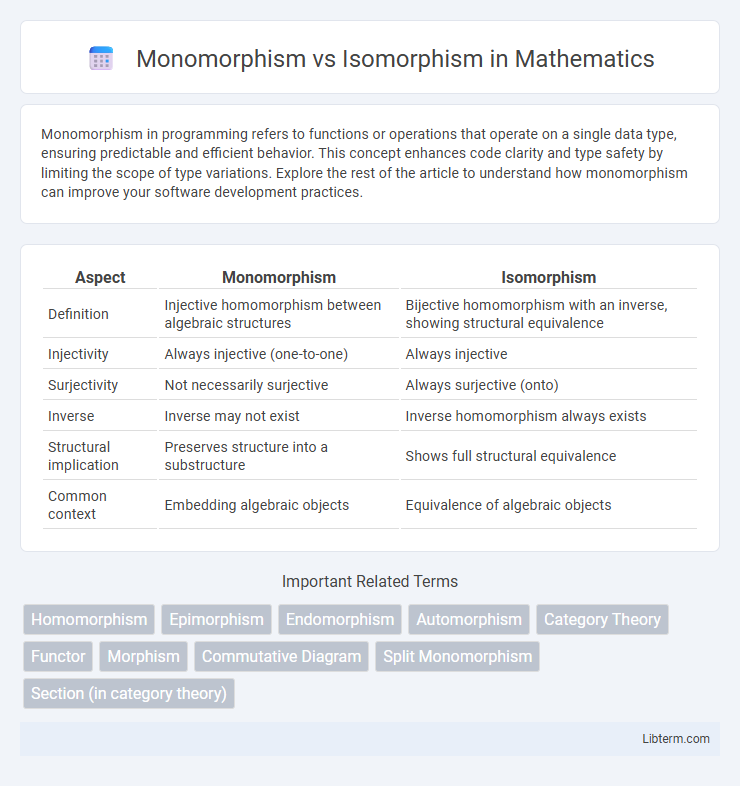
| Aspect | Monomorphism | Isomorphism |
|---|---|---|
| Definition | Injective homomorphism between algebraic structures | Bijective homomorphism with an inverse, showing structural equivalence |
| Injectivity | Always injective (one-to-one) | Always injective |
| Surjectivity | Not necessarily surjective | Always surjective (onto) |
| Inverse | Inverse may not exist | Inverse homomorphism always exists |
| Structural implication | Preserves structure into a substructure | Shows full structural equivalence |
| Common context | Embedding algebraic objects | Equivalence of algebraic objects |
Introduction to Monomorphism and Isomorphism
Monomorphism refers to a structure-preserving injective (one-to-one) mapping between algebraic structures, ensuring no two distinct elements in the domain map to the same element in the codomain. Isomorphism is a bijective (one-to-one and onto) homomorphism that establishes a one-to-one correspondence between two structures, indicating they are structurally identical. These concepts are fundamental in category theory and abstract algebra for analyzing object and morphism relationships.
Defining Monomorphism: Meaning and Examples
Monomorphism in category theory refers to a morphism that is injective or left-cancellable, meaning it preserves distinctness by mapping different elements to different elements. An example is the inclusion map from a subset to its superset, which is a monomorphism because it uniquely identifies elements without collapsing them. Monomorphisms are crucial for defining subobjects and understanding structural embeddings in various mathematical contexts.
Understanding Isomorphism: Definition and Illustration
Isomorphism in mathematics and computer science refers to a bijective mapping between two structures that preserves operations and relations, ensuring structural equivalence. For example, two graphs are isomorphic if there exists a one-to-one correspondence between their vertices and edges that maintains adjacency. Understanding isomorphism is crucial for identifying when two seemingly different structures are fundamentally the same in form and function.
Key Differences Between Monomorphism and Isomorphism
Monomorphism refers to an injective homomorphism where each element of the source structure maps to a unique element in the target, ensuring no two distinct elements share the same image. Isomorphism is a bijective homomorphism that establishes a perfect one-to-one correspondence between two structures, preserving operations and allowing reversible mapping. The key difference lies in monomorphisms being injective only, while isomorphisms require both injectivity and surjectivity, establishing structural equivalence.
Types of Monomorphisms in Mathematics
Monomorphisms in mathematics, particularly in category theory and algebra, refer to injective structure-preserving maps that embed one object into another without collapsing distinct elements. Types of monomorphisms include regular monomorphisms, which are equalizers of some pair of morphisms; split monomorphisms, which have a left inverse ensuring retraction; and extremal monomorphisms, defined by the property that any factorization through an epimorphism must be an isomorphism. Understanding these distinctions is crucial for analyzing object embeddings and morphism factorization in various mathematical structures.
Types of Isomorphisms Across Mathematical Structures
Isomorphisms in mathematics manifest in various types such as group isomorphisms, ring isomorphisms, and vector space isomorphisms, each preserving specific algebraic structures and operations. Group isomorphisms maintain group operations and identity elements, while ring isomorphisms preserve both addition and multiplication structures, ensuring an equivalence of rings. Vector space isomorphisms conserve vector addition and scalar multiplication, establishing a structural equivalence that indicates two vector spaces have the same dimension and linear properties.
Applications of Monomorphism in Algebra and Topology
Monomorphisms serve as injective homomorphisms crucial for embedding algebraic structures such as groups, rings, and modules into larger contexts, preserving the structure without loss of information. In topology, monomorphisms often appear as embeddings that maintain topological properties and facilitate the study of subspaces through continuous injective maps. These applications enable rigorous analysis of subobjects and contribute to the construction of categorical diagrams and exact sequences that are foundational in homological algebra and algebraic topology.
Practical Uses of Isomorphism in Real-World Problems
Isomorphism enables efficient solutions in graph theory by identifying structural equivalences between networks, facilitating data integration, and pattern recognition. In chemistry, it helps compare molecular structures, ensuring accurate predictions of chemical reactions and properties. Software engineering leverages isomorphic structures to optimize code reuse and simplify complex system modeling by preserving functional equivalence.
Comparing Monomorphism and Isomorphism: A Summary Table
Monomorphism is a morphism that is injective, preserving distinctness between elements, while isomorphism is a bijective morphism that establishes a structural equivalence between objects. Monomorphisms ensure one-to-one mappings without reverse guarantees, whereas isomorphisms provide both injective and surjective mappings with invertibility. The comparison summary highlights that every isomorphism is a monomorphism, but not all monomorphisms are isomorphisms, emphasizing their distinct roles in category theory and algebraic structures.
Conclusion: Choosing Between Monomorphism and Isomorphism
Choosing between monomorphism and isomorphism depends on the desired level of structural preservation and invertibility in mathematical mappings. Monomorphisms ensure injective structure-preserving mappings without requiring invertibility, making them suitable for embedding substructures. Isomorphisms require bijective, invertible mappings that preserve structure entirely, ideal for demonstrating equivalence between algebraic or topological objects.
Monomorphism Infographic
 libterm.com
libterm.com