An essential singularity is a point at which a complex function exhibits extremely wild behavior, where the function fails to have a Taylor or Laurent series that terminates with a finite number of principal part terms. Near this point, the function takes on every possible complex value, with at most one exception, infinitely often, a property described by the Casorati-Weierstrass theorem. Explore the rest of the article to understand how essential singularities influence function behavior and their applications in complex analysis.
Table of Comparison
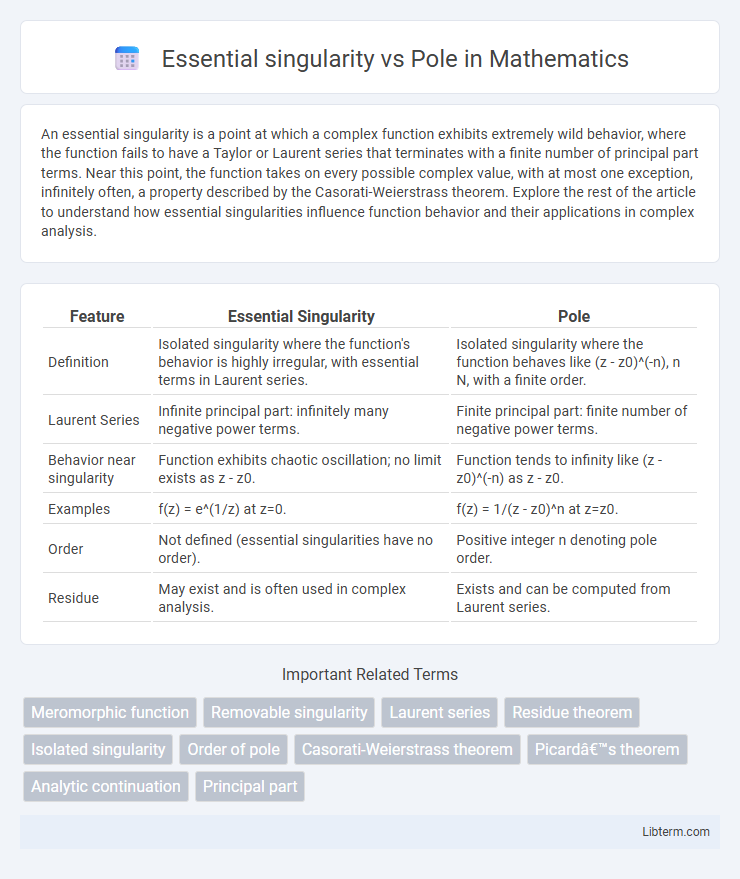
| Feature | Essential Singularity | Pole |
|---|---|---|
| Definition | Isolated singularity where the function's behavior is highly irregular, with essential terms in Laurent series. | Isolated singularity where the function behaves like (z - z0)^(-n), n N, with a finite order. |
| Laurent Series | Infinite principal part: infinitely many negative power terms. | Finite principal part: finite number of negative power terms. |
| Behavior near singularity | Function exhibits chaotic oscillation; no limit exists as z - z0. | Function tends to infinity like (z - z0)^(-n) as z - z0. |
| Examples | f(z) = e^(1/z) at z=0. | f(z) = 1/(z - z0)^n at z=z0. |
| Order | Not defined (essential singularities have no order). | Positive integer n denoting pole order. |
| Residue | May exist and is often used in complex analysis. | Exists and can be computed from Laurent series. |
Introduction to Essential Singularity and Pole
An essential singularity is a point where a complex function exhibits highly irregular behavior, causing its Laurent series to have infinitely many negative power terms, unlike a pole that has a finite order with a limited number of negative powers. Near an essential singularity, the function's values can oscillate wildly and do not approach any limit, whereas near a pole, the function tends to infinity in a specific manner characterized by the pole's order. Understanding the distinction between essential singularities and poles is crucial in complex analysis for classifying singular points and predicting function behavior around these points.
Defining Essential Singularity
An essential singularity is a point at which a complex function exhibits highly irregular behavior, characterized by the function's values not approaching any specific limit, unlike poles where the function tends to infinity in a predictable manner. According to the Casorati-Weierstrass theorem, near an essential singularity, the function's values come arbitrarily close to every complex number, showing a dense range. This contrasts sharply with a pole, which is a type of isolated singularity where the function's magnitude grows without bound as it approaches the point.
What is a Pole in Complex Analysis?
A pole in complex analysis is a type of isolated singularity where a complex function approaches infinity as the variable nears the singular point. It is characterized by the function behaving like \( \frac{1}{(z - z_0)^n} \) near the pole \( z_0 \), with \( n \) being a positive integer called the order of the pole. Unlike essential singularities, poles have well-defined behavior and can be classified by their order, making them isolated points where the function's magnitude diverges in a predictable algebraic manner.
Key Differences Between Essential Singularity and Pole
Essential singularities exhibit unpredictable behavior where the function's values near the point can oscillate wildly and take on almost any complex number, as characterized by the Casorati-Weierstrass theorem. In contrast, a pole is a type of singularity where the function tends to infinity in a controlled manner, often expressed as a finite principal part in the Laurent series expansion. Key differences include the nature of the singularity's approach--essential singularities lack a finite order and can cause dense value distributions near the point, while poles have finite order and involve limits diverging to infinity.
Mathematical Characterization of Essential Singularities
An essential singularity is characterized by the failure of a function to have a Laurent series with a finite principal part, exhibiting infinitely many negative powers and erratic behavior near the singularity. Unlike a pole, where the function's Laurent series contains finitely many negative powers and tends to infinity at the singularity, an essential singularity causes the function to attain every complex value, with possibly one exception, infinitely often in any neighborhood of the point, as described by the Casorati-Weierstrass theorem. Mathematically, this distinction is evident because an essential singularity corresponds to an infinite order of pole-like terms, making the singularity non-removable and fundamentally different in the complex function's local behavior.
Order and Classification of Poles
An essential singularity is characterized by the fact that it is neither a pole nor a removable singularity, exhibiting highly oscillatory behavior near the singular point, while a pole is classified by its order, which is the smallest positive integer \(n\) such that \((z - z_0)^n f(z)\) is analytic and nonzero at \(z_0\). The order of a pole directly determines the nature of the Laurent series expansion, as the principal part contains a finite number of negative power terms corresponding to the pole's order. Classification of poles involves identifying these finite negative powers, distinguishing poles of order \(n\) from essential singularities where infinitely many negative powers exist in the Laurent series.
Examples of Essential Singularities
An essential singularity is characterized by a point where a complex function exhibits highly irregular behavior, such as the function \( e^{1/z} \) at \( z=0 \), infinitely oscillating and not reducible to a pole or removable singularity. In contrast, poles represent points where a function like \( \frac{1}{(z-a)^n} \) (for some positive integer \( n \)) diverges to infinity with a predictable Laurent series containing finitely many negative powers. Classic examples of essential singularities include \( e^{1/z} \) and \( \sin{\frac{1}{z}} \), both demonstrating the Picard theorem behavior by taking on nearly all complex values infinitely often near the singularity.
Examples of Poles in Complex Functions
Poles in complex functions represent isolated singularities where the function approaches infinity at a specific point, such as the function f(z) = 1/(z - a)^n, which has a pole of order n at z = a. A classic example is f(z) = 1/z, exhibiting a simple pole at z = 0, while functions like f(z) = 1/(z - 1)^2 demonstrate a pole of order two at z = 1. Unlike essential singularities, poles have a well-defined Laurent series with a finite number of negative power terms, making their behavior near the singularity more predictable.
Impact on Function Behavior: Essential Singularity vs Pole
Essential singularities cause functions to exhibit highly unpredictable and oscillatory behavior near the singularity, with the Laurent series having infinitely many negative-power terms. Poles result in more regular, predictable behavior with finite-order divergence, characterized by a finite number of negative-power terms in the Laurent series. The presence of an essential singularity can lead to dense values of the function in any neighborhood, while poles correspond to isolated infinities affecting growth rates in a controlled manner.
Applications and Significance in Mathematics
Essential singularities and poles play critical roles in complex analysis, with poles representing points where functions exhibit predictable, algebraic-type singular behavior, useful in residue calculus for evaluating complex integrals in physics and engineering. Essential singularities, characterized by drastically unpredictable behavior described by the Casorati-Weierstrass theorem, find applications in chaos theory and dynamical systems, highlighting function behavior near critical points. Their contrasting properties underpin fundamental tools in analytic continuation, contour integration, and the study of special functions in mathematical physics.
Essential singularity Infographic
 libterm.com
libterm.com