Semisimple structures play a crucial role in algebra, particularly in the study of modules and rings where they simplify complex decompositions into direct sums of simple components. These concepts are fundamental for understanding the behavior of linear transformations and representation theory. Explore the rest of the article to see how semisimple theory can enhance your grasp of advanced algebraic systems.
Table of Comparison
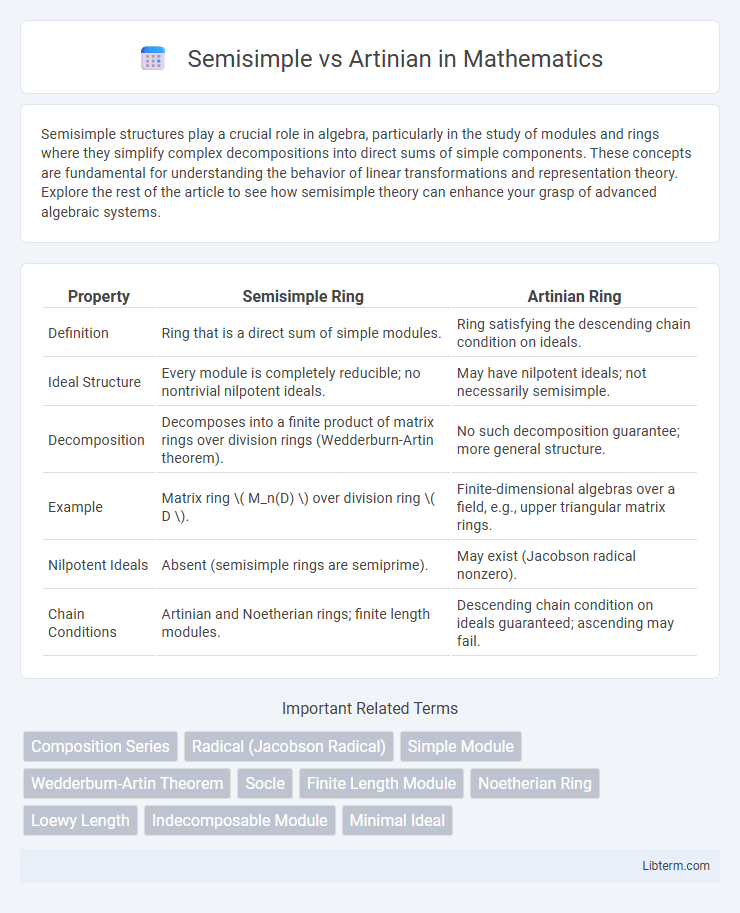
| Property | Semisimple Ring | Artinian Ring |
|---|---|---|
| Definition | Ring that is a direct sum of simple modules. | Ring satisfying the descending chain condition on ideals. |
| Ideal Structure | Every module is completely reducible; no nontrivial nilpotent ideals. | May have nilpotent ideals; not necessarily semisimple. |
| Decomposition | Decomposes into a finite product of matrix rings over division rings (Wedderburn-Artin theorem). | No such decomposition guarantee; more general structure. |
| Example | Matrix ring \( M_n(D) \) over division ring \( D \). | Finite-dimensional algebras over a field, e.g., upper triangular matrix rings. |
| Nilpotent Ideals | Absent (semisimple rings are semiprime). | May exist (Jacobson radical nonzero). |
| Chain Conditions | Artinian and Noetherian rings; finite length modules. | Descending chain condition on ideals guaranteed; ascending may fail. |
Introduction to Semisimple and Artinian Rings
Semisimple rings are characterized by their decomposition into a direct sum of simple modules, ensuring that every module is completely reducible. Artinian rings satisfy the descending chain condition on ideals, implying they have a well-structured and finite composition series. Understanding the distinction between semisimple and Artinian rings is fundamental in algebra, as semisimplicity concerns module decomposition while Artinian conditions govern ideal behavior and ring finiteness properties.
Historical Background and Motivation
Semisimple rings emerged from the work of Joseph Wedderburn in the early 20th century, classifying algebras decomposable into simple components, while Artinian rings were introduced to understand rings satisfying the descending chain condition on ideals, named after Emil Artin. The motivation behind studying semisimple rings centered on their structural clarity and direct sum decompositions, facilitating classification problems in algebra. Artinian rings broadened these insights by imposing finiteness conditions that ensured well-behaved module categories, linking ring theory to homological dimensions and representation theory.
Definitions: Semisimple Rings
Semisimple rings are algebraic structures in which every module is a direct sum of simple modules, ensuring complete reducibility. These rings are characterized by a zero Jacobson radical, indicating no nontrivial nilpotent ideals. In contrast to Artinian rings that satisfy descending chain conditions, semisimple rings focus on module decomposition into simple components.
Definitions: Artinian Rings
Artinian rings are algebraic structures characterized by the descending chain condition on ideals, meaning every descending sequence of ideals stabilizes after finitely many steps. These rings generalize finite-dimensional algebras and play a crucial role in ring theory due to their well-behaved module categories. In contrast to semisimple rings, Artinian rings may contain nilpotent elements but still ensure a controlled ideal structure critical for understanding ring decomposition.
Structural Differences Between Semisimple and Artinian
Semisimple rings decompose into a direct sum of simple modules, reflecting a completely reducible module structure characterized by zero Jacobson radical. Artinian rings satisfy the descending chain condition on ideals, ensuring finiteness properties but allowing nontrivial radicals and more complex module compositions. The key structural difference lies in semisimple rings being both Artinian and having no radical, while general Artinian rings may have nonzero Jacobson radicals, leading to a layered, non-semisimple module hierarchy.
Key Theorems and Characterizations
Semisimple rings are characterized by the Artin-Wedderburn theorem, which states they decompose into a finite direct product of matrix rings over division rings, highlighting their complete reducibility property. Artinian rings satisfy the descending chain condition on ideals, and a key characterization is that a semisimple ring is Artinian and has zero Jacobson radical. The Hopkins-Levitzki theorem further connects these concepts by proving that every Artinian ring is also Noetherian, reinforcing the structure theory of semisimple Artinian rings.
Examples: Semisimple Rings in Practice
Semisimple rings appear prominently as matrix rings over division rings, such as \( M_n(D) \) where \( D \) is a division ring, exemplifying classic semisimple structure. Group algebras over a field of characteristic zero, like \( \mathbb{C}[G] \) for a finite group \( G \), also provide practical instances of semisimple rings due to Maschke's theorem. In contrast, Artinian rings encompass semisimple rings but also include non-semisimple examples like local Artinian rings, which have nilpotent elements and are not direct sums of simple modules.
Examples: Artinian Rings in Practice
Artinian rings appear prominently in algebraic geometry and representation theory, with finite-dimensional algebras over fields serving as prime examples of semisimple Artinian rings. The ring of \( n \times n \) matrices over a field \( k \), \( M_n(k) \), exemplifies a simple Artinian ring, showcasing how semisimplicity corresponds to the absence of nontrivial two-sided ideals. Commutative Artinian rings, such as finite product rings like \( k[x]/(x^n) \), highlight the decomposition into a finite direct product of local Artinian rings, illustrating the interaction between Artinian conditions and ring structure.
Connections and Overlaps: When Semisimple Implies Artinian
Semisimple rings are always Artinian because their decomposition into simple modules ensures the descending chain condition on ideals. This overlap occurs since semisimple modules, being direct sums of simple modules, inherently satisfy the Artinian property. The structure theorem for semisimple rings guarantees finite length, making every semisimple ring both left and right Artinian.
Applications and Further Implications
Semisimple rings and Artinian rings play crucial roles in algebraic structures and representation theory due to their decomposition properties and finite-dimensional characteristics. Semisimple rings, characterized by their direct sum of simple modules, are essential in classifying modules and simplifying complex algebraic problems, while Artinian rings provide vital tools in dimension theory and ideal structure through their descending chain condition. The interplay between semisimplicity and Artinian conditions facilitates advancements in module theory, algebraic geometry, and homological algebra, impacting areas like coding theory, cryptography, and theoretical physics.
Semisimple Infographic
 libterm.com
libterm.com