The Dedekind eta function is a fundamental object in complex analysis and number theory, defined as an infinite product with deep connections to modular forms and partition theory. Its transformation properties under the modular group reveal significant insights into the symmetries of elliptic curves and modular surfaces. Explore the rest of this article to uncover how the Dedekind eta function plays a crucial role in modern mathematics.
Table of Comparison
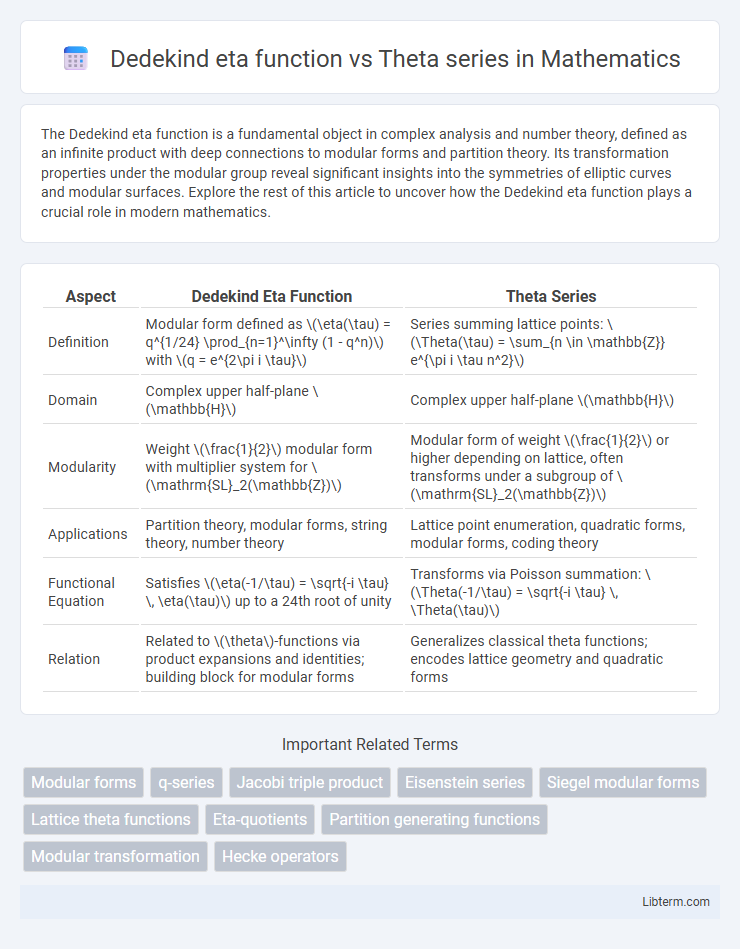
| Aspect | Dedekind Eta Function | Theta Series |
|---|---|---|
| Definition | Modular form defined as \(\eta(\tau) = q^{1/24} \prod_{n=1}^\infty (1 - q^n)\) with \(q = e^{2\pi i \tau}\) | Series summing lattice points: \(\Theta(\tau) = \sum_{n \in \mathbb{Z}} e^{\pi i \tau n^2}\) |
| Domain | Complex upper half-plane \(\mathbb{H}\) | Complex upper half-plane \(\mathbb{H}\) |
| Modularity | Weight \(\frac{1}{2}\) modular form with multiplier system for \(\mathrm{SL}_2(\mathbb{Z})\) | Modular form of weight \(\frac{1}{2}\) or higher depending on lattice, often transforms under a subgroup of \(\mathrm{SL}_2(\mathbb{Z})\) |
| Applications | Partition theory, modular forms, string theory, number theory | Lattice point enumeration, quadratic forms, modular forms, coding theory |
| Functional Equation | Satisfies \(\eta(-1/\tau) = \sqrt{-i \tau} \, \eta(\tau)\) up to a 24th root of unity | Transforms via Poisson summation: \(\Theta(-1/\tau) = \sqrt{-i \tau} \, \Theta(\tau)\) |
| Relation | Related to \(\theta\)-functions via product expansions and identities; building block for modular forms | Generalizes classical theta functions; encodes lattice geometry and quadratic forms |
Introduction to Dedekind Eta Function and Theta Series
The Dedekind eta function, defined as \( \eta(\tau) = e^{\pi i \tau / 12} \prod_{n=1}^\infty (1 - e^{2 \pi i n \tau}) \), is a modular form with significant applications in number theory and conformal field theory. Theta series are generating functions encoding the representation numbers of quadratic forms and are expressed as sums over lattice points with Gaussian weights, often taking the form \( \theta(\tau) = \sum_{n \in \mathbb{Z}} e^{\pi i n^2 \tau} \). Both functions exhibit modular transformation properties, connecting complex analysis, algebraic geometry, and arithmetic geometry through their role in the theory of modular forms and automorphic functions.
Historical Background and Mathematical Context
The Dedekind eta function, introduced by Richard Dedekind in the 19th century, is a modular form deeply connected to number theory and complex analysis through its product formula and transformation properties under the modular group. Theta series, originating from the work of Carl Gustav Jacobi, represent infinite series associated with quadratic forms and lattices, playing a crucial role in the theory of modular forms and automorphic functions. Both functions have foundational significance in understanding modular invariance, lattice point enumeration, and the arithmetic of elliptic curves.
Formal Definitions: Eta Function vs. Theta Series
The Dedekind eta function is formally defined as \(\eta(\tau) = e^{\pi i \tau/12} \prod_{n=1}^\infty (1 - e^{2\pi i n \tau})\), where \(\tau\) lies in the upper half-plane and encodes modular form properties. In contrast, a Theta series is typically expressed as \(\Theta(\tau) = \sum_{n \in \mathbb{Z}^d} e^{\pi i \tau Q(n)}\), involving a positive definite quadratic form \(Q\) over integer lattice points, serving as a generating function for lattice point counts. Both functions play a crucial role in number theory and modular forms but differ fundamentally in construction: the eta function is an infinite product reflecting partition-like behavior, whereas Theta series are infinite sums encoding geometric and arithmetic information of lattices.
Analytic Properties and Transformations
The Dedekind eta function, defined as e(t) = e^(pit/12) _{n=1}^ (1 - e^{2pint}), is a modular form of weight 1/2 with a well-known transformation behavior under SL(2,Z), exhibiting a precise multiplier system and functional equation. Theta series, constructed from quadratic forms, are typically modular forms or modular functions whose analytic properties include holomorphy and modular transformations characterized by weight, level, and character depending on the lattice involved. Both functions exhibit modular invariance but differ in their transformation formulas: e(t) transforms via a non-trivial multiplier system of order 24, whereas theta series transform with factors determined by their associated quadratic forms and Weil representation, crucial for studying automorphic forms and number theory.
Modular Forms: Role of Eta Function and Theta Series
The Dedekind eta function, defined as \(\eta(\tau) = e^{\pi i \tau/12} \prod_{n=1}^\infty (1 - e^{2\pi i n \tau})\), is a key modular form of weight 1/2 with a multiplier system, playing a crucial role in the construction of modular forms and their transformation properties under the modular group. Theta series, arising from quadratic forms and lattice sums, are modular forms or modular forms of half-integral weight, encoding arithmetic information such as representation numbers and exhibiting transformation behavior linked to the Weil representation. Both eta functions and theta series serve as fundamental building blocks in the theory of modular forms, with the eta function often used to generate cusp forms and the theta series employed to establish connections between modular forms and number theory.
Series Representations and Fourier Expansions
The Dedekind eta function is expressed as an infinite product \(\eta(\tau) = q^{1/24} \prod_{n=1}^\infty (1 - q^n)\), where \(q = e^{2\pi i \tau}\), providing a modular form with deep connections to partition theory. Theta series arise from quadratic forms and are represented as sums \(\theta(\tau) = \sum_{n \in \mathbb{Z}^m} e^{\pi i \tau Q(n)}\), yielding Fourier expansions encoding lattice point counts. Both functions' Fourier expansions reveal automorphic properties, with the eta function's coefficients linked to partition functions and the theta series coefficients enumerating representations by quadratic forms.
Connection to Partition Theory and Number Theory
The Dedekind eta function encodes partition numbers through its q-series expansion, linking modular forms to partition theory by generating integer partitions via its infinite product formula. Theta series represent quadratic forms and count lattice points, providing insight into number theory by connecting sums of squares to modular forms. Both functions serve as generating functions in number theory, revealing deep arithmetic properties and enabling the study of partition congruences and representation of integers.
Applications in Physics and Cryptography
The Dedekind eta function plays a crucial role in string theory and conformal field theory by encoding modular invariance and quantum partition functions, while theta series are fundamental in expressing lattice sums and characterizing solutions in solid-state physics and elliptic curve cryptography. Theta series facilitate efficient error correction and encryption algorithms through their connection to lattice-based cryptosystems, whereas the Dedekind eta function contributes to the formulation of partition functions and black hole entropy calculations. Both functions enable advanced cryptographic constructions and quantum computations by leveraging their deep modular transformation properties and number-theoretic foundations.
Comparative Analysis: Similarities and Differences
The Dedekind eta function and theta series both arise in the study of modular forms and exhibit transformation properties under the modular group, yet the eta function is a modular form of weight 1/2 with a product formula, while theta series typically represent sums over lattice points and can have various weights depending on the lattice dimension. The eta function encodes arithmetic information through its q-expansion and plays a crucial role in partition theory, whereas theta series encapsulate quadratic form data and serve as generating functions for lattice point counts. Their distinct constructions reflect different aspects of number theory and representation theory, with the eta function emphasizing multiplicative structures and theta series highlighting additive lattice symmetries.
Open Problems and Further Research Directions
The Dedekind eta function and Theta series both play pivotal roles in number theory and modular forms, yet several open problems remain, including the deeper characterization of their transformation properties under various modular groups. Research directions focus on exploring generalizations of the eta function in higher dimensions and uncovering novel connections between Theta series and automorphic representations. Investigating the relationships between these functions could lead to breakthroughs in understanding moonshine phenomena and explicating arithmetic properties of modular forms.
Dedekind eta function Infographic
 libterm.com
libterm.com