Choosing the right filter enhances air quality by removing pollutants, allergens, and dust particles effectively. High-efficiency filters capture microscopic contaminants, ensuring cleaner and healthier indoor environments. Explore the article to discover how selecting the perfect filter can improve Your air quality and well-being.
Table of Comparison
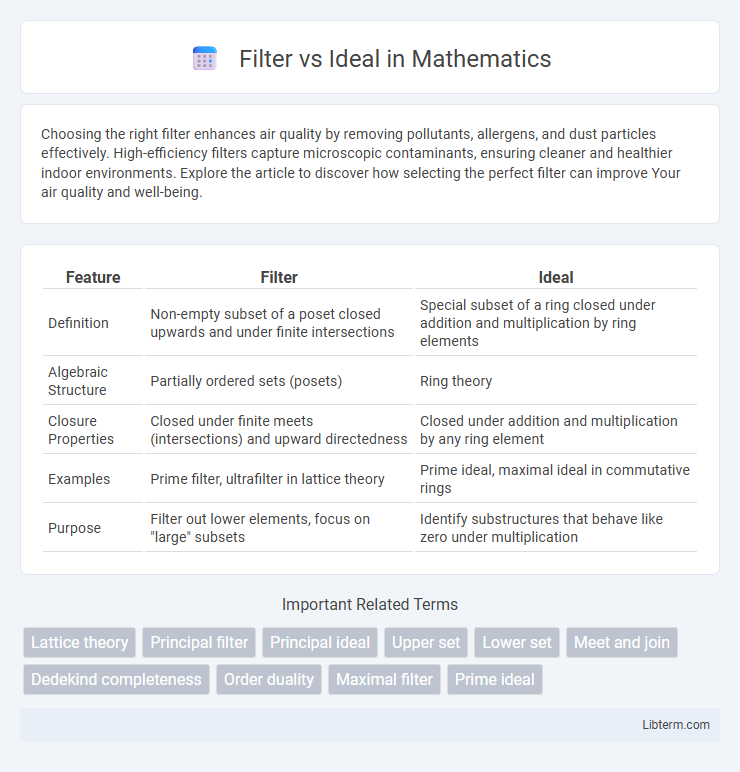
| Feature | Filter | Ideal |
|---|---|---|
| Definition | Non-empty subset of a poset closed upwards and under finite intersections | Special subset of a ring closed under addition and multiplication by ring elements |
| Algebraic Structure | Partially ordered sets (posets) | Ring theory |
| Closure Properties | Closed under finite meets (intersections) and upward directedness | Closed under addition and multiplication by any ring element |
| Examples | Prime filter, ultrafilter in lattice theory | Prime ideal, maximal ideal in commutative rings |
| Purpose | Filter out lower elements, focus on "large" subsets | Identify substructures that behave like zero under multiplication |
Introduction: Filter vs Ideal
Filter and Ideal represent two fundamental concepts in mathematics, particularly in order theory and lattice theory. A filter is a non-empty subset of a partially ordered set that is upward-closed and closed under finite intersection, used to generalize convergence and limit processes. In contrast, an ideal is a non-empty downward-closed subset closed under finite joins, often applied to structure the notion of approximation and decomposability within algebraic systems.
Defining Filters in Context
Defining filters in context involves specifying criteria that selectively process and refine data based on relevant attributes, ensuring targeted outcomes in various applications like search engines or data analysis. Filters operate by including or excluding information matching defined parameters, enhancing precision and efficiency. Ideal filters balance strictness and flexibility to optimize relevance without sacrificing necessary data diversity.
Understanding the Concept of Ideal
Ideal refers to a perfect or optimal standard that serves as a benchmark for comparison, embodying the most desirable qualities or outcomes in a given context. Understanding the concept of ideal involves recognizing its role as a theoretical model that guides decision-making, goal-setting, and problem-solving by highlighting what is best achievable. This contrasts with filter, which typically denotes a tool or method to selectively extract or refine data, emphasizing the ideal's broader, aspirational framework over practical selection processes.
Key Differences Between Filter and Ideal
Filter refers to a process or device that removes unwanted elements, such as impurities, particles, or noise, from a substance or signal, ensuring only desired components pass through. Ideal represents a perfect or optimal condition, standard, or model that is often unattainable, serving as a benchmark for comparison or aspiration. The key differences between filter and ideal lie in their functional roles; filter involves practical application and selective removal, while ideal embodies conceptual perfection without constraints or real-world limitations.
Real-World Applications of Filters
Filters play a crucial role in real-world applications by selectively allowing certain frequencies or signals to pass while attenuating others, critical in audio processing, telecommunications, and image enhancement. Unlike the theoretical Ideal filter, which has perfect frequency cutoff with no distortion or transition band, practical filters balance performance with physical constraints such as component tolerance and signal delay. Applications benefit from various filter types like low-pass, high-pass, band-pass, and notch filters to manage noise reduction, signal separation, and system stability in environments ranging from radio communications to biomedical devices.
Practical Uses of Ideals
Ideals are fundamental in ring theory for structuring and simplifying algebraic problems, serving as kernels for homomorphisms that enable the construction of quotient rings. Unlike filters, which are primarily used in lattice and order theory to generalize convergence and selection criteria, ideals have practical applications in solving polynomial equations and modular arithmetic. In computer algebra systems, ideals facilitate Groebner basis computations, enhancing algorithmic problem-solving in algebraic geometry and cryptography.
Filter vs Ideal: Mathematical Foundations
Filter and Ideal are fundamental concepts in order theory and algebra with distinct mathematical foundations. Filters on a poset are upward-closed and closed under finite meets, serving as structures to generalize notions of convergence and consistency. Ideals, conversely, are downward-closed and closed under finite joins, often representing generalized subsets or approximations within algebraic systems.
Advantages and Limitations of Filters
Filters offer practical advantages such as ease of implementation, cost-effectiveness, and suitability for real-time signal processing, making them ideal for noise reduction and data smoothing in various applications. Their limitations include potential distortion of signal characteristics and reduced accuracy in complex environments where ideal filter responses are unattainable. Ideal filters, while theoretically perfect with sharp cutoffs and no signal distortion, are impractical to implement due to infinite impulse response length and high computational demands.
The Role of Ideals in Algebraic Structures
Ideals serve as fundamental substructures within rings, facilitating the formation of quotient rings and enabling the analysis of algebraic properties through homomorphisms. Filters, typically used in order theory and lattice theory, help identify subsets with specific closure properties but do not directly contribute to ring quotients or factorization. The role of ideals in algebraic structures is pivotal for understanding divisibility, factorization, and module theory, distinguishing them from filters by their algebraic closure under ring operations.
Choosing Between Filter and Ideal: Which One to Use?
Choosing between Filter and Ideal depends on your specific application needs; Filter offers flexibility with real-time parameter adjustments and lower computational cost, making it suitable for dynamic systems and audio processing. Ideal filters provide perfect frequency separation with sharp cutoff but require high computational resources and cause phase distortion, better suited for offline analysis or scenarios demanding exact frequency isolation. Evaluating factors such as latency, implementation complexity, and desired filter characteristics guides the optimal choice between Filter and Ideal in signal processing tasks.
Filter Infographic
 libterm.com
libterm.com