The dot product is a fundamental operation in linear algebra that calculates the scalar result of two vectors' corresponding components multiplied and summed. It is widely used in computer graphics, physics, and machine learning to measure vector similarity and project one vector onto another. Explore the rest of the article to understand how the dot product can optimize your calculations and applications.
Table of Comparison
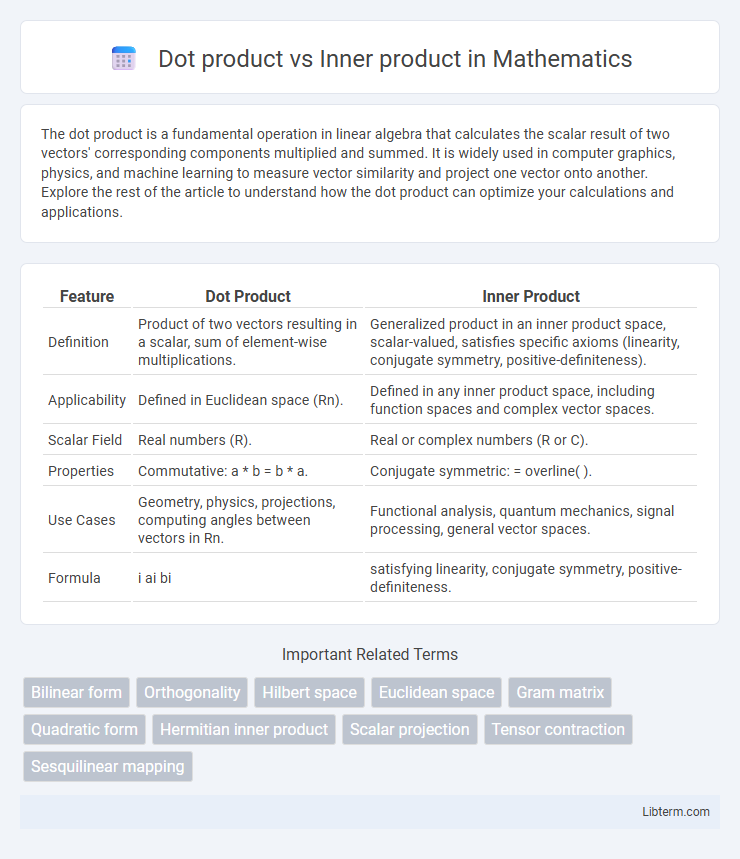
| Feature | Dot Product | Inner Product |
|---|---|---|
| Definition | Product of two vectors resulting in a scalar, sum of element-wise multiplications. | Generalized product in an inner product space, scalar-valued, satisfies specific axioms (linearity, conjugate symmetry, positive-definiteness). |
| Applicability | Defined in Euclidean space (Rn). | Defined in any inner product space, including function spaces and complex vector spaces. |
| Scalar Field | Real numbers (R). | Real or complex numbers (R or C). |
| Properties | Commutative: a * b = b * a. | Conjugate symmetric: |
| Use Cases | Geometry, physics, projections, computing angles between vectors in Rn. | Functional analysis, quantum mechanics, signal processing, general vector spaces. |
| Formula | i ai bi |
Introduction to Dot Product and Inner Product
The dot product is a specific type of inner product defined in Euclidean space where it calculates the sum of the products of corresponding vector components. Inner product generalizes this concept to abstract vector spaces, providing a way to measure angles and lengths through properties like linearity, symmetry, and positive-definiteness. Understanding the distinctions between dot product and inner product is essential for applications in linear algebra, functional analysis, and signal processing.
Mathematical Definitions
The dot product is a specific case of the inner product defined for Euclidean vectors in \(\mathbb{R}^n\), calculated as the sum of the products of corresponding components. An inner product generalizes this concept to abstract vector spaces with properties of linearity, symmetry (or conjugate symmetry), and positive-definiteness, enabling length and angle measurements. The dot product formula is \(\mathbf{a} \cdot \mathbf{b} = \sum_{i=1}^n a_i b_i\), while an inner product \(\langle x, y \rangle\) must satisfy axioms extending beyond Euclidean spaces.
Geometric Interpretations
The dot product measures the magnitude of projection of one vector onto another, yielding a scalar that represents the product of their magnitudes and the cosine of the angle between them. Inner product generalizes this concept to abstract vector spaces, defining an angle and length through a complex or real-valued function that satisfies linearity, symmetry, and positive definiteness. Geometrically, the dot product corresponds to the inner product in Euclidean space, enabling interpretation of orthogonality and vector length in both finite-dimensional and infinite-dimensional contexts.
Key Differences between Dot Product and Inner Product
The dot product specifically refers to the algebraic operation between two vectors in Euclidean space, yielding a scalar that measures their magnitude and directional alignment. The inner product generalizes this concept to abstract vector spaces, incorporating complex vectors and functions, and defining properties like linearity, conjugate symmetry, and positive-definiteness. Key differences include the dot product's restriction to real coordinate vectors and straightforward computation, whereas the inner product encompasses a broader range of spaces and structures, enabling advanced applications in functional analysis and quantum mechanics.
Applications in Vector Spaces
The dot product is a specific case of the inner product defined in Euclidean vector spaces, used extensively in physics for work calculation and projection of vectors. Inner products generalize the dot product to complex vector spaces, enabling applications in quantum mechanics, signal processing, and functional analysis where notions of length and angle must be preserved. Both operators facilitate orthogonality testing, vector norm computation, and form the foundation for algorithms in machine learning and computer graphics.
Properties and Axioms
The dot product is a specific example of an inner product defined in Euclidean space, characterized by properties such as linearity, symmetry, and positive-definiteness. Inner products generalize the dot product to abstract vector spaces and must satisfy axioms including conjugate symmetry (in complex spaces), linearity in the first argument, and positive-definiteness to induce a norm. Both operations enable the definition of angles and lengths in their respective spaces but differ in applicability depending on the underlying field and vector space structure.
Use Cases in Physics and Engineering
The dot product, a specific case of the inner product for Euclidean spaces, is widely used in physics and engineering to calculate work done by a force and to determine projections of vectors. Inner products generalize this concept to abstract vector spaces, enabling applications such as quantum state overlaps in quantum mechanics and signal correlation in electrical engineering. Understanding the scope of inner products facilitates advanced analyses in functional spaces beyond the geometric interpretations of dot products.
Generalization to Higher Dimensions
The dot product, specializing in Euclidean spaces, computes the sum of pairwise products of vector components, typically in two or three dimensions. The inner product generalizes this concept to higher-dimensional and abstract vector spaces by defining a bilinear, symmetric, positive-definite form that satisfies specific axioms. This generalization enables the extension of geometric notions like length and angle to infinite-dimensional spaces, essential in functional analysis and quantum mechanics.
Common Misconceptions
The dot product is often confused with the inner product, but the dot product specifically refers to the inner product in Euclidean space using the standard basis. Many mistakenly assume all inner products follow the dot product formula, overlooking that inner products can vary in different vector spaces with distinct definitions and properties. Understanding that the inner product generalizes the dot product is crucial for accurate application in abstract vector spaces and functional analysis.
Summary and Conclusion
The dot product is a specific type of inner product defined in Euclidean space, calculated as the sum of the products of corresponding vector components. Inner products generalize this concept to abstract vector spaces, allowing definitions of length and angle beyond Euclidean geometry. Understanding the dot product as a subset of inner products highlights its role in measuring projections and similarities within both practical applications and theoretical frameworks.
Dot product Infographic
 libterm.com
libterm.com