Fiber bundles are a fundamental concept in topology and differential geometry, providing a structured way to understand how spaces locally resemble a product of two spaces but may have a different global structure. They consist of a base space, a total space, and a projection map that connects the fibers to each point of the base. Explore this article to learn how fiber bundles play a crucial role in fields like physics and mathematics, enriching your grasp of complex spatial relationships.
Table of Comparison
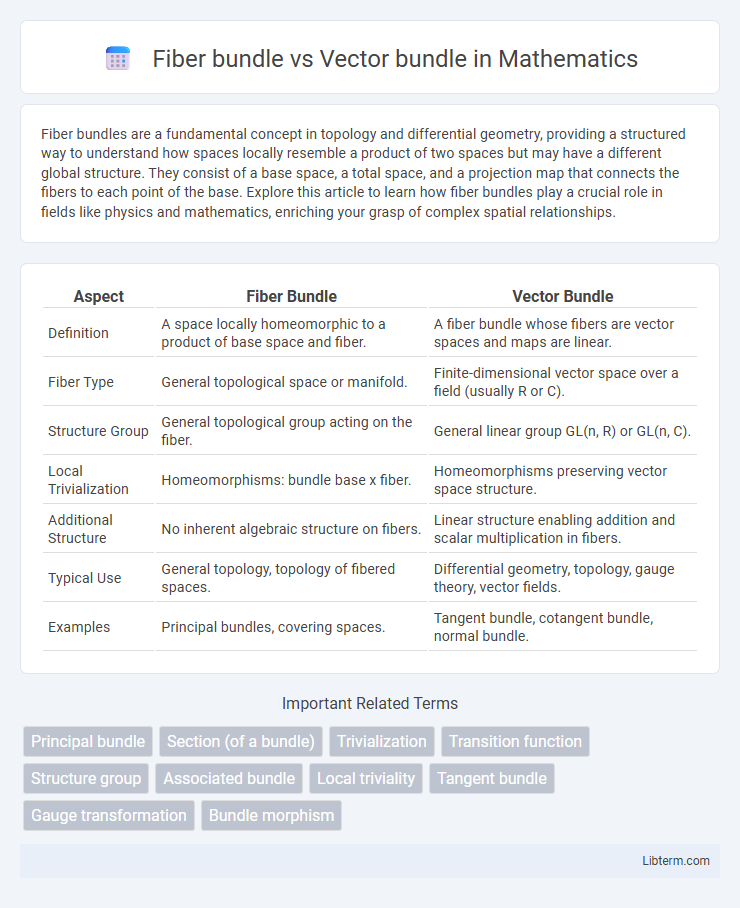
| Aspect | Fiber Bundle | Vector Bundle |
|---|---|---|
| Definition | A space locally homeomorphic to a product of base space and fiber. | A fiber bundle whose fibers are vector spaces and maps are linear. |
| Fiber Type | General topological space or manifold. | Finite-dimensional vector space over a field (usually R or C). |
| Structure Group | General topological group acting on the fiber. | General linear group GL(n, R) or GL(n, C). |
| Local Trivialization | Homeomorphisms: bundle base x fiber. | Homeomorphisms preserving vector space structure. |
| Additional Structure | No inherent algebraic structure on fibers. | Linear structure enabling addition and scalar multiplication in fibers. |
| Typical Use | General topology, topology of fibered spaces. | Differential geometry, topology, gauge theory, vector fields. |
| Examples | Principal bundles, covering spaces. | Tangent bundle, cotangent bundle, normal bundle. |
Introduction to Bundles in Mathematics
Fiber bundles and vector bundles are fundamental constructs in differential geometry and topology, serving as tools to study spaces locally resembling a product space. A fiber bundle consists of a base space, a total space, and a projection mapping with fibers homeomorphic to a typical fiber space; vector bundles specifically have fibers that are vector spaces, preserving linear structure across local trivializations. These bundles facilitate analysis of manifold structures, enabling applications in gauge theory, characteristic classes, and complex geometry by encoding local-to-global properties.
Definitions: What Is a Fiber Bundle?
A fiber bundle is a topological space that locally resembles a product space, consisting of a base space, a total space, and a typical fiber, connected by a continuous surjective projection map. Each point in the base space has a neighborhood where the preimage under the projection is homeomorphic to the product of that neighborhood and the fiber. Vector bundles are special cases of fiber bundles where the fiber is a vector space, and the transition maps preserve the vector space structure.
Understanding Vector Bundles
Vector bundles are a special class of fiber bundles where each fiber is a vector space, enabling linear algebraic operations to be performed fiberwise. Unlike general fiber bundles, which may have arbitrary topological spaces as fibers, vector bundles require the fibers to be vector spaces of fixed dimension, ensuring smoothness and compatibility with linear structures. Understanding vector bundles is fundamental in differential geometry and topology because they provide the framework for studying sections, connections, and curvature in a linear setting.
Key Differences Between Fiber Bundles and Vector Bundles
Fiber bundles are topological spaces locally homeomorphic to a product space with a fixed fiber type, whereas vector bundles specifically have fibers that are vector spaces with linear structure. Vector bundles require transition functions to be linear isomorphisms between fibers, ensuring compatibility with vector space operations, while fiber bundles have more general fibers without such algebraic constraints. The primary distinction lies in the algebraic structure on the fibers, making vector bundles a specialized subclass of fiber bundles with linearity conditions.
Structure Groups and Typical Fibers
Fiber bundles are defined by a structure group acting continuously on the typical fiber, which is a topological space representing the local model of the bundle, while vector bundles specifically have a structure group as a general linear group GL(n, R) or GL(n, C) acting linearly on a typical fiber that is a vector space. The structure group in a fiber bundle dictates the transition functions and the local trivializations preserving the fiber's topological structure, whereas in vector bundles, the structure group maintains the linear structure of the fibers and enables operations like vector addition and scalar multiplication. Typical fibers in fiber bundles can be any space, often manifolds or algebraic varieties, but in vector bundles, the typical fiber is always a finite-dimensional vector space, ensuring linearity in the bundle.
Examples of Fiber Bundles in Topology
The Mobius strip serves as a classical example of a fiber bundle with fiber being a line segment and the base space a circle, illustrating a non-trivial bundle with a twist. Another prominent example is the Hopf fibration, where the 3-sphere fibers over the 2-sphere with fiber a circle, demonstrating a principal bundle crucial in algebraic topology. Vector bundles, such as the tangent bundle of a manifold, differ by having fibers modeled on vector spaces, whereas fiber bundles can have more general fiber structures and are essential to understanding continuous mappings in topology.
Common Vector Bundle Applications
Vector bundles serve as fundamental structures in differential geometry, enabling the analysis of tangent spaces, cotangent spaces, and tensor fields on manifolds. Fiber bundles provide a more general framework, but vector bundles specifically support sections that represent vector fields, facilitating applications in gauge theory, fiber bundle connections, and complex geometry. Common vector bundle applications include modeling physical fields in theoretical physics, studying moduli spaces in algebraic geometry, and constructing vector bundles over Riemann surfaces for advanced topological insights.
Local Triviality and Transition Functions
Fiber bundles and vector bundles both exhibit local triviality, meaning each bundle locally resembles a product space of a base and a typical fiber; however, vector bundles specifically have fibers that are vector spaces with linear transition functions. Transition functions in fiber bundles are homeomorphisms between fibers on overlapping neighborhoods, preserving fiber structure, whereas in vector bundles these functions are linear isomorphisms maintaining vector space operations. The distinction in transition functions reflects the algebraic structure inherent in vector bundles, facilitating applications in differential geometry and topology where linearity is essential.
Characteristic Classes: Distinguishing the Bundles
Characteristic classes serve as powerful invariants to distinguish fiber bundles from vector bundles by capturing topological features of their structure groups and total spaces. Vector bundles have well-studied characteristic classes such as Chern classes, Stiefel-Whitney classes, and Pontryagin classes, which reflect the algebraic structure of associated vector spaces, while general fiber bundles may lack these specific classes due to more general fibers. The computation and comparison of these characteristic classes enable mathematicians to identify the nature of a bundle and detect differences in topology and geometry between fiber and vector bundles.
Conclusion: Choosing Between Fiber and Vector Bundles
Fiber bundles provide a general framework situating complex topological spaces locally resembling a fiber connected to a base space, whereas vector bundles specialize this concept by imposing linear structure on fibers, facilitating algebraic and geometric analyses. Selecting between fiber bundles and vector bundles depends largely on the problem's requirements for linearity, smoothness, and algebraic operations; vector bundles excel in contexts requiring linear algebraic manipulations, such as in differential geometry and gauge theory. Fiber bundles offer greater flexibility in diverse topological applications without inherent linear constraints, making them ideal for broader structural modeling beyond vector space frameworks.
Fiber bundle Infographic
 libterm.com
libterm.com