A branch point is a crucial site within RNA splicing where the lariat structure forms to facilitate intron removal during mRNA processing. This conserved nucleotide plays a pivotal role in ensuring accurate gene expression by guiding the spliceosome machinery. Explore the rest of the article to understand how branch points influence genetic regulation and splicing mechanisms.
Table of Comparison
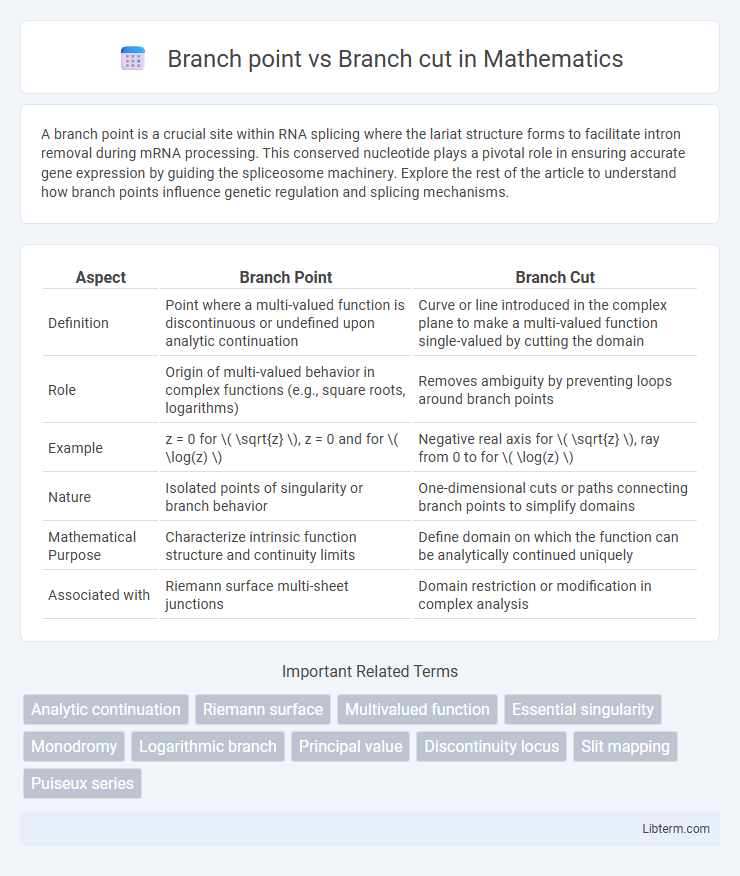
| Aspect | Branch Point | Branch Cut |
|---|---|---|
| Definition | Point where a multi-valued function is discontinuous or undefined upon analytic continuation | Curve or line introduced in the complex plane to make a multi-valued function single-valued by cutting the domain |
| Role | Origin of multi-valued behavior in complex functions (e.g., square roots, logarithms) | Removes ambiguity by preventing loops around branch points |
| Example | z = 0 for \( \sqrt{z} \), z = 0 and for \( \log(z) \) | Negative real axis for \( \sqrt{z} \), ray from 0 to for \( \log(z) \) |
| Nature | Isolated points of singularity or branch behavior | One-dimensional cuts or paths connecting branch points to simplify domains |
| Mathematical Purpose | Characterize intrinsic function structure and continuity limits | Define domain on which the function can be analytically continued uniquely |
| Associated with | Riemann surface multi-sheet junctions | Domain restriction or modification in complex analysis |
Introduction to Branch Points and Branch Cuts
Branch points and branch cuts are fundamental concepts in complex analysis used to handle multi-valued functions such as the complex logarithm or square root. A branch point is a location in the complex plane where a function is discontinuous upon analytic continuation around that point, causing the function value to change after encircling it. Branch cuts are carefully chosen curves extending from branch points that define single-valued branches of a multi-valued function by restricting the domain and preventing encirclement of branch points.
The Concept of Multi-Valued Functions
Branch points are specific points in the complex plane where a multi-valued function, such as the complex logarithm or the square root, fails to be single-valued and causes the function's values to cycle through different branches. Branch cuts are curves or lines introduced to remove ambiguity by defining a domain where the function is single-valued, effectively "cutting" the complex plane to restrict continuity across multiple branches. Understanding the interplay between branch points and branch cuts is essential for analyzing multi-valued functions and ensuring well-defined analytic continuations.
Defining Branch Points in Complex Analysis
Branch points in complex analysis are points where a multi-valued function, such as the complex logarithm or root functions, fails to be analytic and where the function's values cycle through different branches upon encircling these points. Unlike branch cuts, which are chosen curves or lines that restrict the domain to create a single-valued branch, branch points are intrinsic singularities where the function's multi-valued nature originates. Defining branch points involves identifying these critical points in the complex plane, often associated with the zeros of the function argument inside fractional powers or points causing discontinuity in the argument of logarithms.
Understanding Branch Cuts and Their Purpose
Branch cuts are crucial in complex analysis to define single-valued branches of multi-valued functions like the complex logarithm or square root, preventing ambiguity around branch points where functions become discontinuous. A branch point is a point on the complex plane at which a multi-valued function is not analytically continuous when encircling it, whereas the branch cut is a curve or line drawn from the branch point to restrict the domain and make the function single-valued. By strategically placing branch cuts, mathematically consistent and well-defined function values are achieved across the complex plane, enabling accurate evaluations and integrals in complex analysis.
Types of Branch Points: Algebraic and Logarithmic
Branch points arise in complex analysis where multi-valued functions like roots or logarithms fail to be single-valued; algebraic branch points occur when functions like z^(1/n) loop through n different values around the point. Logarithmic branch points appear in functions involving the logarithm, where circling the point changes the function value by 2pi, creating infinitely many branches. Understanding the nature of algebraic versus logarithmic branch points helps define appropriate branch cuts to produce single-valued branches of these complex functions.
Common Examples: Square Root and Logarithm Functions
Branch points occur where multi-valued functions like the square root and logarithm become discontinuous or undefined, often at points such as zero for the square root and zero or negative real axis for the logarithm. Branch cuts are chosen paths or curves on the complex plane that prevent crossing these discontinuities, typically the negative real axis for the logarithm function and the non-positive real axis for the square root function. These branch cuts enable the definition of a single-valued branch of the function by restricting the domain and avoiding the ambiguity caused by the multi-valued nature at branch points.
How to Choose Branch Cuts in Practice
Choosing branch cuts in practice involves selecting lines or curves in the complex plane where a multi-valued function, such as the complex logarithm or square root, is discontinuous to define a single-valued branch. The branch cut must exclude the branch point, which is a singularity where the function fails to be analytic, ensuring the function remains continuous elsewhere. Commonly, branch cuts are placed along rays extending from branch points to infinity or between branch points to simplify integration paths and maintain consistency in complex analysis applications.
Visualizing Branch Points and Branch Cuts on the Complex Plane
Branch points in complex analysis denote locations where a multi-valued function's values cycle upon encircling the point, often visualized as punctures or singularities on the complex plane. Branch cuts are curves or lines introduced to create a single-valued function by connecting branch points, typically shown as segments that prevent looping around these points. Visualizing these elements involves plotting branch cuts as rays or contours extending from branch points, highlighting discontinuities that enforce a unique function determination on the complex domain.
Applications of Branch Points and Cuts in Mathematics and Physics
Branch points and branch cuts are essential in complex analysis for defining multi-valued functions like logarithms and square roots, enabling the construction of single-valued branches crucial for contour integration and analytic continuation. In physics, branch cuts represent discontinuities across Riemann surfaces, facilitating the study of quantum field theory propagators, wave function singularities, and phase transitions in statistical mechanics. Applications in string theory and fluid dynamics also rely on branch points to describe multivalued potentials and complex flow patterns, providing a robust framework for solving nonlinear differential equations and modeling phenomena with intrinsic topological complexity.
Summary and Key Differences Between Branch Points and Branch Cuts
Branch points are singular points in complex functions where the function values become multi-valued, causing ambiguity in function determination around these points. Branch cuts are carefully chosen lines or curves in the complex plane introduced to make multi-valued functions single-valued by restricting the domain and effectively "cutting" the plane to avoid loops around branch points. The key difference lies in their roles: branch points mark the locations of multi-valued behavior, while branch cuts define the continuous paths that prevent encircling those points to maintain consistent function values.
Branch point Infographic
 libterm.com
libterm.com