The fundamental group is a key concept in algebraic topology that captures the idea of loops in a space and how they can be continuously transformed into one another. This group reflects the topological structure of the space and helps classify spaces based on their shape. Discover how the fundamental group reveals deep insights into your study of topological spaces by reading the rest of this article.
Table of Comparison
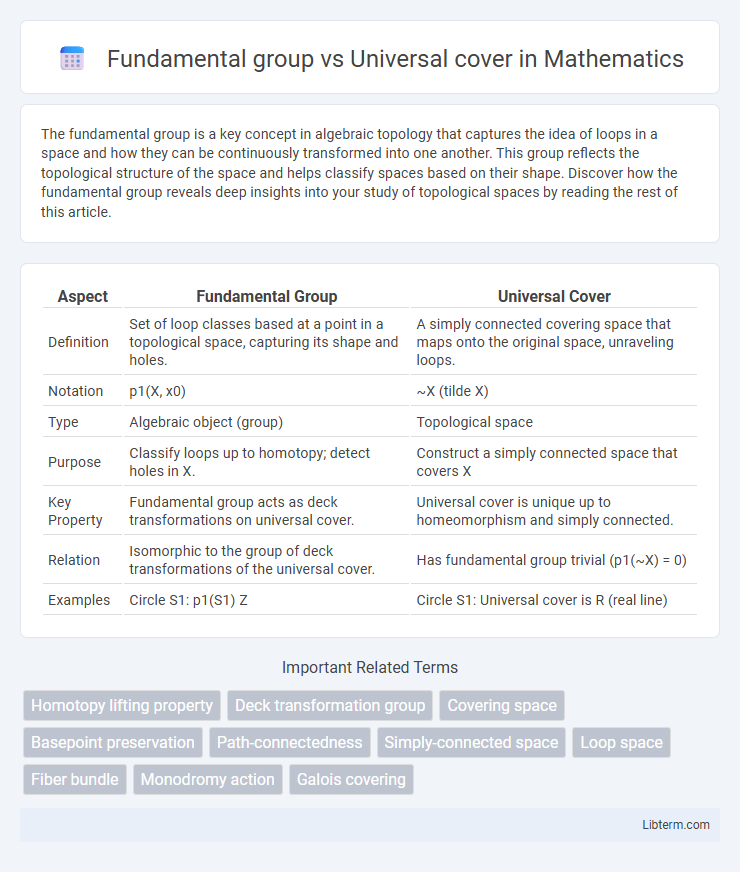
| Aspect | Fundamental Group | Universal Cover |
|---|---|---|
| Definition | Set of loop classes based at a point in a topological space, capturing its shape and holes. | A simply connected covering space that maps onto the original space, unraveling loops. |
| Notation | p1(X, x0) | ~X (tilde X) |
| Type | Algebraic object (group) | Topological space |
| Purpose | Classify loops up to homotopy; detect holes in X. | Construct a simply connected space that covers X |
| Key Property | Fundamental group acts as deck transformations on universal cover. | Universal cover is unique up to homeomorphism and simply connected. |
| Relation | Isomorphic to the group of deck transformations of the universal cover. | Has fundamental group trivial (p1(~X) = 0) |
| Examples | Circle S1: p1(S1) Z | Circle S1: Universal cover is R (real line) |
Introduction to Fundamental Groups and Universal Covers
The fundamental group captures the loop-based structure of a topological space by classifying loops up to homotopy, revealing key information about the space's shape and connectivity. Universal covers provide simply connected spaces that map onto the original space, serving as a tool to study the fundamental group through covering maps and deck transformations. Understanding the interplay between fundamental groups and universal covers is essential for analyzing the topological and algebraic properties of spaces.
Defining the Fundamental Group: Concepts and Examples
The fundamental group, denoted p1(X, x0), is defined as the set of equivalence classes of loops based at a point x0 in a topological space X, where loops are identified up to continuous deformation called homotopy. This group captures the essential "hole structure" of the space, serving as a key algebraic invariant in algebraic topology. For example, the fundamental group of the circle S1 is isomorphic to the integers Z, representing how many times loops wind around the circle.
Understanding Universal Covering Spaces
Universal covering spaces provide a simply connected space that maps onto a given topological space, allowing the fundamental group to act as the deck transformation group controlling the covering's symmetry. The fundamental group captures the loops in the base space up to homotopy, while the universal cover unravels these loops into unique paths without loops. This correspondence facilitates algebraic analysis of topological spaces by translating complex loop structures into the simpler topology of the universal cover.
The Relationship Between Fundamental Group and Universal Cover
The fundamental group classifies loops in a topological space, measuring its essential "holes" via homotopy classes based at a point. The universal cover is a simply connected space that covers the original space, unwinding all loops corresponding to nontrivial elements in the fundamental group. This relationship establishes a correspondence where the fundamental group acts as the group of deck transformations of the universal cover, encoding the space's loop structure through symmetry operations on the cover.
Fundamental Group: Algebraic Properties
The fundamental group, denoted p1(X, x0), encodes the algebraic structure of loops based at a point x0 in a topological space X, capturing essential information about the space's path-connectedness and hole structure. It is a group under the operation of path concatenation up to homotopy, reflecting key algebraic properties such as being finitely generated or free in many important cases. This group serves as a primary invariant in algebraic topology, with its properties determining the existence and structure of universal covers, where the fundamental group acts as the deck transformation group of the covering space.
Universal Cover: Topological Characteristics
The universal cover of a topological space is a simply connected covering space that maps onto the original space via a continuous surjective map, preserving local homeomorphisms. Its topological characteristics include having a trivial fundamental group, reflecting the fact that loops in the base space can be lifted to paths in the universal cover without forming nontrivial loops. This construction reveals the structure of the fundamental group of the base space as the group of deck transformations acting freely and properly discontinuously on the universal cover.
Classification of Spaces via Fundamental Group
The fundamental group serves as a key algebraic invariant classifying topological spaces based on their loop structures and homotopy classes, encapsulating essential information about space connectivity. Universal covers provide simply connected covering spaces corresponding to the fundamental group, enabling the study of space properties through lifting loops and paths. This interplay between fundamental groups and universal covers underpins the classification of spaces, where different fundamental groups correspond to distinct universal covers, allowing topologists to distinguish and categorize spaces up to homotopy equivalence.
Key Applications in Topology and Geometry
The fundamental group captures essential information about a space's loop structures and classifies its covering spaces, serving as a critical tool in algebraic topology for distinguishing topological spaces up to homotopy. The universal cover provides a simply connected space that maps onto the original space, allowing complex spaces to be studied through their simpler universal covers, which simplifies computations in homology and homotopy. Applications include analyzing manifold structures, classifying fiber bundles, and solving problems related to curvature and geometric group theory by linking algebraic properties of the fundamental group with geometric features of the universal cover.
Common Misconceptions and Pitfalls
The fundamental group classifies loops based at a point in a topological space, while the universal cover is a simply connected space that maps onto the original space via a covering map. A common misconception is that the universal cover is always unique up to homeomorphism, but it is unique only up to isomorphism of covering spaces preserving basepoints. Another pitfall is confusing the completeness of the universal cover with the triviality of the fundamental group; the universal cover is simply connected, but a trivial fundamental group implies the space itself is already simply connected.
Conclusion: Insights and Open Questions
The fundamental group captures the intrinsic loop structure of a space, while the universal cover provides a simply connected space that unravels this complexity, establishing a powerful duality in algebraic topology. Insights reveal that the universal cover acts as a principal bundle with the fundamental group as its deck transformation group, bridging geometry and algebra. Open questions center on characterizing universal covers in more complex spaces and understanding the interplay between higher homotopy groups and generalized covering spaces.
Fundamental group Infographic
 libterm.com
libterm.com