Deductive reasoning starts with a general statement or hypothesis and examines the possibilities to reach a specific, logical conclusion. This method is widely used in fields such as mathematics, science, and law to ensure precise decision-making based on established facts. Discover how mastering deductive techniques can enhance your critical thinking skills by reading the rest of the article.
Table of Comparison
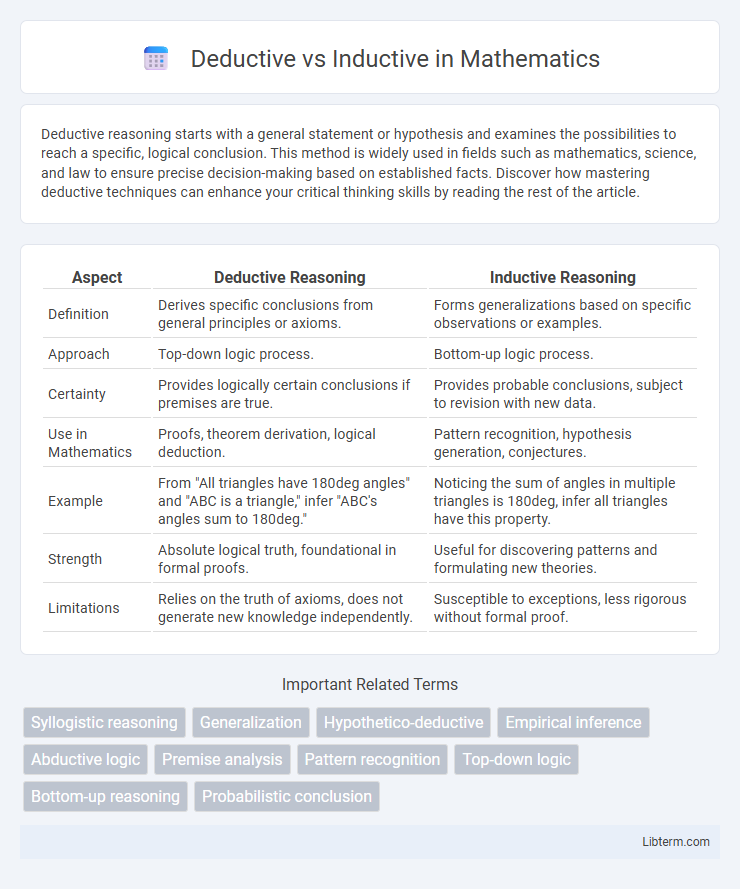
| Aspect | Deductive Reasoning | Inductive Reasoning |
|---|---|---|
| Definition | Derives specific conclusions from general principles or axioms. | Forms generalizations based on specific observations or examples. |
| Approach | Top-down logic process. | Bottom-up logic process. |
| Certainty | Provides logically certain conclusions if premises are true. | Provides probable conclusions, subject to revision with new data. |
| Use in Mathematics | Proofs, theorem derivation, logical deduction. | Pattern recognition, hypothesis generation, conjectures. |
| Example | From "All triangles have 180deg angles" and "ABC is a triangle," infer "ABC's angles sum to 180deg." | Noticing the sum of angles in multiple triangles is 180deg, infer all triangles have this property. |
| Strength | Absolute logical truth, foundational in formal proofs. | Useful for discovering patterns and formulating new theories. |
| Limitations | Relies on the truth of axioms, does not generate new knowledge independently. | Susceptible to exceptions, less rigorous without formal proof. |
Understanding Deductive and Inductive Reasoning
Deductive reasoning involves drawing specific conclusions from general premises, ensuring certainty if the premises are true, which is fundamental in formal logic and mathematics. Inductive reasoning, conversely, derives generalized conclusions from specific observations, providing probabilistic rather than definitive outcomes, commonly used in scientific research and hypothesis formation. Mastery of deductive and inductive reasoning enhances critical thinking by enabling accurate evaluation of arguments and evidence in various disciplines.
Key Differences Between Deductive and Inductive Approaches
Deductive reasoning starts with a general theory or hypothesis and tests it through specific observations, ensuring conclusions are logically certain if premises are true. Inductive reasoning, conversely, begins with detailed observations and formulates broader generalizations or theories, offering probabilistic conclusions that can be revised with new data. Key differences include directionality--deductive moves from general to specific, while inductive moves from specific to general--and certainty of conclusions, with deductive providing definitive proof and inductive providing likelihood based on evidence.
Characteristics of Deductive Reasoning
Deductive reasoning starts with a general premise or theory and moves toward a specific conclusion, ensuring that if the premises are true, the conclusion must be true. It is characterized by its logical certainty, structured process, and reliance on established facts or principles. This method is often used in formal logic, mathematics, and scientific proofs to derive valid conclusions from given premises.
Characteristics of Inductive Reasoning
Inductive reasoning involves deriving general principles from specific observations, emphasizing probability rather than certainty. It advances knowledge by identifying patterns, forming hypotheses, and making predictions based on limited data sets. This reasoning is inherently open to revision as new evidence emerges, reflecting its foundation in empirical observation and flexibility.
Examples of Deductive Reasoning in Practice
Deductive reasoning is commonly applied in mathematics, where general principles such as the laws of arithmetic lead to specific conclusions like solving for unknown variables in equations. In legal contexts, deductive reasoning interprets statutes by applying broad legal rules to particular cases, ensuring consistent judgments. Scientific experiments use deductive logic by starting from established theories and deriving hypotheses that predict specific measurable outcomes.
Examples of Inductive Reasoning in Everyday Life
Inductive reasoning in everyday life includes observing that the sun rises every morning and concluding it will rise tomorrow, or noticing that a friend has been late to several meetings and predicting they might be late again. Another common example is tasting a new fruit and finding it sweet, leading to the assumption that other similar fruits will also taste sweet. These instances illustrate how specific observations form the basis for general conclusions through inductive logic.
Strengths and Limitations of Deductive Methods
Deductive methods excel in providing logically certain conclusions when premises are true, making them highly reliable for testing hypotheses in scientific research. Their structured approach enables clear validation or falsification of theories but limits flexibility, as they rely heavily on the accuracy of initial assumptions. A major limitation is their inability to generate new knowledge beyond the given premises, restricting innovation to the scope of existing frameworks.
Strengths and Limitations of Inductive Methods
Inductive methods excel at generating new hypotheses and theories by analyzing patterns and specific observations, making them valuable for exploratory research and situations with limited prior knowledge. Their strength lies in flexibility and adaptability, allowing for the discovery of complex relationships without predefined frameworks. However, inductive approaches face limitations in establishing definitive conclusions, as findings may be prone to bias, overgeneralization, and lack of replicability compared to deductive methods.
When to Use Deductive vs Inductive Reasoning
Deductive reasoning is best used when applying general principles to reach a specific conclusion, ideal for situations requiring certainty and logical proof, such as mathematical proofs or legal arguments. Inductive reasoning suits scenarios where patterns or evidence are used to form generalizations, often applied in scientific research, hypothesis generation, and decision-making under uncertainty. Use deductive reasoning when the goal is to test a theory or rule, and use inductive reasoning when exploring data to develop new theories or predictions.
Deductive and Inductive Reasoning: Which is Better?
Deductive reasoning starts with general principles and moves towards specific conclusions, ensuring conclusions are logically certain if premises are true. Inductive reasoning, by contrast, derives generalizations from specific observations, providing probable but not guaranteed conclusions. Choosing between deductive and inductive reasoning depends on context; deductive reasoning excels in formal logic and mathematics, while inductive reasoning is essential for scientific discovery and hypothesis formation.
Deductive Infographic
 libterm.com
libterm.com