Functional analysis explores mathematical functions and their properties within spaces, focusing on concepts such as normed vector spaces, linear operators, and convergence. This branch of mathematics underpins many applications in differential equations, quantum mechanics, and optimization problems. Discover more about how functional analysis can deepen your understanding of complex systems in the full article.
Table of Comparison
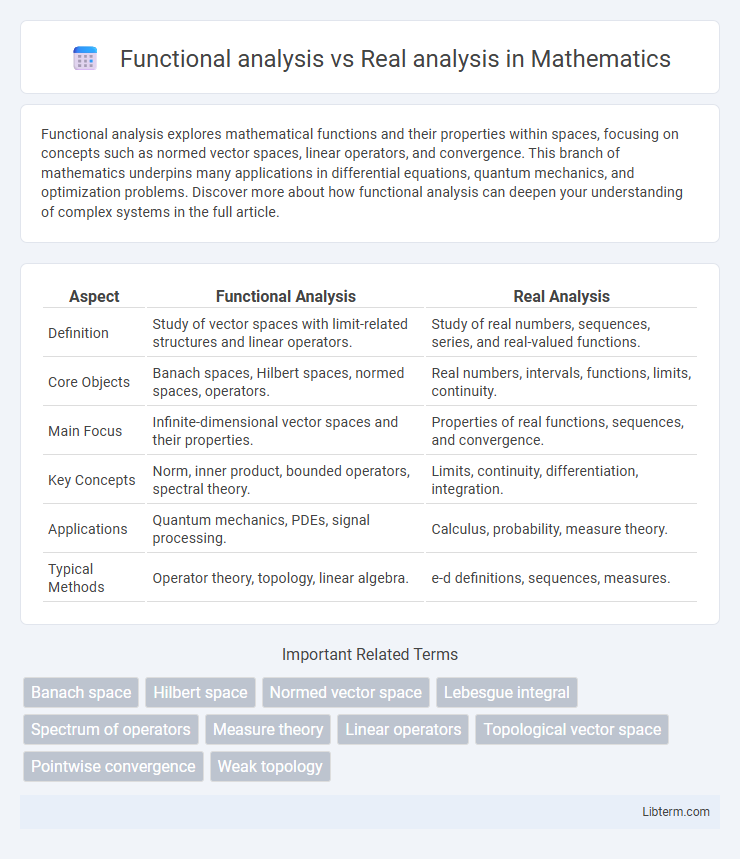
| Aspect | Functional Analysis | Real Analysis |
|---|---|---|
| Definition | Study of vector spaces with limit-related structures and linear operators. | Study of real numbers, sequences, series, and real-valued functions. |
| Core Objects | Banach spaces, Hilbert spaces, normed spaces, operators. | Real numbers, intervals, functions, limits, continuity. |
| Main Focus | Infinite-dimensional vector spaces and their properties. | Properties of real functions, sequences, and convergence. |
| Key Concepts | Norm, inner product, bounded operators, spectral theory. | Limits, continuity, differentiation, integration. |
| Applications | Quantum mechanics, PDEs, signal processing. | Calculus, probability, measure theory. |
| Typical Methods | Operator theory, topology, linear algebra. | e-d definitions, sequences, measures. |
Introduction to Functional Analysis and Real Analysis
Functional analysis explores infinite-dimensional vector spaces through the study of normed spaces, Banach spaces, and Hilbert spaces, emphasizing operators acting on these spaces. Real analysis focuses on the rigorous examination of real numbers, sequences, series, continuity, differentiation, and integration on the real line, providing the foundational underpinnings for calculus. Both fields intersect in examining convergence and continuity, but functional analysis extends these concepts to abstract spaces and linear operators.
Core Concepts in Functional Analysis
Functional analysis centers on the study of vector spaces endowed with a topology, particularly Banach and Hilbert spaces, along with continuous linear operators acting on them. Core concepts include norms, inner products, compact operators, spectral theory, and fixed-point theorems, which provide critical tools for solving differential and integral equations. Real analysis primarily investigates properties of real-valued functions, limits, continuity, differentiation, and integration in the context of the real number line or Euclidean spaces.
Key Principles of Real Analysis
Real analysis centers on the rigorous study of limits, continuity, differentiation, and integration within the realm of real numbers, emphasizing epsilon-delta definitions and properties of real-valued functions. It investigates sequences, series, and measure theory, establishing foundational principles such as completeness, compactness, and connectedness in metric spaces. In contrast, functional analysis extends these concepts to infinite-dimensional vector spaces and operators, focusing on normed spaces, Banach and Hilbert spaces, and linear transformations.
Historical Evolution and Development
Functional analysis emerged in the early 20th century, rooted in the study of function spaces and operators, building on foundational concepts from real analysis established by mathematicians like Cauchy and Weierstrass in the 19th century. Real analysis provided rigorous definitions of limits, continuity, and integration, laying the groundwork for functional analysis to explore infinite-dimensional vector spaces and linear operators. The development of Banach and Hilbert spaces in the 1920s marked a significant advance, bridging the gap between abstract algebraic structures and classical analysis techniques.
Major Differences Between Functional and Real Analysis
Functional analysis primarily studies infinite-dimensional vector spaces and operators acting upon them, emphasizing spaces such as Hilbert and Banach spaces. Real analysis focuses on properties of real numbers, sequences, series, and functions of real variables, emphasizing limits, continuity, and integration. The major difference lies in functional analysis addressing abstract spaces and linear transformations, whereas real analysis deals with the rigorous foundations of calculus on real number domains.
Applications of Functional Analysis in Mathematics and Science
Functional analysis, a branch of mathematical analysis dealing with function spaces and linear operators, plays a crucial role in solving differential equations, quantum mechanics, and signal processing. Its application in optimization theory and control systems aids in modeling and analyzing complex physical and engineering phenomena. Real analysis focuses more on the properties of real-valued functions and sequences, providing foundational tools, while functional analysis extends these concepts to infinite-dimensional vector spaces for advanced applications.
Uses of Real Analysis Across Disciplines
Real analysis provides the foundational tools for calculus and measure theory, making it essential in fields such as economics for optimization problems, physics for understanding continuous phenomena, and computer science for algorithms involving limits and continuity. This branch of mathematics enables precise modeling of real-world systems by studying functions, sequences, and series, which are crucial in statistical mechanics, engineering, and quantitative finance. Functional analysis extends real analysis concepts into infinite-dimensional spaces and is widely used in quantum mechanics, signal processing, and solving differential equations.
Overlapping Areas and Connections
Functional analysis and real analysis intersect primarily in the study of sequences, series, and functions of real variables within complete normed vector spaces, such as Banach and Hilbert spaces. Concepts like measure theory, L^p spaces, and convergence theorems form foundational overlaps that facilitate rigorous treatment of functional limits, continuity, and integrability. These connections enable extensions of real analysis principles to infinite-dimensional settings, enhancing tools for solving differential equations and optimization problems.
Choosing the Right Field: Functional or Real Analysis
Choosing between functional analysis and real analysis depends on your mathematical focus and applications; functional analysis emphasizes infinite-dimensional vector spaces and operator theory crucial for quantum mechanics and PDEs, while real analysis deals with properties of real numbers, sequences, and functions foundational to calculus and measure theory. Functional analysis provides tools to analyze functions and transformations in abstract spaces, making it essential for advanced studies in applied mathematics and physics, whereas real analysis offers rigorous groundwork for understanding continuity, limits, and integration. Your choice should align with whether your interest lies in abstract structures and linear operators or in detailed properties of real-valued functions and sequences.
Future Directions and Trends
Functional analysis is increasingly influencing machine learning and quantum computing through the study of infinite-dimensional vector spaces and operator theory, highlighting its growing role in data science innovations. Real analysis continues to advance in measure theory and integration techniques, supporting developments in stochastic processes and financial modeling. Future trends indicate a convergence of both fields with applied mathematics and computational methods to address complex problems in physics, economics, and engineering.
Functional analysis Infographic
 libterm.com
libterm.com