Algebraic surfaces are geometric objects defined by polynomial equations in three variables, exhibiting complex structures and rich mathematical properties. Understanding these surfaces reveals insights into areas such as topology, complex analysis, and algebraic geometry, with applications spanning computer graphics to theoretical physics. Explore the rest of the article to deepen your knowledge of algebraic surfaces and their fascinating characteristics.
Table of Comparison
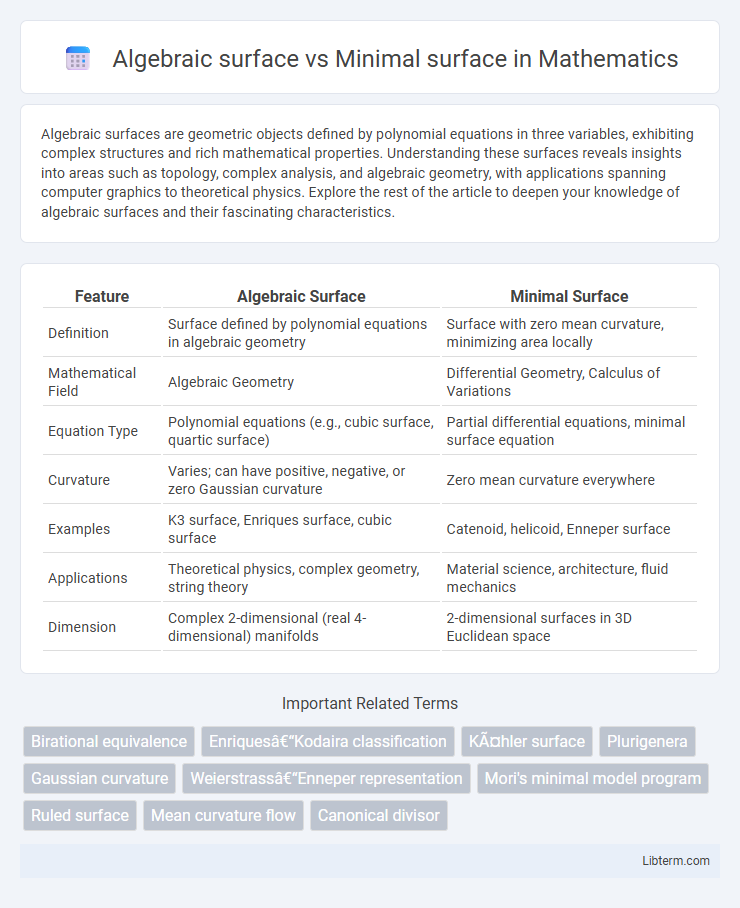
| Feature | Algebraic Surface | Minimal Surface |
|---|---|---|
| Definition | Surface defined by polynomial equations in algebraic geometry | Surface with zero mean curvature, minimizing area locally |
| Mathematical Field | Algebraic Geometry | Differential Geometry, Calculus of Variations |
| Equation Type | Polynomial equations (e.g., cubic surface, quartic surface) | Partial differential equations, minimal surface equation |
| Curvature | Varies; can have positive, negative, or zero Gaussian curvature | Zero mean curvature everywhere |
| Examples | K3 surface, Enriques surface, cubic surface | Catenoid, helicoid, Enneper surface |
| Applications | Theoretical physics, complex geometry, string theory | Material science, architecture, fluid mechanics |
| Dimension | Complex 2-dimensional (real 4-dimensional) manifolds | 2-dimensional surfaces in 3D Euclidean space |
Introduction to Algebraic Surfaces
Algebraic surfaces are two-dimensional varieties defined by polynomial equations in three-dimensional projective space, characterized by their algebraic properties such as degree, singularities, and classification within the Enriques-Kodaira framework. Minimal surfaces, a subset within algebraic surfaces, are those that cannot be simplified further via birational transformations without increasing their complexity, representing the simplest models in their birational equivalence class. Introduction to algebraic surfaces involves studying their geometric structures, divisor class groups, and the interplay between algebraic and differential properties to understand their classification and moduli.
Defining Minimal Surfaces
Minimal surfaces are defined as surfaces with zero mean curvature at every point, representing critical points of the area functional and often modeled by solutions to the minimal surface equation. Algebraic surfaces, in contrast, are defined by polynomial equations in three variables and do not necessarily have zero mean curvature. The study of minimal surfaces intersects with differential geometry and variational calculus, while algebraic surfaces arise primarily in algebraic geometry.
Key Mathematical Foundations
Algebraic surfaces are defined by polynomial equations in three variables, relying on algebraic geometry principles such as sheaf theory and projective varieties, while minimal surfaces are characterized by zero mean curvature and arise in differential geometry through solutions to variational problems minimizing area. The key mathematical foundation for algebraic surfaces includes concepts like divisors, intersection theory, and singularity resolution, whereas minimal surfaces are grounded in partial differential equations, specifically the minimal surface equation and geometric measure theory. Understanding the contrast between complex structure control in algebraic surfaces and curvature minimization in minimal surfaces highlights their distinct roles in modern geometry.
Historical Development and Contributions
Algebraic surfaces, studied extensively since the 19th century through the work of mathematicians like Bernhard Riemann and Max Noether, involve solutions to polynomial equations in three variables, contributing significantly to algebraic geometry's foundation. Minimal surfaces, characterized by zero mean curvature and explored by Joseph Plateau and later refined by Jesse Douglas and Tibor Rado in the early 20th century, advanced the calculus of variations and geometric analysis. The intersection of these two fields has driven progress in understanding complex geometry and topology, influencing modern research in differential geometry and mathematical physics.
Classification and Examples of Algebraic Surfaces
Algebraic surfaces are classified by their Kodaira dimension into categories such as rational, K3, Enriques, and general type surfaces, each defined by the complexity of their canonical bundles. Examples include the projective plane (a rational surface), quartic surfaces in \(\mathbb{P}^3\) representing K3 surfaces, and surfaces of general type like hypersurfaces of high degree. Minimal surfaces, important in differential geometry, are characterized by zero mean curvature and often arise as critical points of area functional, contrasting with algebraic surfaces that are classified via birational geometry and complex structure.
Properties and Equations of Minimal Surfaces
Minimal surfaces are defined as surfaces exhibiting zero mean curvature at every point, characterized by solutions to the minimal surface equation, a nonlinear partial differential equation derived from the calculus of variations. Unlike algebraic surfaces, which are described by polynomial equations in three variables, minimal surfaces often require parametric or implicit representations involving elliptic functions or harmonic maps. Key properties of minimal surfaces include stability, local area minimization, and saddle-shaped geometry, with classical examples such as the catenoid and helicoid illustrating the interplay between differential geometry and partial differential equations.
Geometric Interpretations and Visualizations
Algebraic surfaces are defined as zero sets of polynomial equations in three variables, allowing visualization through their intricate geometric structures and singularities that reveal complex topologies. Minimal surfaces, characterized by zero mean curvature, represent surfaces that locally minimize area and exhibit smooth, saddle-shaped geometries often visualized via soap film analogies. Geometric interpretation of algebraic surfaces emphasizes algebraic complexity and singular points, while minimal surfaces focus on curvature properties and stable forms derived from variational principles.
Major Differences: Algebraic vs Minimal Surfaces
Algebraic surfaces are defined by polynomial equations in projective space, characterized by their degree and singularities, while minimal surfaces arise as critical points of the area functional with zero mean curvature. Algebraic surfaces can be compact and complex, often studied in algebraic geometry, whereas minimal surfaces are typically smooth real surfaces studied in differential geometry and can be non-compact. The fundamental difference lies in their definitions: algebraic surfaces are algebraic sets, and minimal surfaces are geometric objects minimizing surface area locally.
Applications in Science and Engineering
Algebraic surfaces defined by polynomial equations find applications in computer graphics and robotics for modeling complex shapes and optimizing motion paths. Minimal surfaces, characterized by zero mean curvature, are crucial in material science and architecture for designing structures with minimal material use and optimal strength, such as soap film-inspired tensile membranes. Both surfaces contribute to advances in fluid dynamics, where algebraic surfaces model boundary conditions and minimal surfaces describe natural interfaces minimizing energy.
Open Problems and Future Research Directions
Algebraic surfaces, defined by polynomial equations, exhibit rich classification challenges linked to their birational geometry, while minimal surfaces, characterized by zero mean curvature, prompt ongoing inquiries into uniqueness and stability conditions in higher dimensions. Open problems include understanding the moduli spaces of algebraic surfaces with specific invariants and uncovering new examples of minimal surfaces with complex topology or boundary conditions. Future research aims to bridge techniques from complex differential geometry and algebraic geometry to resolve conjectures on existence, compactification, and deformation of these surfaces.
Algebraic surface Infographic
 libterm.com
libterm.com