The boxcar function, also known as the rectangular function, is a fundamental mathematical tool used in signal processing and analysis to model idealized pulses or windowing operations. It takes the value of one within a specific interval and zero elsewhere, making it essential for defining time-limited signals and filtering applications. Discover how the boxcar function can enhance your understanding of signal manipulation in the rest of this article.
Table of Comparison
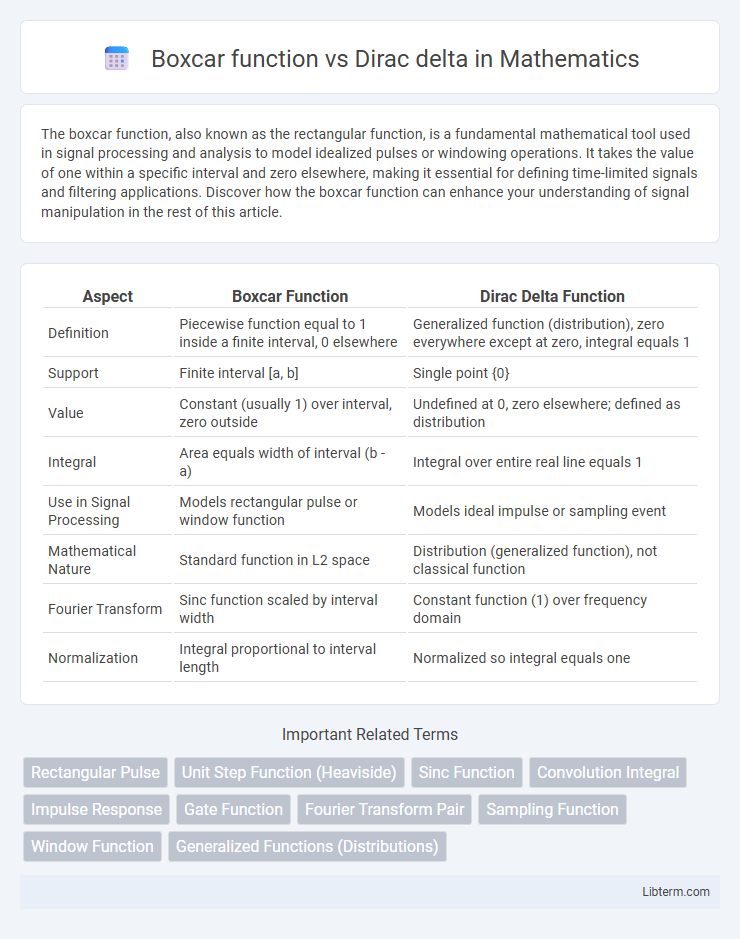
| Aspect | Boxcar Function | Dirac Delta Function |
|---|---|---|
| Definition | Piecewise function equal to 1 inside a finite interval, 0 elsewhere | Generalized function (distribution), zero everywhere except at zero, integral equals 1 |
| Support | Finite interval [a, b] | Single point {0} |
| Value | Constant (usually 1) over interval, zero outside | Undefined at 0, zero elsewhere; defined as distribution |
| Integral | Area equals width of interval (b - a) | Integral over entire real line equals 1 |
| Use in Signal Processing | Models rectangular pulse or window function | Models ideal impulse or sampling event |
| Mathematical Nature | Standard function in L2 space | Distribution (generalized function), not classical function |
| Fourier Transform | Sinc function scaled by interval width | Constant function (1) over frequency domain |
| Normalization | Integral proportional to interval length | Normalized so integral equals one |
Introduction to Boxcar Function and Dirac Delta
The Boxcar function, also known as the rectangular function, is a piecewise function that equals one over a specified interval and zero elsewhere, frequently used to model idealized signals in time and frequency domains. The Dirac delta, or impulse function, serves as a distribution rather than a traditional function, characterized by an infinite peak at zero with an integral of one, enabling idealized sampling and signal analysis in systems and transforms. Both functions play fundamental roles in signal processing and mathematical physics, with the Boxcar function representing finite duration signals and the Dirac delta representing instantaneous impulses.
Mathematical Definitions and Notations
The Boxcar function, often denoted as \(\text{rect}(t)\), is defined as \(\text{rect}(t) = 1\) for \(|t| \leq \frac{1}{2}\) and 0 otherwise, representing a rectangular pulse of unit width centered at zero. The Dirac delta function, \(\delta(t)\), is a distribution defined by the property \(\int_{-\infty}^{\infty} \delta(t) f(t) dt = f(0)\) for any test function \(f(t)\), with \(\delta(t) = 0\) for \(t \neq 0\) and an undefined value at \(t=0\) but an integral of one over the entire real line. While the Boxcar function has finite amplitude and support, the Dirac delta function is idealized as an infinitely high, infinitely narrow spike with unit integral, utilized in signal processing and systems theory to model impulsive input signals.
Visual Representations: Boxcar vs Dirac Delta
The Boxcar function is visually represented as a rectangular pulse with a finite width and constant amplitude, clearly illustrating its defined interval and magnitude. In contrast, the Dirac delta is depicted as an infinitely narrow spike with infinite amplitude at a single point, emphasizing its nature as a distribution rather than a conventional function. These distinct visual characteristics highlight the Boxcar's role in modeling finite duration signals and the Dirac delta's function as an idealized impulse in signal processing and systems analysis.
Key Differences in Properties
The Boxcar function is a rectangular pulse with finite amplitude and duration, defined by a constant value over a specific interval, while the Dirac delta is a distribution characterized by zero width, infinite amplitude, and unit integral. Unlike the Boxcar function, the Dirac delta acts as an identity element in convolution, extracting the value of a function at a single point. The Boxcar function has a finite area equal to amplitude times width, whereas the Dirac delta's integral is always one, representing an idealized impulse.
Applications in Signal Processing
The Boxcar function is frequently used in signal processing for windowing and smoothing operations, particularly in moving average filters, due to its finite and uniform support. The Dirac delta function, characterized by its impulsive nature and infinite peak, serves as an idealized sampling function and is essential for system analysis in the time and frequency domains. Both functions are critical in convolution operations, with the Boxcar function enabling practical signal averaging and the Dirac delta function simplifying system responses and impulse analysis.
Approximating Dirac Delta with Boxcar Function
The Boxcar function serves as a practical approximation of the Dirac delta by narrowing its width while maintaining area unity, effectively mimicking the delta's impulse properties. As the Boxcar function's width approaches zero, its shape converges to the idealized spike of the Dirac delta, making it useful in numerical simulations and signal processing where perfect impulses cannot be realized. This approximation allows for handling distributions in a discrete or finite domain while preserving essential integral properties of the Dirac delta function.
Fourier Transform Comparisons
The Boxcar function, or rectangular function, has a Fourier Transform characterized by a sinc function, indicating finite bandwidth and main lobe with side lobes that decay as frequency increases. In contrast, the Dirac delta function's Fourier Transform is a constant function across all frequencies, representing infinite bandwidth and an equal presence of all frequency components. This fundamental difference highlights the Boxcar function's frequency-limited nature versus the Dirac delta's idealized, uniform spectral distribution.
Role in Convolution Operations
The Boxcar function acts as a finite rectangular window in convolution operations, smoothing or averaging signals over a specific interval by integrating values within its width. The Dirac delta function serves as an identity element in convolution, effectively sampling or extracting the value of a function at a particular point without altering its shape. While the Boxcar function introduces blurring effects due to its finite support, the Dirac delta preserves original signal characteristics by producing exact replicas through convolution.
Practical Examples and Use Cases
The boxcar function, characterized by its finite width and constant amplitude, is commonly used in signal processing for windowing applications such as smoothing and temporal averaging in data analysis. The Dirac delta function, idealized as an impulse with zero width but unit area, is essential in system modeling and control theory for representing instantaneous events and impulse responses. Practical examples include using the boxcar function to model moving average filters in time series data, while the Dirac delta function is fundamental in differential equations and convolution operations in electrical engineering and physics.
Summary: Choosing Between Boxcar and Dirac Delta
The Boxcar function provides a finite-width, rectangular pulse useful for modeling time-limited signals, while the Dirac delta represents an idealized, infinitely narrow impulse with unit area. Choosing between the Boxcar and Dirac delta depends on whether signal duration or instantaneous energy concentration is more critical for the analysis. In practical applications, the Boxcar function suits systems with measurable pulse widths, whereas the Dirac delta is optimal for theoretical models and impulse response characterizations.
Boxcar function Infographic
 libterm.com
libterm.com