Free services and products provide significant value by allowing users to access essential resources without cost, enhancing accessibility and fostering innovation. Many companies leverage free offerings to build customer trust and encourage future purchases. Explore the rest of this article to discover how free options can benefit you and where to find the best opportunities.
Table of Comparison
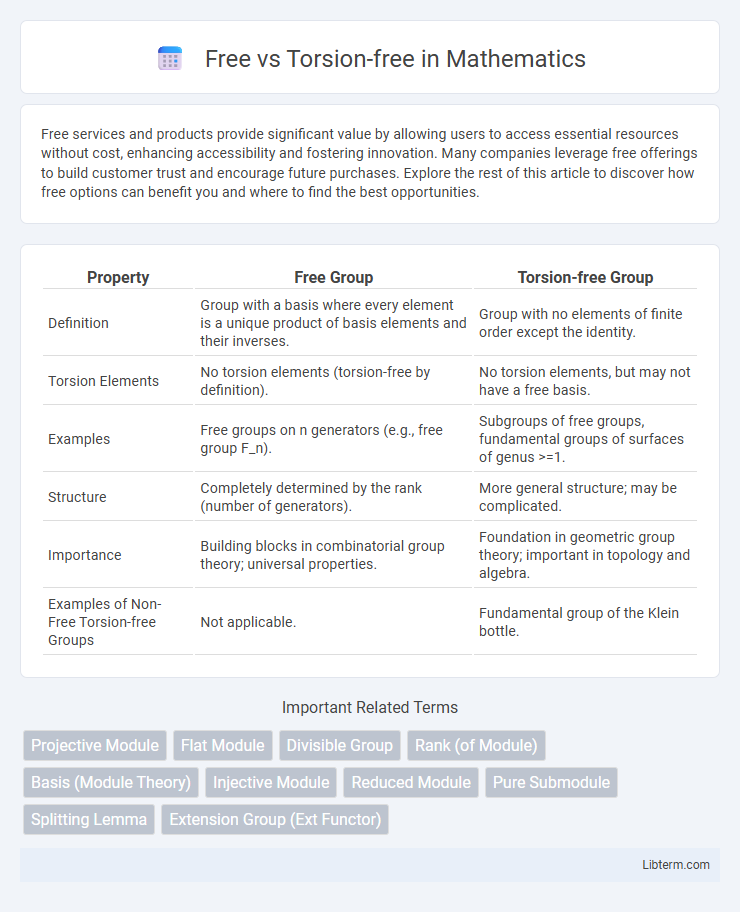
| Property | Free Group | Torsion-free Group |
|---|---|---|
| Definition | Group with a basis where every element is a unique product of basis elements and their inverses. | Group with no elements of finite order except the identity. |
| Torsion Elements | No torsion elements (torsion-free by definition). | No torsion elements, but may not have a free basis. |
| Examples | Free groups on n generators (e.g., free group F_n). | Subgroups of free groups, fundamental groups of surfaces of genus >=1. |
| Structure | Completely determined by the rank (number of generators). | More general structure; may be complicated. |
| Importance | Building blocks in combinatorial group theory; universal properties. | Foundation in geometric group theory; important in topology and algebra. |
| Examples of Non-Free Torsion-free Groups | Not applicable. | Fundamental group of the Klein bottle. |
Introduction to "Free" and "Torsion-Free" Concepts
A free module over a ring R is characterized by the existence of a basis, allowing every element to be uniquely expressed as a linear combination of basis elements with coefficients in R. Torsion-free modules are defined by the absence of nonzero elements annihilated by nonzero ring elements, ensuring no element has finite order except zero. These concepts are foundational in module theory, influencing the study of module structure and classification in algebra.
Defining Free Modules and Groups
Free modules and groups are algebraic structures characterized by the existence of a basis, allowing every element to be uniquely expressed as a linear combination of basis elements with coefficients from the underlying ring or group. Free modules have a basis over a ring and are torsion-free, meaning no nonzero element is annihilated by a nonzero scalar; however, torsion-free modules do not necessarily possess a basis and thus may lack the free structure. The distinction is crucial in module theory and group theory for understanding structural properties, where free modules provide a canonical form, while torsion-free modules guarantee the absence of elements of finite order.
Understanding Torsion-Free Structures
Torsion-free modules are algebraic structures where no element other than zero is annihilated by a nonzero scalar, distinguishing them from free modules which have a basis allowing every element to be uniquely expressed as a finite linear combination of basis elements. Understanding torsion-free structures is essential in module theory because they generalize free modules by relaxing the requirement of a basis while still avoiding torsion elements that complicate algebraic properties. This concept plays a significant role in commutative algebra and algebraic geometry, particularly in the study of integral domains and vector bundles over schemes.
Key Differences Between Free and Torsion-Free
Free modules over a ring allow a basis such that every element can be uniquely expressed as a finite linear combination of basis elements with ring coefficients, ensuring a strong structural framework. Torsion-free modules lack elements annihilated by nonzero ring elements, meaning no nonzero element is 'killed' by multiplication with a nonzero scalar, but they may not possess a basis. The key difference lies in that all free modules are torsion-free due to their basis, but not all torsion-free modules are free, especially over rings that are not principal ideal domains (PIDs).
Examples of Free vs Torsion-Free Modules
Free modules over a ring R, such as R^n, have a basis allowing every element to be uniquely expressed as a finite linear combination of basis elements, like the module Z^2 over the integers. Torsion-free modules, like the submodule 2Z of Z, contain no elements annihilated by nonzero scalars but may lack a basis, making them not necessarily free; for example, Z as a module over the ring Z is torsion-free but not free when considered over itself with some additional structure. The distinction is critical in module theory, where free modules generalize vector spaces, and torsion-free modules extend the concept of elements with infinite order.
Algebraic Properties and Implications
Free modules possess a basis allowing every element to be uniquely expressed as a linear combination of basis elements, ensuring no torsion elements exist, which means they are inherently torsion-free. Torsion-free modules generalize this concept by having no nonzero element annihilated by a nonzero scalar, but they may lack a basis and fail to be free, especially over rings that are not principal ideal domains. The distinction impacts homological properties and classification, as free modules are projective and fully decomposable, while torsion-free modules can exhibit more complex structures reflecting the underlying ring's algebraic properties.
Applications in Algebra and Topology
Free modules and torsion-free modules play distinct roles in algebra and topology, with free modules serving as fundamental building blocks characterized by a basis that allows direct decomposition, crucial for linear algebra and homological algebra computations. Torsion-free modules, lacking elements annihilated by nonzero scalars, are essential in number theory and algebraic geometry for analyzing integral domains and sheaf cohomology, ensuring stability under extensions. In topology, free modules model homology groups of spaces with trivial torsion, while torsion-free modules provide insight into spaces with more complex structures, such as covering space theory and classification of fiber bundles.
Criteria for Determining Freeness and Torsion-Freeness
Freeness in modules is characterized by the existence of a basis that allows every element to be uniquely expressed as a finite linear combination of basis elements, ensuring a direct sum decomposition into copies of the ring. Torsion-freeness is determined by the absence of nonzero elements annihilated by nonzero ring elements, ensuring no torsion elements disrupt module structure. The key criterion distinguishing free from torsion-free modules is the presence of a basis for free modules, whereas torsion-free modules may lack such a basis but still prohibit torsion elements.
Common Misconceptions and Challenges
Many learners mistakenly assume all torsion-free modules are free, overlooking that torsion-free only guarantees no elements of finite order, while freeness requires a basis spanning the entire module. This misconception leads to challenges in distinguishing when a module is genuinely free, especially over integral domains where torsion-free modules do not always admit a basis. Recognizing the subtleties between these concepts is critical for understanding module theory and avoiding oversimplifications in algebraic structures.
Conclusion and Summary of Main Points
Free groups are characterized by having a basis such that every element can be uniquely represented as a finite product of basis elements and their inverses, ensuring no relations other than those required by group axioms. Torsion-free groups lack nontrivial elements of finite order, meaning no element other than the identity satisfies a finite power equal to the identity. While every free group is torsion-free, the converse is not true; torsion-free groups can have more complex structures without a free basis, highlighting the distinction in algebraic properties and applications.
Free Infographic
 libterm.com
libterm.com