The greatest lower bound, or infimum, represents the highest value that is less than or equal to every element in a given set, providing a critical measure in order theory and analysis. It is instrumental in understanding bounds within sequences, functions, and subsets of real numbers, ensuring that no element falls below this threshold. Explore the rest of this article to deepen Your understanding of how the greatest lower bound applies in various mathematical contexts.
Table of Comparison
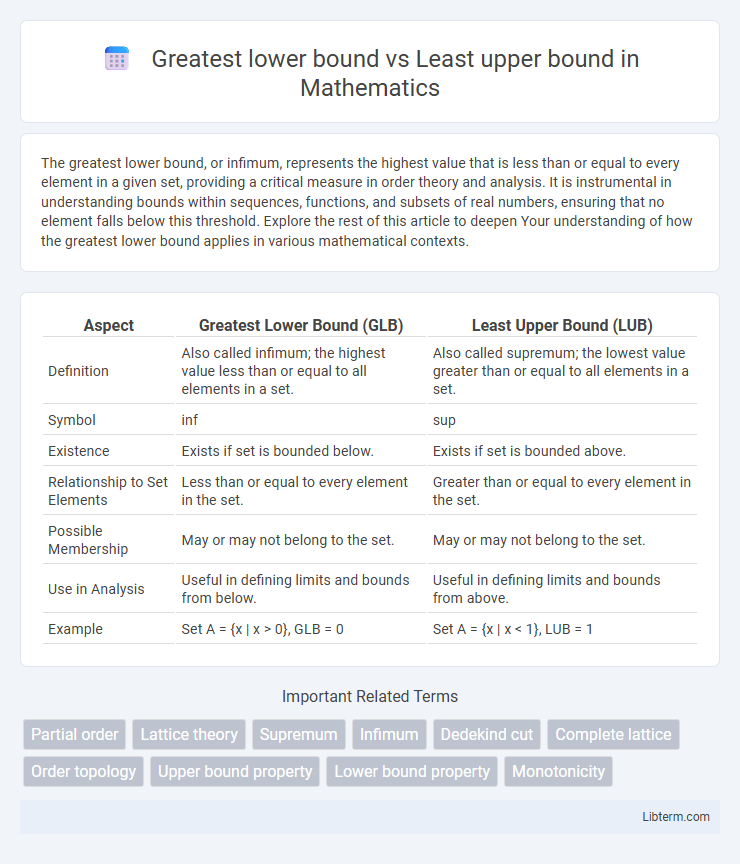
| Aspect | Greatest Lower Bound (GLB) | Least Upper Bound (LUB) |
|---|---|---|
| Definition | Also called infimum; the highest value less than or equal to all elements in a set. | Also called supremum; the lowest value greater than or equal to all elements in a set. |
| Symbol | inf | sup |
| Existence | Exists if set is bounded below. | Exists if set is bounded above. |
| Relationship to Set Elements | Less than or equal to every element in the set. | Greater than or equal to every element in the set. |
| Possible Membership | May or may not belong to the set. | May or may not belong to the set. |
| Use in Analysis | Useful in defining limits and bounds from below. | Useful in defining limits and bounds from above. |
| Example | Set A = {x | x > 0}, GLB = 0 | Set A = {x | x < 1}, LUB = 1 |
Understanding Bounds: An Introduction
Greatest lower bound (GLB) and least upper bound (LUB) represent fundamental concepts in order theory, defining the highest element that is less than or equal to all elements in a subset and the lowest element that is greater than or equal to all elements in a subset, respectively. These bounds underpin completeness properties in partially ordered sets, with GLB also known as infimum and LUB as supremum. Understanding how GLB and LUB interact aids in grasping lattice structures and optimizing problems within mathematical analysis and computer science.
Defining Greatest Lower Bound (Infimum)
The greatest lower bound (infimum) of a set is the largest value that is less than or equal to every element in the set, ensuring no smaller number has the same property. It provides a precise lower boundary even when the minimum does not exist within the set, critical in real analysis and order theory. The infimum is unique when it exists and serves as a foundational concept in lattice theory, optimization, and function limits.
Exploring Least Upper Bound (Supremum)
The least upper bound, or supremum, of a set is the smallest value that is greater than or equal to every element in that set, playing a crucial role in real analysis and order theory. Unlike the greatest lower bound (infimum), which identifies the largest element less than or equal to all in the set, the supremum may not be an element of the set itself but guarantees the tightest upper limit. This concept is essential for defining limits, integrating bounded functions, and understanding the completeness property of the real numbers.
Key Differences: Greatest Lower Bound vs Least Upper Bound
The greatest lower bound (GLB) of a set is the highest element that is less than or equal to all elements in the set, while the least upper bound (LUB) is the lowest element that is greater than or equal to all elements in the set. GLB is also known as the infimum, and LUB as the supremum, both essential concepts in order theory and real analysis. Key differences include their positions relative to the set: GLB lies below or equal to all elements, whereas LUB lies above or equal to all elements, highlighting their complementary roles in bounding sets.
Mathematical Notation and Terminology
The greatest lower bound (glb), denoted as infimum (inf), represents the largest element that is less than or equal to all elements in a subset of a partially ordered set, commonly expressed as inf(S). The least upper bound (lub), known as supremum (sup), is the smallest element greater than or equal to every element in the subset, denoted sup(S). Both concepts rely on order relations and are fundamental in lattice theory and real analysis for defining bounds within sets.
Visualizing Bounds with Examples
Greatest lower bound (GLB) and least upper bound (LUB) represent key concepts in order theory, visualized conceptually as the highest point below all elements and the lowest point above all elements in a set, respectively. For example, considering the set {2, 3, 5} on the number line, the GLB of {3, 5, 7} is 3, while the LUB of {1, 2, 3} is 3. Plotting these sets helps illustrate that the GLB anchors from below, ensuring no greater lower point exists, whereas the LUB caps from above, guaranteeing no smaller upper point exists within the ordered structure.
Importance of Bounds in Real Analysis
Greatest lower bound (infimum) and least upper bound (supremum) are fundamental concepts in real analysis critical for understanding the completeness property of the real numbers. These bounds enable precise descriptions of limits, convergence, and continuity by providing exact thresholds within which sequences or sets are contained. The existence of supremum and infimum for every bounded set underpins many theorems, such as the Monotone Convergence Theorem and the Bolzano-Weierstrass Theorem, making them indispensable tools for rigorous mathematical analysis.
Applications in Calculus and Optimization
Greatest lower bound (infimum) and least upper bound (supremum) play crucial roles in calculus by defining precise boundaries for sequences and function limits, ensuring convergence criteria are rigorously met. In optimization, these bounds are essential for identifying optimal solutions within feasible regions, particularly in convex analysis and constrained optimization problems. Their use facilitates the establishment of minimum and maximum values in both continuous and discrete domains, enhancing algorithmic efficiency and solution accuracy.
Common Mistakes and Misconceptions
Greatest lower bound (GLB) and least upper bound (LUB) are often confused, leading to the mistaken belief that they must be actual elements of the set, when they can instead be limits not contained within the set. Another common misconception is assuming the GLB is always smaller than or equal to every element while ignoring it may not be the minimum, and similarly, the LUB may not be the maximum but only an upper bound. Misinterpretation arises from mixing up GLB with minimum and LUB with maximum, overlooking that these bounds describe constraints rather than guaranteed members of the set.
Frequently Asked Questions on Bounds
The greatest lower bound (infimum) of a set is the largest value that is less than or equal to every element in the set, while the least upper bound (supremum) is the smallest value greater than or equal to every element. Frequently asked questions about bounds often address how to determine if a set has a supremum or infimum and the difference between these bounds and minimum or maximum values. In real analysis, the completeness property ensures that every non-empty set bounded above has a least upper bound, and every non-empty set bounded below has a greatest lower bound.
Greatest lower bound Infographic
 libterm.com
libterm.com