Enhance your daily routine with this innovative product designed to simplify tasks and improve efficiency. Engineered with cutting-edge technology, it offers unmatched performance and reliability to meet your needs. Discover how this solution transforms your experience by reading the full article.
Table of Comparison
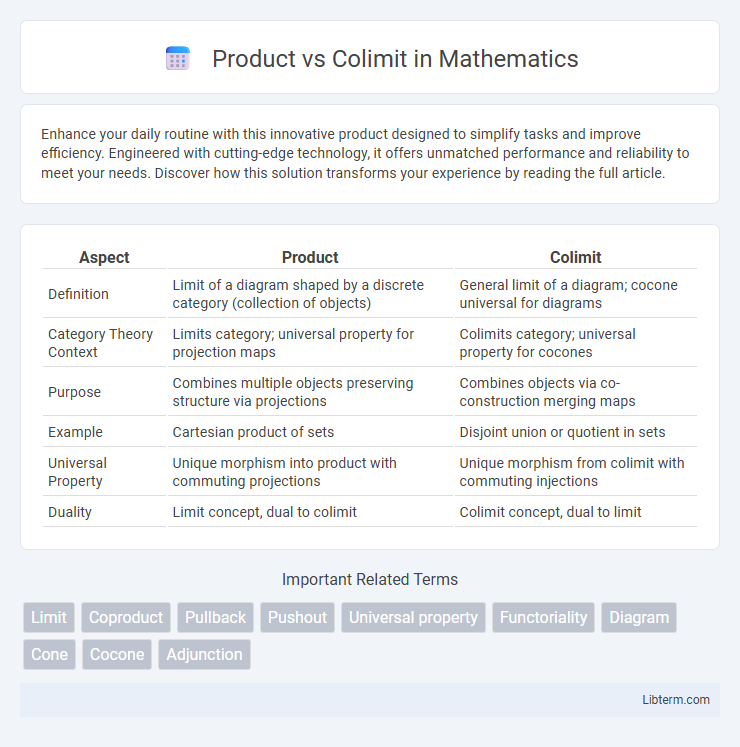
| Aspect | Product | Colimit |
|---|---|---|
| Definition | Limit of a diagram shaped by a discrete category (collection of objects) | General limit of a diagram; cocone universal for diagrams |
| Category Theory Context | Limits category; universal property for projection maps | Colimits category; universal property for cocones |
| Purpose | Combines multiple objects preserving structure via projections | Combines objects via co-construction merging maps |
| Example | Cartesian product of sets | Disjoint union or quotient in sets |
| Universal Property | Unique morphism into product with commuting projections | Unique morphism from colimit with commuting injections |
| Duality | Limit concept, dual to colimit | Colimit concept, dual to limit |
Introduction to Products and Colimits
Products and colimits are fundamental constructions in category theory that generalize notions of limits and unions. A product represents the categorical form of a Cartesian product, serving as a universal object equipped with projection morphisms to individual components. Colimits, on the other hand, unify diagrams by providing a universal cocone, encompassing coproducts, coequalizers, and colimits of more complex shapes.
Fundamental Concepts: Products in Category Theory
Products in category theory represent a universal construction capturing the notion of pairing objects alongside projection morphisms that retrieve components. A product of objects \(A\) and \(B\) in a category is an object \(P\) equipped with morphisms \(p_A: P \to A\) and \(p_B: P \to B\) such that for any object \(X\) with morphisms \(f: X \to A\) and \(g: X \to B\), there exists a unique morphism \(u: X \to P\) making the diagrams commute. This universal property characterizes products as limits over discrete diagrams, serving as fundamental constructs to systematically encode joint information in categorical contexts.
Understanding Colimits: Definitions and Intuition
Colimits generalize the notion of merging objects along a diagram in category theory, representing the most efficient way to coalesce a system of morphisms into a single universal object. Unlike products that capture the universal construction of objects with projection maps, colimits focus on cocones and the universal property that mediates morphisms from the diagram to the colimit. Understanding colimits involves grasping their role in identifying the "least common extension" of objects and morphisms, which can instantiate coproducts, pushouts, or directed colimits depending on the diagram's shape.
Key Differences Between Products and Colimits
Products represent limits in category theory characterized by universal cones from a given family of objects, forming a unique object with projection morphisms that factor through any other cone. Colimits, in contrast, describe universal cocones to a diagram, often manifesting as coproducts or coequalizers, and provide an object amalgamating the diagram's objects through injection morphisms. Key differences include the direction of morphisms--products use projections (limits) while colimits use injections (colimits)--and their universal property roles, with products consolidating information via limiting cones and colimits integrating structures through cocones.
Universal Properties: Comparing Product and Colimit
Product and colimit both satisfy universal properties, defining unique morphisms that factor through them. The product's universal property requires a cone from an object to each component, ensuring a unique morphism into the product. The colimit's universal property, dual to the product, involves a cocone from components to an object, guaranteeing a unique morphism from the colimit.
Examples of Products in Various Categories
Products in category theory represent the categorical analog of Cartesian products, appearing as objects paired with projection morphisms that universally factor through any other object connecting to the same components. In the category of sets, the product is exemplified by the Cartesian product alongside projection functions onto each set, and in the category of topological spaces, the product involves the Cartesian product of underlying sets with the product topology ensuring continuity of projections. Further examples include the direct product of groups capturing group elements paired coordinate-wise, and the product in the category of vector spaces represented by the direct sum equipped with coordinate projection linear maps.
Exploring Colimit Types: Coproducts, Pushouts, and More
Colimits in category theory generalize constructions like coproducts, pushouts, and coequalizers, capturing how objects combine or are identified in universal ways. Coproducts represent categorical sums, combining objects disjointly, while pushouts model the amalgamation of objects over a common subobject, enabling the merging of shared structures. Understanding these colimit types reveals their roles in constructing complex objects from simpler components, contrasting with products that represent categorical products or intersections in a universal manner.
Applications of Products in Mathematics and Computer Science
Products in mathematics and computer science serve as fundamental constructs for combining objects or data structures, enabling the representation of pairs, tuples, or Cartesian products in set theory and algebra. In category theory, products provide a way to model parallel computations, data aggregation, and multi-parameter functions, facilitating operations in programming languages and database theory. Applications include defining product types in functional programming, constructing state spaces in automata theory, and formulating multi-input systems in systems theory, highlighting their versatility in structuring complex mathematical and computational systems.
Practical Uses of Colimits in Theory and Practice
Colimits serve as a fundamental tool in category theory for constructing objects by coherently combining multiple components, contrasting with products that represent structured tuples of objects. Practical uses of colimits include modeling complex systems in algebraic topology, where pushouts describe glued spaces, and in computer science for merging data types or schemas. These constructions enable flexible aggregation and transformation of information, making colimits indispensable for theoretical developments and practical applications in modular design and data integration.
Summary: Choosing Between Products and Colimits
Products capture the universal property of objects paired with projection maps, suitable for constructing tuples or simultaneous objects, while colimits represent the universal property of cocones, ideal for amalgamating diagrams or merging objects. Selecting between products and colimits depends on whether the goal is to unify multiple objects into a single structured entity through projections or to combine objects via cocones reflecting identifications or limits. In practice, products are prevalent in constructing object tuples or pullbacks, whereas colimits are essential in forming unions, pushouts, and quotients in category theory.
Product Infographic
 libterm.com
libterm.com