A continuous map is a fundamental concept in topology referring to a function between two topological spaces where the preimage of every open set is open, ensuring no abrupt changes in the mapping. This property is essential for studying the behavior of spaces and their transformations, providing a rigorous way to understand continuity beyond simple real-valued functions. Explore the rest of the article to deepen your understanding of continuous maps and their applications in various mathematical contexts.
Table of Comparison
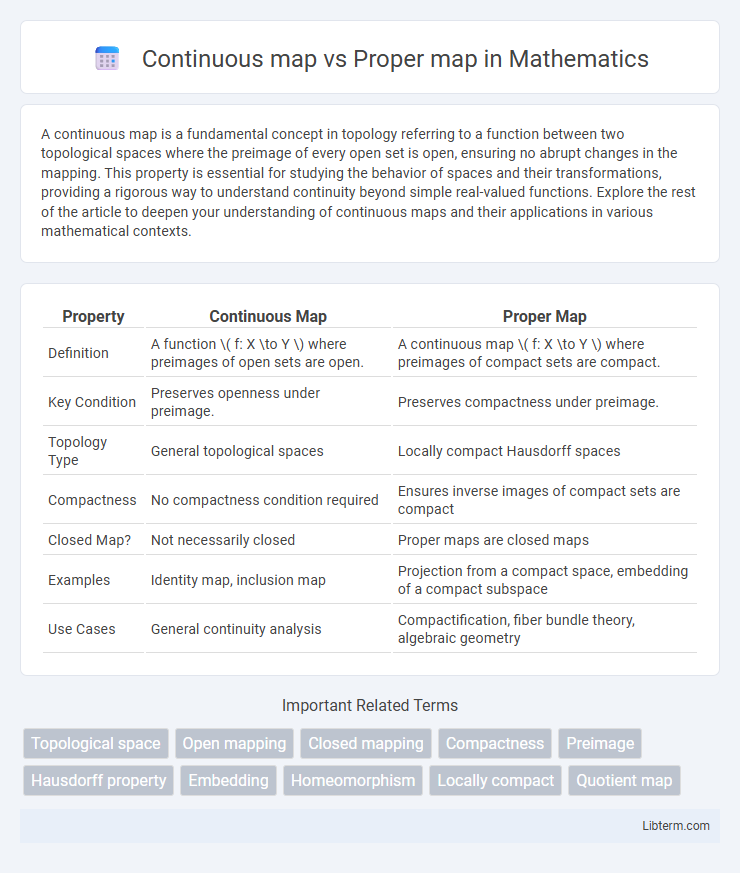
| Property | Continuous Map | Proper Map |
|---|---|---|
| Definition | A function \( f: X \to Y \) where preimages of open sets are open. | A continuous map \( f: X \to Y \) where preimages of compact sets are compact. |
| Key Condition | Preserves openness under preimage. | Preserves compactness under preimage. |
| Topology Type | General topological spaces | Locally compact Hausdorff spaces |
| Compactness | No compactness condition required | Ensures inverse images of compact sets are compact |
| Closed Map? | Not necessarily closed | Proper maps are closed maps |
| Examples | Identity map, inclusion map | Projection from a compact space, embedding of a compact subspace |
| Use Cases | General continuity analysis | Compactification, fiber bundle theory, algebraic geometry |
Introduction to Continuous and Proper Maps
Continuous maps between topological spaces preserve the structure by ensuring the preimage of every open set is open, forming the foundation of topology and analysis. Proper maps are a special class of continuous maps characterized by the preimage of every compact set being compact, which is crucial in studying compactness properties and ensuring nice behavior in topological and geometric contexts. Understanding the distinctions and applications of continuous and proper maps is essential for advanced topics in topology, differential geometry, and algebraic geometry.
Defining Continuous Maps
Continuous maps between topological spaces are functions where the preimage of every open set is open, ensuring the preservation of topological structure under mapping. Proper maps are a subset of continuous maps characterized by the preimage of every compact set being compact, which guarantees stronger compactness properties and better control over the behavior at infinity. Understanding continuous maps is essential to grasp the more restrictive notion of proper maps and their applications in topology and geometry.
Understanding Proper Maps
A proper map is a continuous function between topological spaces where the preimage of every compact set is compact, ensuring better control over the behavior at infinity compared to general continuous maps. Understanding proper maps involves recognizing their role in guaranteeing properties such as closedness and compactness preservation, which are crucial in algebraic topology and manifold theory. Properness strengthens continuity by linking topological compactness with the mapping structure, making these maps essential in applications like fiber bundle theory and the study of non-compact manifolds.
Key Differences Between Continuous and Proper Maps
Continuous maps ensure that the preimage of every open set is open, preserving topological structure without strict constraints on compactness. Proper maps require the preimage of every compact set to be compact, guaranteeing stronger control over the behavior of spaces especially in relation to compactness and boundary properties. This distinction makes proper maps particularly important in areas like algebraic topology and differential geometry where compactness conditions influence continuity and structure preservation.
Properties of Continuous Maps
Continuous maps preserve the structure of topological spaces by ensuring the preimage of every open set is open, supporting fundamental properties like limit preservation and connectedness. These maps guarantee the image of compact sets remains compact when the underlying space is Hausdorff, but this property alone does not imply properness. Proper maps extend continuity by additionally requiring the preimage of every compact set to be compact, strengthening control over the map's behavior in topological and geometric contexts.
Properties of Proper Maps
Proper maps are continuous functions between topological spaces where the preimage of every compact set is compact, ensuring strong control over the behavior at infinity. They are closed maps, preserving compactness and often yielding properness conditions essential in algebraic geometry and differential topology. In contrast, continuous maps may lack these compactness-preserving properties, making proper maps crucial for robust continuity with topological finiteness constraints.
Examples of Continuous Maps
Continuous maps, defined as functions where the preimage of every open set is open, include examples such as polynomials like f(x) = x2 on the real line and trigonometric functions like sin(x). They preserve limits and topological structure without necessarily being proper, as proper maps require the preimage of every compact set to be compact, like the inclusion map from a closed interval [0,1] into the real line. Continuous maps are fundamental in topology and differential geometry, enabling analysis of space structure without the compactness constraints critical for proper maps.
Examples of Proper Maps
Proper maps are continuous functions between topological spaces where the preimage of every compact set is compact; common examples include closed embeddings, such as the inclusion of a closed interval [0,1] into the real line R. Another example is the projection map from a product space like X x Y to X when Y is compact, ensuring that inverse images of compact sets remain compact. In algebraic geometry, proper morphisms generalize these notions, exemplified by projective varieties mapping onto a base space where fibers are compact in the Zariski topology.
Applications in Topology and Mathematics
Continuous maps preserve the topological structure by ensuring the preimage of every open set is open, fundamental in defining homeomorphisms and studying continuous deformations in topology. Proper maps, characterized by the preimage of every compact set being compact, are essential in compactification processes and in the study of manifolds, particularly in extending local properties to global contexts. Applications in algebraic topology, differential geometry, and complex analysis rely heavily on the interplay between continuous and proper maps to analyze space embeddings, fiber bundles, and compactness-related invariants.
Summary: Choosing Between Continuous and Proper Maps
Continuous maps preserve the structure of topological spaces by ensuring the preimage of every open set is open, making them fundamental in analysis and topology. Proper maps strengthen this concept by requiring the preimage of every compact set to be compact, which is crucial for controlling behavior at infinity and ensuring nice compactness properties. Selecting between continuous and proper maps depends on whether preserving local continuity suffices or if handling compactness and boundary behavior in applications like manifold theory or algebraic geometry is necessary.
Continuous map Infographic
 libterm.com
libterm.com