Cohomology groups provide a powerful algebraic tool to classify and measure the topological features of spaces, capturing information about their shape and structure through algebraic invariants. They play a crucial role in various branches of mathematics, including geometry, topology, and algebra, by enabling computations related to holes, connectivity, and obstructions. Explore the rest of the article to deepen your understanding of how cohomology groups reveal the hidden properties of complex spaces.
Table of Comparison
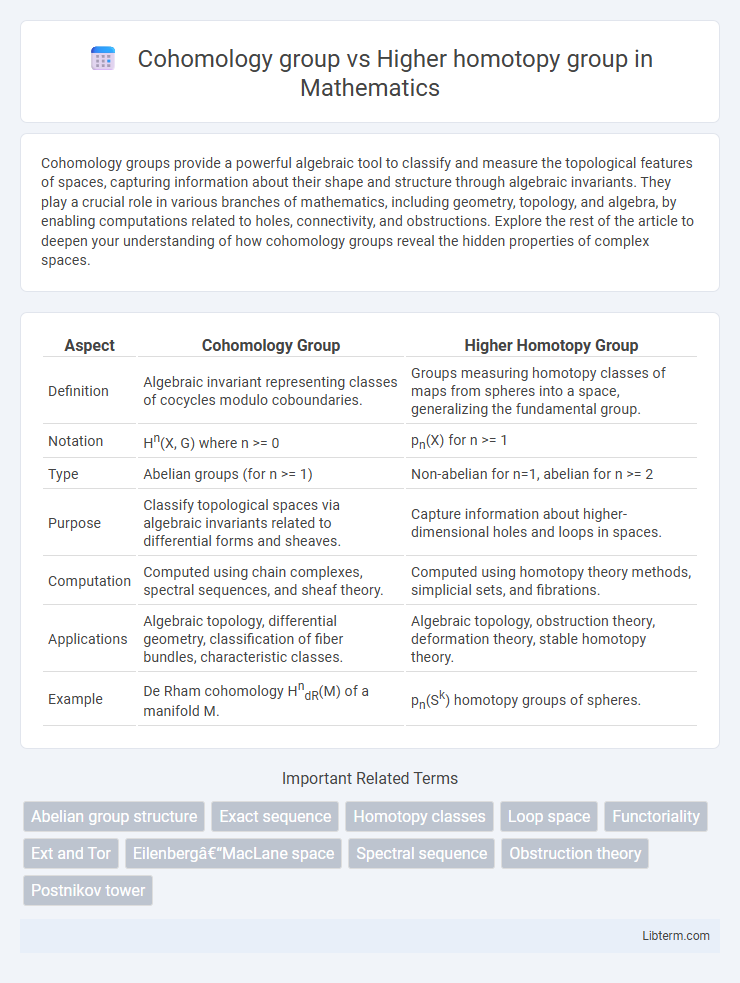
| Aspect | Cohomology Group | Higher Homotopy Group |
|---|---|---|
| Definition | Algebraic invariant representing classes of cocycles modulo coboundaries. | Groups measuring homotopy classes of maps from spheres into a space, generalizing the fundamental group. |
| Notation | Hn(X, G) where n >= 0 | pn(X) for n >= 1 |
| Type | Abelian groups (for n >= 1) | Non-abelian for n=1, abelian for n >= 2 |
| Purpose | Classify topological spaces via algebraic invariants related to differential forms and sheaves. | Capture information about higher-dimensional holes and loops in spaces. |
| Computation | Computed using chain complexes, spectral sequences, and sheaf theory. | Computed using homotopy theory methods, simplicial sets, and fibrations. |
| Applications | Algebraic topology, differential geometry, classification of fiber bundles, characteristic classes. | Algebraic topology, obstruction theory, deformation theory, stable homotopy theory. |
| Example | De Rham cohomology HndR(M) of a manifold M. | pn(Sk) homotopy groups of spheres. |
Introduction to Cohomology and Homotopy Groups
Cohomology groups provide algebraic invariants that classify topological spaces by encoding information about their structure through cochains, cocycles, and coboundaries, often applied in algebraic topology to detect holes of various dimensions. Higher homotopy groups, denoted p_n for n > 1, generalize the fundamental group by capturing the ways n-dimensional spheres map into a space, revealing deeper layers of connectivity beyond loops. Both concepts serve as fundamental tools in topology, with cohomology emphasizing algebraic duality and higher homotopy groups focusing on homotopical properties of spaces.
Mathematical Foundations of Cohomology Groups
Cohomology groups arise from chain complexes and provide algebraic invariants that classify topological spaces via cochain modules and coboundary operators, capturing global properties such as holes and obstructions. Higher homotopy groups generalize the fundamental group by encoding homotopy classes of maps from n-spheres into a space, reflecting the space's higher-dimensional loop structures but are often more difficult to compute than cohomology groups. The mathematical foundations of cohomology groups involve derived functors, sheaf cohomology, and spectral sequences, which enable systematic computation and deep connections to geometry, algebraic topology, and homological algebra.
Understanding Higher Homotopy Groups
Higher homotopy groups, denoted as p_n(X) for n > 1, capture information about n-dimensional holes in a topological space X, generalizing the fundamental group p_1(X). Unlike cohomology groups, which are abelian and arise from algebraic invariants associated with cochains and cocycles, higher homotopy groups reflect the structure of continuous maps from n-spheres into X, providing richer insights into the space's global shape and homotopy type. Understanding higher homotopy groups is crucial for classifying spaces up to homotopy equivalence and plays a fundamental role in advanced algebraic topology and homotopical algebra.
Historical Context and Development
Cohomology groups emerged in the early 20th century as an algebraic tool to classify topological spaces, with foundational work by Henri Poincare and Elie Cartan, providing invariants that capture global properties through algebraic structures like groups and rings. Higher homotopy groups, introduced by Witold Hurewicz in the 1930s, extended the concept of the fundamental group to capture multi-dimensional loop structures in spaces, revealing deeper layers of topological complexity. Both theories evolved through the mid-20th century via contributions from mathematicians such as J.H.C. Whitehead and Jean Leray, intertwining algebraic methods to enhance understanding of manifold structures and paving the way for modern algebraic topology.
Algebraic Structures in Cohomology vs. Homotopy
Cohomology groups possess a graded ring structure endowed with cup products, enabling rich algebraic operations such as Massey products and providing invariants for distinguishing topological spaces. Higher homotopy groups, though often non-abelian and lacking ring structures, capture complex homotopical information through their composition laws and action of fundamental groups. The interplay between these algebraic structures facilitates deep insights in algebraic topology, with cohomology groups offering computable invariants and higher homotopy groups revealing subtler, non-linear topological features.
Computational Techniques for Both Groups
Computational techniques for cohomology groups often involve spectral sequences, chain complexes, and algorithmic approaches using software like SageMath or Macaulay2 to analyze topological spaces' algebraic structures. Higher homotopy groups require more intricate methods such as obstruction theory, Postnikov towers, and the use of homotopy spectral sequences, with computational tools being less developed but advancing through methods in homotopical algebra and infinity-categories. Effective calculation of both groups combines algebraic topology, homological algebra, and computational algebra systems to handle the complexities inherent in these topological invariants.
Relationships and Interactions Between the Groups
Cohomology groups and higher homotopy groups both capture topological invariants but differ in algebraic structure; cohomology groups form graded rings reflecting global properties, while higher homotopy groups are non-abelian in low dimensions and capture homotopy classes of spheres maps. The Hurewicz theorem links the first nontrivial higher homotopy group to homology, allowing partial computation of these complex groups using cohomological methods. Spectral sequences, such as the Serre spectral sequence, facilitate understanding interactions by relating fiber bundle homotopy groups to cohomology groups, revealing deep connections between their algebraic and geometric structures.
Applications in Topology and Geometry
Cohomology groups provide algebraic invariants that classify topological spaces through structures like de Rham cohomology and Cech cohomology, facilitating the study of manifolds, fiber bundles, and characteristic classes in geometry. Higher homotopy groups capture information about n-dimensional holes and fundamental group generalizations, playing a crucial role in obstruction theory, homotopy classification of maps, and the study of fibration sequences. Applications in topology rely on cohomology for computational techniques and invariants, while higher homotopy groups enable insights into space connectivity and homotopy types beyond the fundamental group.
Key Examples Illustrating Differences
Cohomology groups, such as the singular cohomology group H^n(X; Z), classify topological spaces by measuring the obstructions to constructing global sections, with key examples including the de Rham cohomology of smooth manifolds and Cech cohomology in algebraic topology. Higher homotopy groups p_n(X), starting from p_2(X) onward, capture more subtle homotopy classes of maps from spheres into the space X, exemplified by p_2(S^2) Z and the notoriously complex p_3(S^2) Z, which reflects nontrivial "higher-dimensional hole" structures. These groups differ fundamentally as cohomology groups form abelian groups related to dual algebraic invariants, while higher homotopy groups reveal non-abelian and topological structure intrinsic to the space's shape beyond what cohomology detects.
Future Directions and Open Questions
Future directions in the study of cohomology groups and higher homotopy groups involve exploring deeper connections through generalized cohomology theories and higher category theory frameworks. Open questions include understanding the full impact of these structures in stable homotopy theory and their applications in quantum field theory and algebraic geometry. Advancements in computational methods and the development of new invariants are expected to shed light on unresolved classification problems and dualities.
Cohomology group Infographic
 libterm.com
libterm.com