Differential geometry explores curves, surfaces, and manifolds using calculus and linear algebra to understand their properties and structures. This field plays a crucial role in modern physics, computer graphics, and robotics by describing the shape and behavior of objects in space. Discover how differential geometry can deepen your understanding of the world by reading the rest of the article.
Table of Comparison
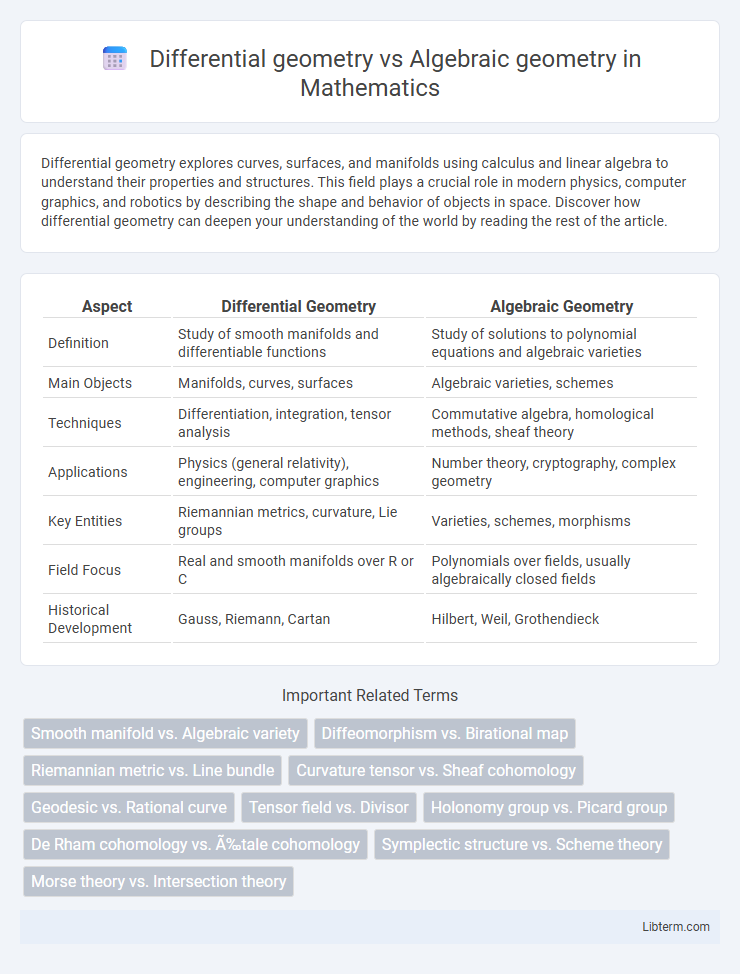
| Aspect | Differential Geometry | Algebraic Geometry |
|---|---|---|
| Definition | Study of smooth manifolds and differentiable functions | Study of solutions to polynomial equations and algebraic varieties |
| Main Objects | Manifolds, curves, surfaces | Algebraic varieties, schemes |
| Techniques | Differentiation, integration, tensor analysis | Commutative algebra, homological methods, sheaf theory |
| Applications | Physics (general relativity), engineering, computer graphics | Number theory, cryptography, complex geometry |
| Key Entities | Riemannian metrics, curvature, Lie groups | Varieties, schemes, morphisms |
| Field Focus | Real and smooth manifolds over R or C | Polynomials over fields, usually algebraically closed fields |
| Historical Development | Gauss, Riemann, Cartan | Hilbert, Weil, Grothendieck |
Overview of Differential Geometry and Algebraic Geometry
Differential geometry studies smooth shapes and curves using calculus and differential equations to analyze properties like curvature and topology on differentiable manifolds. Algebraic geometry focuses on solutions to polynomial equations and the geometric structures they form, using tools from abstract algebra to explore varieties and schemes over different fields. Both fields intersect in areas such as complex manifolds and moduli spaces, bridging continuous and algebraic perspectives on geometry.
Historical Development and Foundations
Differential geometry originated in the 18th century with the study of curves and surfaces using calculus, pioneered by mathematicians such as Gauss and Riemann, focusing on smooth manifolds and curvature. Algebraic geometry developed from solving polynomial equations and studying algebraic varieties, rooted in the work of Descartes and later refined by Hilbert and Grothendieck, emphasizing abstract algebraic structures and schemes. Both fields share a common origin in geometry but diverged through their foundational methodologies: analysis-based techniques for differential geometry and algebraic, scheme-theoretic frameworks for algebraic geometry.
Key Concepts and Structures
Differential geometry studies smooth manifolds using tools like tangent spaces, Riemannian metrics, and curvature to analyze geometric properties through calculus. Algebraic geometry focuses on solutions of polynomial equations, employing schemes, varieties, and sheaves to understand geometric structures defined algebraically. While differential geometry emphasizes smoothness and local behavior, algebraic geometry explores global properties and singularities within an algebraic framework.
Methods and Tools in Differential Geometry
Differential geometry employs methods such as calculus on manifolds, tensor analysis, and connections to study smooth shapes and curves, emphasizing local properties through differentiable maps. Key tools include Riemannian metrics for measuring distances and angles, Lie groups for symmetry analysis, and differential forms used in integration on manifolds. These techniques contrast with algebraic geometry's reliance on polynomial equations and scheme theory to investigate geometric structures from an algebraic perspective.
Methods and Tools in Algebraic Geometry
Algebraic geometry employs tools such as Grothendieck's schemes, cohomology theories, and sheaf theory to study solutions of polynomial equations through geometric structures. It uses commutative algebra, including ideals and varieties, alongside homological algebra techniques to analyze complex varieties and moduli spaces. Contrasting with differential geometry's reliance on smooth manifolds and differential forms, algebraic geometry emphasizes algebraic methods that facilitate understanding of geometric objects defined over arbitrary fields.
Types of Spaces and Manifolds
Differential geometry primarily studies smooth manifolds, such as Riemannian and symplectic manifolds, characterized by differentiable structures enabling calculus-based analysis. Algebraic geometry focuses on algebraic varieties and schemes defined as solution sets of polynomial equations, incorporating complex, projective, and affine varieties with rich algebraic structure. While differential geometry revolves around smoothness and metric properties, algebraic geometry emphasizes the algebraic and topological properties of spaces defined over fields.
Applications in Mathematics and Physics
Differential geometry applies calculus and differential equations to study smooth shapes and curved spaces, playing a crucial role in the theory of general relativity and in modeling physical phenomena such as fluid dynamics and electromagnetism. Algebraic geometry investigates solutions to polynomial equations and their geometric properties, impacting number theory, cryptography, and string theory through the study of algebraic varieties and moduli spaces. Both fields intersect in areas like complex geometry and mirror symmetry, where differential structures and algebraic methods jointly advance research in mathematical physics.
Intersections and Interactions Between Both Fields
Differential geometry and algebraic geometry intersect notably in studying smooth manifolds and algebraic varieties, where differential geometric methods analyze local properties such as curvature while algebraic geometry explores global structures via polynomial equations. Techniques like sheaf theory and cohomology provide common ground for investigating singularities and moduli spaces, linking complex differential forms with algebraic invariants. This interplay enhances understanding of geometric objects through a blend of analytic and algebraic perspectives, crucial for advancements in areas like string theory and enumerative geometry.
Major Theorems and Results
Differential geometry centers on the study of smooth manifolds and their curvature properties, with landmark results such as the Gauss-Bonnet Theorem, which links topology and geometry by relating curvature to the Euler characteristic. Algebraic geometry explores solutions to polynomial equations and their geometric structures, epitomized by the Riemann-Roch Theorem, providing deep insights into the dimensions of spaces of sections of line bundles on algebraic curves. While differential geometry leverages analytical techniques to understand smooth shapes, algebraic geometry fundamentally relies on commutative algebra and scheme theory, exemplified by major advancements like the Hodge Decomposition Theorem that bridges both fields.
Future Directions and Open Problems
Differential geometry's future challenges include advancing the understanding of geometric flows and their applications in theoretical physics, particularly in quantum gravity and string theory. Algebraic geometry aims to deepen the study of moduli spaces and birational geometry while exploring connections with number theory via arithmetic geometry and mirror symmetry. Both fields anticipate progress in computational methods and interdisciplinary approaches, fostering breakthroughs in complex geometry and integrable systems.
Differential geometry Infographic
 libterm.com
libterm.com