A subgroup is a subset of a group that itself satisfies the group properties, including closure, associativity, identity, and invertibility under the same operation. Understanding the distinction between a subgroup and a generic subset is essential for grasping advanced concepts in group theory and algebraic structures. Explore the rest of the article to deepen your knowledge of how subgroups function within mathematical groups.
Table of Comparison
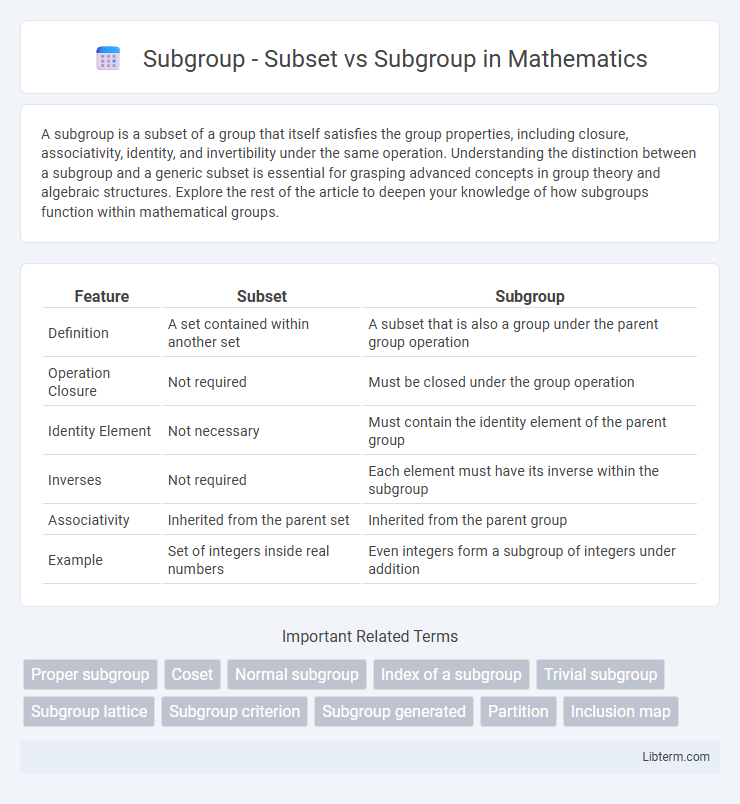
| Feature | Subset | Subgroup |
|---|---|---|
| Definition | A set contained within another set | A subset that is also a group under the parent group operation |
| Operation Closure | Not required | Must be closed under the group operation |
| Identity Element | Not necessary | Must contain the identity element of the parent group |
| Inverses | Not required | Each element must have its inverse within the subgroup |
| Associativity | Inherited from the parent set | Inherited from the parent group |
| Example | Set of integers inside real numbers | Even integers form a subgroup of integers under addition |
Understanding Subgroups: An Introduction
Understanding subgroups involves recognizing that every subgroup is a subset of a group, but not every subset qualifies as a subgroup. A subgroup must satisfy group axioms including closure, associativity, identity, and invertibility within the original group context, ensuring it itself forms a group. Distinguishing subgroups from arbitrary subsets is crucial for exploring group structure and symmetry in abstract algebra.
What Is a Subset?
A subset is a set whose elements are all contained within another set, meaning every member of the subset also belongs to the larger set. In mathematics, subsets can be proper or improper; a proper subset contains some but not all elements of the original set, while an improper subset is equal to the original set. Understanding subsets is fundamental in set theory, where they form the basis for defining other concepts like subgroups in algebra.
Defining a Subgroup
A subgroup is a subset of a group that itself satisfies all group axioms, including closure, associativity, identity, and inverses under the same binary operation. Unlike a generic subset, a subgroup must contain the identity element and be closed under the group operation and inverse operation. Defining a subgroup requires verifying these properties to ensure the subset inherits the group structure.
Key Differences Between Subsets and Subgroups
Subsets are collections containing some or all elements of a larger set, without additional structure, while subgroups are subsets of a group that themselves satisfy group axioms like closure, associativity, identity, and inverses. Key differences include that every subgroup is a subset, but not every subset qualifies as a subgroup due to the stricter algebraic conditions required. Subgroups maintain the group operation and identity, ensuring algebraic structure preservation, which subsets do not necessarily adhere to.
Criteria for a Subgroup
A subgroup is a subset of a group that itself satisfies the group axioms under the same operation, meaning it must contain the identity element, be closed under the group operation, and include inverses for every element. Unlike a general subset, which only requires membership in the original group, a subgroup must maintain the algebraic structure necessary to form a group independently. Verifying these criteria ensures the subset inherits the associative operation and forms a valid subgroup within the parent group.
Properties Unique to Subgroups
Subgroups are subsets of a group that satisfy the group axioms, including closure, associativity, identity, and inverses within the subset, making them groups themselves. Unlike general subsets, subgroups maintain the operation's structure intact, allowing for valid group operations restricted to the subset. The unique property of subgroups lies in their ability to inherit the group's algebraic structure, enabling analysis of symmetry and group behavior at a smaller scale.
Examples: Subsets vs Subgroups
Subsets include any selection of elements from a set, such as {1, 2} being a subset of {1, 2, 3}. Subgroups specifically refer to subsets of a group that themselves satisfy group properties like closure, identity, and inverses, for example, the even integers form a subgroup of the integers under addition. Unlike subsets that can be arbitrary collections, subgroups maintain the algebraic structure of the parent group.
Importance of Subgroups in Group Theory
Subgroups are subsets of a group that themselves satisfy the group axioms, playing a crucial role in understanding the structure of the entire group. Identifying subgroups allows mathematicians to analyze complex groups by breaking them into simpler, well-defined components, facilitating proofs and classification. The significance of subgroups is paramount in applications such as symmetry analysis, cryptography, and solving algebraic equations.
Common Mistakes: Subset or Subgroup?
Many learners confuse subsets with subgroups because both involve elements from a larger set, but subsets require only that elements belong to the set, while subgroups must satisfy additional algebraic properties such as closure, identity, and inverses under a group operation. A common mistake is assuming every subset of a group is a subgroup without verifying these properties, leading to incorrect conclusions in group theory. Understanding that all subgroups are subsets, but not all subsets are subgroups, is crucial for accurate mathematical reasoning and problem-solving.
Summary: Choosing Subset or Subgroup
Selecting a subset involves choosing any collection of elements from a set without necessarily preserving algebraic structure, whereas a subgroup must satisfy group properties such as closure, identity, and inverses within the original group. Subgroup selection ensures the subset operates under the same group operation, making it crucial for maintaining structural integrity in group theory applications. Choosing a subset is suitable for broader selections without algebraic constraints, while subgroups are essential for rigorous mathematical analysis and symmetry studies.
Subgroup - Subset Infographic
 libterm.com
libterm.com