Complete renovation projects transform outdated spaces into stunning, functional environments that enhance both comfort and value. Expert planning and quality materials ensure durability and aesthetic appeal tailored to your lifestyle. Explore the rest of the article to discover essential tips for a successful renovation.
Table of Comparison
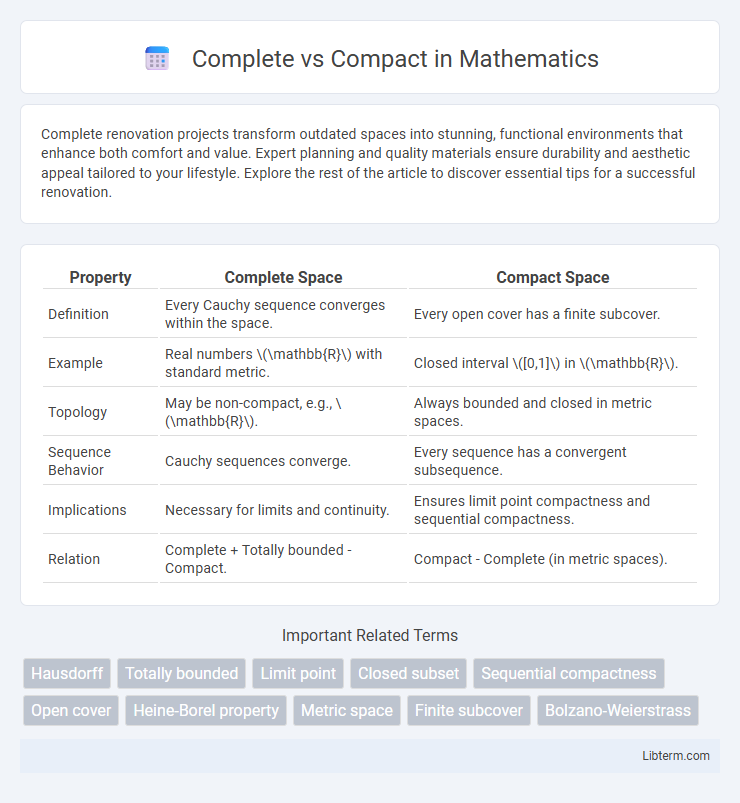
| Property | Complete Space | Compact Space |
|---|---|---|
| Definition | Every Cauchy sequence converges within the space. | Every open cover has a finite subcover. |
| Example | Real numbers \(\mathbb{R}\) with standard metric. | Closed interval \([0,1]\) in \(\mathbb{R}\). |
| Topology | May be non-compact, e.g., \(\mathbb{R}\). | Always bounded and closed in metric spaces. |
| Sequence Behavior | Cauchy sequences converge. | Every sequence has a convergent subsequence. |
| Implications | Necessary for limits and continuity. | Ensures limit point compactness and sequential compactness. |
| Relation | Complete + Totally bounded - Compact. | Compact - Complete (in metric spaces). |
Understanding Complete vs Compact: Key Definitions
Complete and Compact are key concepts in topology, where a Complete space ensures every Cauchy sequence converges within the space, guaranteeing no "gaps." Compactness means every open cover has a finite subcover, implying the space is limited and bounded in a topological sense. Understanding the distinction involves recognizing that completeness focuses on convergence properties, while compactness emphasizes covering and finiteness conditions.
Core Differences Between Complete and Compact
Complete systems encompass all necessary components and features, providing a full-fledged solution with extensive capabilities and flexibility. Compact systems prioritize minimalism and efficiency, offering a streamlined setup that conserves space and reduces complexity while focusing on essential functionalities. The core difference lies in the trade-off between comprehensive functionality in Complete systems and optimized simplicity in Compact designs.
Practical Examples: Complete vs Compact
Complete and compact data formats differ significantly in practical applications, notably in JSON and XML usage. Complete formats contain all possible elements and attributes, ensuring comprehensive data representation but increasing file size and complexity. Compact formats prioritize minimalism by excluding optional elements, reducing file size and enhancing transmission speed, making them ideal for bandwidth-sensitive environments.
Mathematical Implications and Applications
Complete metric spaces guarantee the convergence of every Cauchy sequence, which is crucial for solving equations and ensuring stability in numerical methods. Compact metric spaces extend these properties by ensuring every sequence has a convergent subsequence, enabling powerful results such as the Heine-Borel theorem and facilitating optimization and functional analysis. Applications span fixed-point theorems, partial differential equations, and machine learning algorithms that rely on completeness and compactness for convergence and generalization guarantees.
Topological Spaces: Where Complete and Compact Diverge
Complete topological spaces guarantee that every Cauchy sequence converges within the space, emphasizing metric completeness, whereas compact spaces ensure every open cover has a finite subcover, focusing on topological finiteness. In metric spaces, compactness implies completeness and total boundedness, but completeness alone does not require compactness, highlighting where these concepts diverge. The distinction is crucial in functional analysis and topology, affecting properties like continuity, convergence, and boundedness in various mathematical contexts.
Importance in Analysis and Topology
Complete metric spaces ensure the convergence of Cauchy sequences, which is crucial for rigorous analysis and the stability of solutions in topology. Compact spaces guarantee every open cover has a finite subcover, playing a vital role in continuity, convergence, and the compactness theorem critical for various topological proofs. Understanding the distinction and application of completeness versus compactness enhances the ability to analyze function behavior and topological structure effectively.
Visualizing Complete vs Compact Properties
Complete properties in topology ensure that every Cauchy sequence converges within the space, providing a solid foundation for continuous function analysis and metric space completeness. Compact properties imply that every open cover has a finite subcover, enabling finite approximations and powerful convergence results like the Heine-Borel theorem. Visualizing complete spaces often involves infinite limits and convergence behavior, while compact spaces emphasize containment and cover finiteness, critical for understanding boundedness and continuity in analysis.
Common Misconceptions Explained
Complete and compact sets often get confused due to overlapping characteristics, but they serve distinct purposes in topology and analysis. A complete set ensures every Cauchy sequence converges within the set, reinforcing internal consistency in metric spaces. Compact sets require every open cover to have a finite subcover, emphasizing finite approximability and often implying completeness in finite-dimensional spaces, though not vice versa.
Choosing Between Complete and Compact in Practice
Choosing between Complete and Compact collections depends primarily on the available storage space and data complexity needs. Complete collections offer full data representation suitable for detailed analysis, while Compact collections prioritize efficiency by storing only essential information. Practical application requires balancing thoroughness with resource constraints to optimize performance and usability.
Summary Table: Complete vs Compact at a Glance
The Summary Table: Complete vs Compact at a Glance highlights key differences in features, size, and performance efficiency. Complete models offer comprehensive capabilities with larger size and higher resource consumption, while Compact versions prioritize minimal footprint and streamlined functionality for optimized performance. This comparison aids in selecting the ideal solution based on specific operational needs and system constraints.
Complete Infographic
 libterm.com
libterm.com