Poisson manifolds generalize symplectic manifolds by allowing a Poisson bracket on the space of smooth functions, enabling the study of Hamiltonian dynamics in a broader context. They provide a rich geometric framework for integrating Lie algebras and understanding integrable systems. Discover how the structure of Poisson manifolds can deepen your insight into differential geometry and mathematical physics throughout this article.
Table of Comparison
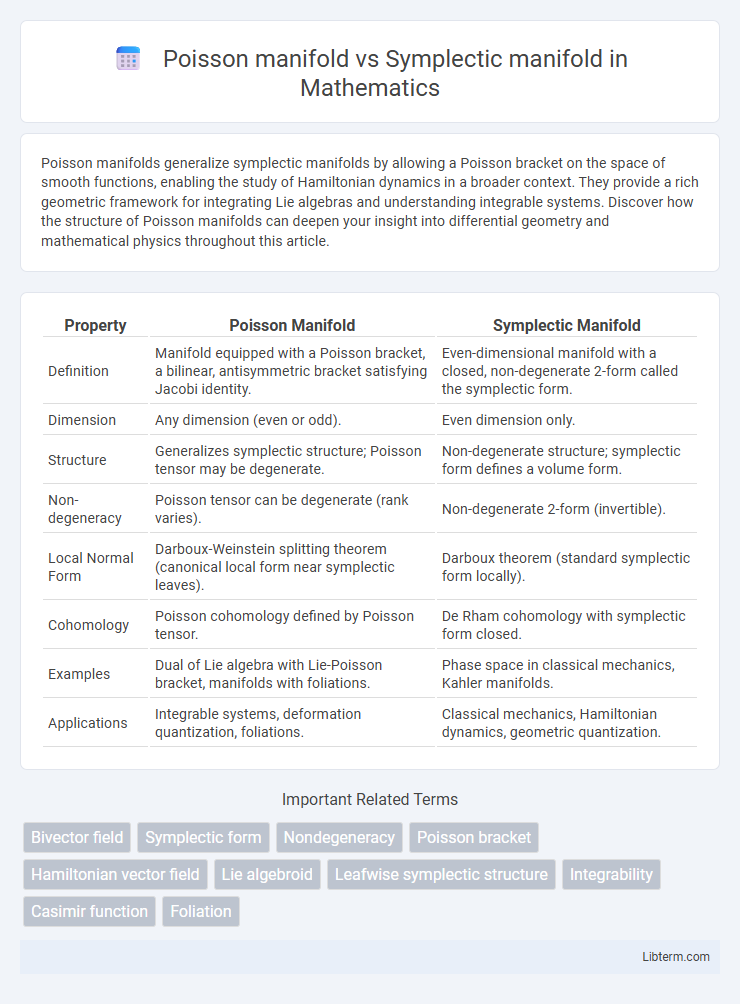
| Property | Poisson Manifold | Symplectic Manifold |
|---|---|---|
| Definition | Manifold equipped with a Poisson bracket, a bilinear, antisymmetric bracket satisfying Jacobi identity. | Even-dimensional manifold with a closed, non-degenerate 2-form called the symplectic form. |
| Dimension | Any dimension (even or odd). | Even dimension only. |
| Structure | Generalizes symplectic structure; Poisson tensor may be degenerate. | Non-degenerate structure; symplectic form defines a volume form. |
| Non-degeneracy | Poisson tensor can be degenerate (rank varies). | Non-degenerate 2-form (invertible). |
| Local Normal Form | Darboux-Weinstein splitting theorem (canonical local form near symplectic leaves). | Darboux theorem (standard symplectic form locally). |
| Cohomology | Poisson cohomology defined by Poisson tensor. | De Rham cohomology with symplectic form closed. |
| Examples | Dual of Lie algebra with Lie-Poisson bracket, manifolds with foliations. | Phase space in classical mechanics, Kahler manifolds. |
| Applications | Integrable systems, deformation quantization, foliations. | Classical mechanics, Hamiltonian dynamics, geometric quantization. |
Introduction to Poisson and Symplectic Manifolds
A Poisson manifold is a smooth manifold equipped with a Poisson bracket, a bilinear operation on smooth functions that generalizes the classical Poisson brackets in Hamiltonian mechanics, allowing for potentially degenerate or singular structures. Symplectic manifolds are a special subclass of Poisson manifolds where the Poisson bracket arises from a nondegenerate, closed 2-form called the symplectic form, providing a rich geometric framework ideal for classical mechanics. The key distinction lies in the nondegeneracy condition: all symplectic manifolds are Poisson manifolds with invertible Poisson tensors, while Poisson manifolds include more general cases with possibly degenerate Poisson structures leading to foliations into symplectic leaves.
Defining Poisson Structures: Fundamentals and Properties
Poisson manifolds generalize symplectic manifolds by allowing the Poisson bracket to be defined on a broader class of smooth manifolds without requiring nondegeneracy, characterized by a bivector field satisfying the Jacobi identity. Symplectic manifolds form a special case of Poisson manifolds with a nondegenerate, closed 2-form, ensuring that the Poisson structure is invertible and provides a canonical isomorphism between tangent and cotangent bundles. The fundamental property of a Poisson structure is the bilinearity, antisymmetry, and fulfillment of the Jacobi identity for the bracket operation on smooth functions, enabling a rich framework for Hamiltonian dynamics beyond symplectic geometry.
Symplectic Manifold Basics: Structure and Significance
A symplectic manifold is a smooth even-dimensional space equipped with a closed, non-degenerate 2-form called the symplectic form, which provides a geometric framework for classical mechanics. This structure ensures that symplectic manifolds are always orientable and possess an intrinsic volume form derived from the top wedge power of the symplectic form, playing a crucial role in Hamiltonian dynamics. Unlike Poisson manifolds, which allow degeneracies and singularities in their bracket structures, symplectic manifolds maintain a rigid, invertible structure that preserves canonical transformations and facilitates the study of conserved quantities and integrable systems.
Key Differences between Poisson and Symplectic Manifolds
Poisson manifolds generalize symplectic manifolds by allowing a Poisson bracket that may be degenerate, resulting in a possibly singular foliation into symplectic leaves, while symplectic manifolds possess a non-degenerate, closed 2-form defining a global symplectic structure. Unlike symplectic manifolds, Poisson manifolds lack a globally defined symplectic form, and their structure tensor is a bivector field satisfying the Jacobi identity, enabling more flexible geometric and algebraic properties. The dimension of symplectic manifolds is always even, whereas Poisson manifolds can have arbitrary dimension with variable rank of the Poisson tensor.
Geometric Interpretation: Poisson vs Symplectic
A Poisson manifold generalizes symplectic manifolds by allowing a bivector field that defines a bracket satisfying the Jacobi identity but may have varying rank, leading to a foliation into symplectic leaves. In contrast, a symplectic manifold possesses a non-degenerate, closed 2-form that induces a uniform symplectic structure on the entire manifold, ensuring a globally defined phase space geometry. The geometric interpretation highlights Poisson manifolds as stratified spaces with locally symplectic geometry, while symplectic manifolds maintain a consistent, globally non-degenerate geometric framework.
Examples of Poisson and Symplectic Manifolds
Poisson manifolds generalize symplectic manifolds by allowing the Poisson bracket to be degenerate, with examples including Lie-Poisson structures on duals of Lie algebras and products of symplectic manifolds with Poisson zero-brackets. Symplectic manifolds are a special class of Poisson manifolds characterized by non-degenerate, closed 2-forms, with classical examples such as the cotangent bundle of a smooth manifold and complex projective spaces equipped with the Fubini-Study form. These examples highlight the rigidity of symplectic structures and the broader flexibility of Poisson geometry in modeling constrained or singular phase spaces.
Morphisms and Mappings: Comparative Insights
Morphisms between Poisson manifolds are defined as smooth maps preserving the Poisson brackets, generalizing the symplectic structure preservation found in symplectic manifold morphisms, which require canonical transformations maintaining the nondegenerate closed 2-form. Poisson morphisms can map between manifolds of different dimensions, reflecting the potentially degenerate Poisson bivector, whereas symplectic morphisms are symplectomorphisms acting on manifolds of identical dimension due to the strict nondegeneracy condition. The flexibility of Poisson morphisms enables a broader category of geometric mappings crucial for understanding integrable systems and deformation quantization.
Applications in Physics and Mathematics
Poisson manifolds generalize symplectic manifolds by allowing degeneracies in the Poisson bracket, facilitating the study of Hamiltonian systems with constraints and singularities in classical mechanics. Symplectic manifolds provide the geometric framework for phase spaces in classical and quantum mechanics, crucial for formulating Hamiltonian dynamics and canonical transformations. In mathematics, Poisson geometry extends to integrable systems and deformation quantization, while symplectic topology underpins Floer homology and mirror symmetry theories.
Degeneracy and Non-Degeneracy: Core Distinctions
A Poisson manifold generalizes a symplectic manifold by allowing a Poisson bracket defined by a bivector field that may be degenerate, meaning its rank can vary and vanish at some points, causing the structure to fail to be invertible everywhere. In contrast, a symplectic manifold has a non-degenerate, closed 2-form that induces a constant rank and an invertible Poisson bivector, ensuring a canonical isomorphism between tangent and cotangent bundles. This fundamental difference highlights the degeneracy flexibility in Poisson manifolds versus the strict non-degeneracy condition essential to symplectic geometry.
Conclusion: Choosing between Poisson and Symplectic Structures
Choosing between Poisson and symplectic structures depends on the underlying geometric and physical context; symplectic manifolds provide a nondegenerate, closed 2-form ideal for classical Hamiltonian mechanics, ensuring rigid structure and invertibility. Poisson manifolds generalize this framework with potentially degenerate brackets, allowing singularities and more flexibility, suitable for systems with constraints or varying symplectic leaves. The decision hinges on whether a global symplectic form exists or only a Poisson structure accommodating local symplectic geometry is required.
Poisson manifold Infographic
 libterm.com
libterm.com