The unit impulse function, also known as the Dirac delta function, is a fundamental concept in signal processing and control systems, characterized by its zero value everywhere except at zero, where it is infinitely high, with an integral of one. It is essential for analyzing system responses and serves as a mathematical tool to model instantaneous impacts or signals in time. Discover how the unit impulse function plays a critical role in various applications throughout this article.
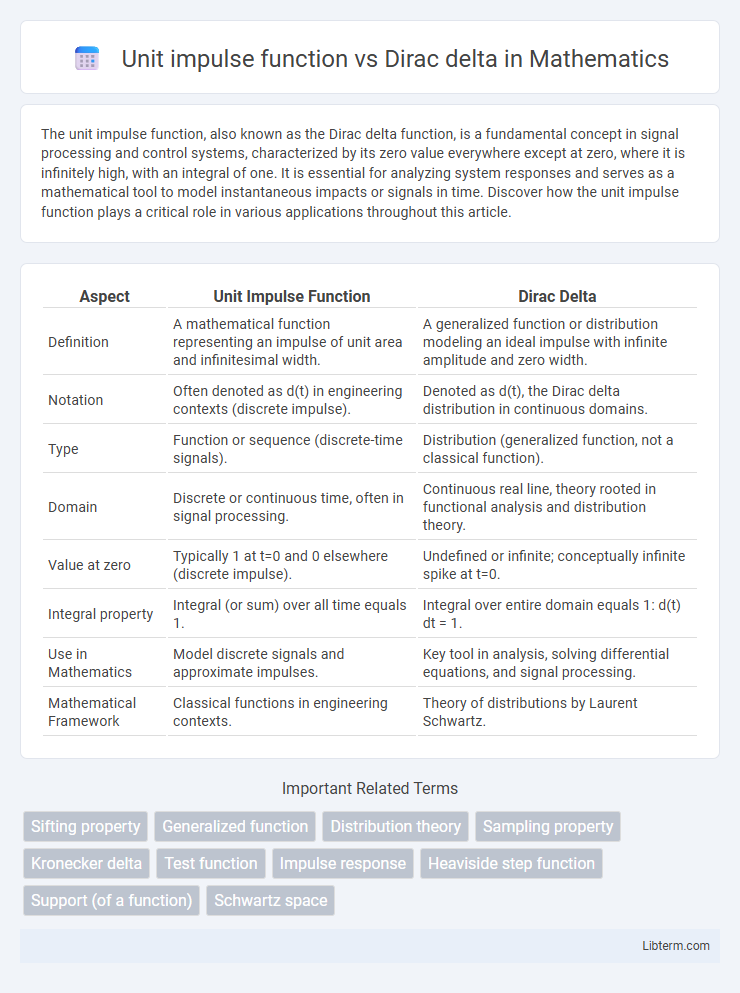
Table of Comparison
| Aspect | Unit Impulse Function | Dirac Delta |
|---|---|---|
| Definition | A mathematical function representing an impulse of unit area and infinitesimal width. | A generalized function or distribution modeling an ideal impulse with infinite amplitude and zero width. |
| Notation | Often denoted as d(t) in engineering contexts (discrete impulse). | Denoted as d(t), the Dirac delta distribution in continuous domains. |
| Type | Function or sequence (discrete-time signals). | Distribution (generalized function, not a classical function). |
| Domain | Discrete or continuous time, often in signal processing. | Continuous real line, theory rooted in functional analysis and distribution theory. |
| Value at zero | Typically 1 at t=0 and 0 elsewhere (discrete impulse). | Undefined or infinite; conceptually infinite spike at t=0. |
| Integral property | Integral (or sum) over all time equals 1. | Integral over entire domain equals 1: d(t) dt = 1. |
| Use in Mathematics | Model discrete signals and approximate impulses. | Key tool in analysis, solving differential equations, and signal processing. |
| Mathematical Framework | Classical functions in engineering contexts. | Theory of distributions by Laurent Schwartz. |
Introduction to Unit Impulse Function and Dirac Delta
The unit impulse function, often represented as d(t), is a fundamental concept in signal processing and systems analysis, characterized by an infinitely high peak at t = 0 and an area of one under its curve. The Dirac delta, a generalized function introduced by physicist Paul Dirac, serves as a mathematical model for an idealized impulse with zero width and unit area, enabling simplified analysis of linear time-invariant systems. Both concepts are essential for understanding impulse responses and are widely used in engineering, physics, and applied mathematics to model instantaneous events.
Mathematical Definitions
The unit impulse function, often represented as d(t), is mathematically defined as a limit of a sequence of functions that approaches zero everywhere except at t = 0, where its integral equals one. The Dirac delta function is a generalized function or distribution that formalizes this concept, characterized by the sifting property f(t) d(t - t0) dt = f(t0). Both serve as idealized representations of instantaneous impulses in systems, essential in signal processing and differential equations.
Historical Origins
The Dirac delta function was introduced by physicist Paul Dirac in the 1930s as a mathematical tool to model point charges and mass distributions in quantum mechanics. The unit impulse function, closely related, originated in engineering and signal processing to represent an instantaneous pulse with an integral equal to one. Both concepts evolved to bridge theoretical physics and practical applications in systems analysis.
Key Properties and Characteristics
The Unit Impulse Function and the Dirac Delta are foundational in signal processing and system analysis, both representing an idealized pulse with zero duration and infinite amplitude, but their interpretations differ: the Unit Impulse is a discrete sequence impulse with a value of one at zero and zero elsewhere, while the Dirac Delta is a continuous distribution used in integral transforms. Key properties include the sifting property, where the integral of a function multiplied by the Dirac Delta yields the function's value at zero, and the Unit Impulse's role as the identity element under convolution in discrete-time systems. The Dirac Delta's representation as a generalized function or distribution enables rigorous handling in continuous-time frameworks, whereas the Unit Impulse is primarily applied in discrete-time signal models.
Graphical Representation
The unit impulse function and Dirac delta are often represented graphically as an infinitely high, narrow spike at t=0 with an area under the curve equal to one, symbolizing their integral property. While the unit impulse is a theoretical function used in discrete-time systems, the Dirac delta is a distribution employed in continuous-time signal analysis. Graphs typically depict the Dirac delta as an arrow on the time axis pointing upward at zero, emphasizing its role as an idealized impulse with no width but unit area.
Differences Between Unit Impulse and Dirac Delta
The Unit impulse function, often represented as a rectangular pulse with finite height and duration, differs from the Dirac delta, which is an idealized mathematical distribution characterized by an infinite peak at zero width and unit area. Unlike the Unit impulse, the Dirac delta function cannot be expressed as a conventional function but serves as a generalized function used primarily in continuous-time signal analysis and system modeling. The key distinction lies in the Dirac delta's role as a limit of narrowing unit impulses with constant area, making it indispensable for sampling and convolution operations in engineering and physics.
Applications in Engineering and Physics
The unit impulse function and Dirac delta are fundamental in signal processing and system analysis, with the Dirac delta representing an idealized point impulse used in modeling instantaneous events in physics and engineering. In control systems, the unit impulse function allows engineers to analyze system response and stability by simulating sudden forces or shocks. In quantum mechanics and electromagnetic theory, the Dirac delta facilitates the handling of point charges and mass distributions, enabling precise mathematical modeling of localized phenomena.
Role in Signal Processing
The Unit impulse function, often represented as u(t), serves as a fundamental signal for testing linear systems due to its step-like nature, enabling the examination of system response over time. The Dirac delta function, d(t), acts as an idealized impulse with infinite amplitude and zero width, serving as a critical tool for sampling and analyzing continuous-time signals in signal processing. Both functions are essential in system characterization, with d(t) providing precise localization in time while u(t) offers insight into cumulative system behavior.
Common Misconceptions
The unit impulse function is often mistaken as a regular function, whereas the Dirac delta is a distribution that models an idealized point impulse with infinite magnitude and zero duration. A common misconception is treating the Dirac delta as a function with a specific value at zero instead of understanding it as an operator that extracts the value of another function at a point. Confusing the unit impulse with finite-area pulses leads to errors in signal processing and system analysis where precise interpretation of impulsive behavior is critical.
Summary and Conclusions
The Unit impulse function and the Dirac delta are closely related concepts used in signal processing and systems analysis, where the Unit impulse function serves as an idealized representation of an instantaneous impulse with unit area under the curve. The Dirac delta is a generalized function or distribution that models this ideal impulse, enabling mathematical operations involving integral and convolution in continuous-time signals. Both functions are fundamental in analyzing linear time-invariant (LTI) systems due to their ability to isolate system responses, but the Dirac delta provides a more rigorous framework for theoretical and practical applications through distribution theory.
Unit impulse function Infographic
 libterm.com
libterm.com