A semisimple group is a type of Lie group characterized by having a Lie algebra that is a direct sum of simple Lie algebras, which means it contains no abelian ideals other than zero. These groups play a crucial role in many areas of mathematics and theoretical physics due to their well-structured symmetry properties and representation theory. Explore the rest of the article to understand how semisimple groups influence modern algebra and geometry.
Table of Comparison
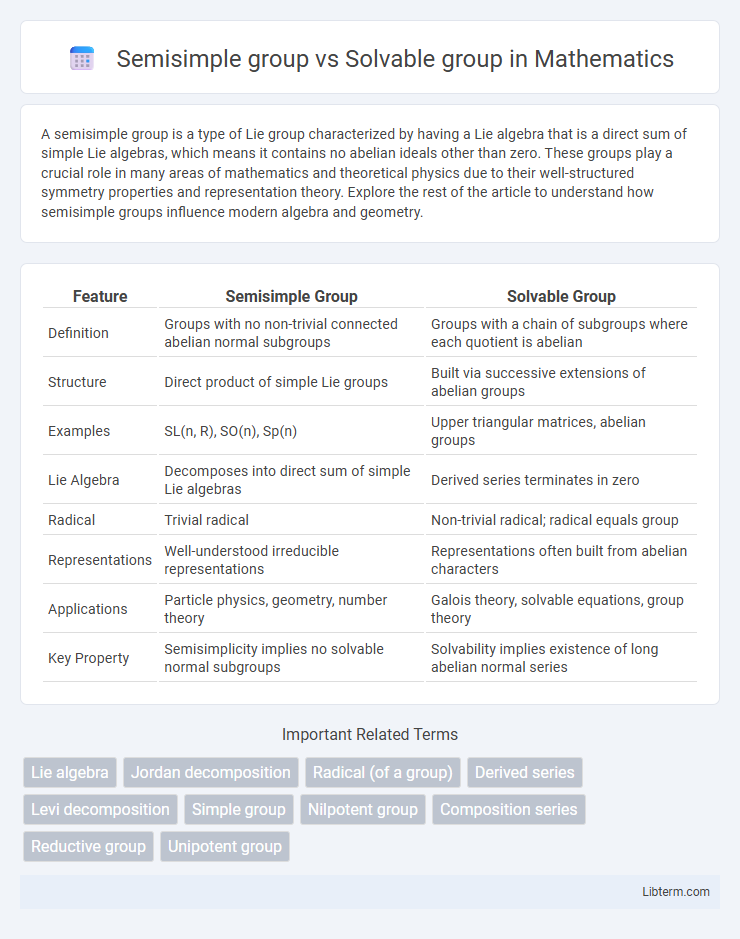
| Feature | Semisimple Group | Solvable Group |
|---|---|---|
| Definition | Groups with no non-trivial connected abelian normal subgroups | Groups with a chain of subgroups where each quotient is abelian |
| Structure | Direct product of simple Lie groups | Built via successive extensions of abelian groups |
| Examples | SL(n, R), SO(n), Sp(n) | Upper triangular matrices, abelian groups |
| Lie Algebra | Decomposes into direct sum of simple Lie algebras | Derived series terminates in zero |
| Radical | Trivial radical | Non-trivial radical; radical equals group |
| Representations | Well-understood irreducible representations | Representations often built from abelian characters |
| Applications | Particle physics, geometry, number theory | Galois theory, solvable equations, group theory |
| Key Property | Semisimplicity implies no solvable normal subgroups | Solvability implies existence of long abelian normal series |
Introduction to Group Theory
Semisimple groups are algebraic groups characterized by having no nontrivial connected solvable normal subgroups, making their structure robust and resistant to simplification. Solvable groups, on the other hand, possess a series of subgroups leading to the trivial group, where each quotient is abelian, reflecting a hierarchical and decomposable structure. In group theory, understanding the distinction between semisimple and solvable groups is crucial for analyzing symmetry, representation theory, and the classification of algebraic groups.
Defining Semisimple Groups
Semisimple groups are algebraic groups characterized by having trivial radical, meaning they contain no nontrivial connected solvable normal subgroups, which distinguishes them sharply from solvable groups defined by their ability to be decomposed through a series of Abelian quotient groups. The defining property of semisimple groups lies in their Lie algebra being a direct sum of simple Lie algebras, reflecting a rich structure with no nonzero abelian ideals. This structural difference makes semisimple groups central in representation theory and algebraic geometry, where their rigid and non-solvable nature contrasts with the progressively decomposable nature of solvable groups.
Characteristics of Solvable Groups
Solvable groups are characterized by a chain of normal subgroups whose successive quotients are abelian, reflecting a stepwise decomposition into simpler components. These groups typically have a derived series terminating in the trivial subgroup, highlighting their hierarchical commutator structure. In contrast, semisimple groups lack such a solvable structure, often featuring more complex representations and richer algebraic properties.
Structural Differences between Semisimple and Solvable Groups
Semisimple groups possess a structure characterized by the decomposition into simple, non-abelian subgroups with no nontrivial solvable normal subgroups, distinguishing them from solvable groups that have a finite derived series terminating in the trivial subgroup. The absence of abelian or nilpotent factors in semisimple groups contrasts sharply with solvable groups, which are constructed through successive extensions of abelian groups. This fundamental structural difference impacts classification, representation theory, and the behavior of these groups in algebraic and geometric contexts.
Examples of Semisimple Groups
Semisimple groups are algebraic or Lie groups characterized by a trivial radical, making their structure fully reducible and without abelian normal subgroups. Examples of semisimple groups include classical matrix groups like SL(n, R), SO(n), and Sp(2n), each representing special linear, orthogonal, and symplectic groups respectively. These groups contrast with solvable groups such as the group of upper triangular matrices, which have a series of abelian normal subgroups and are inherently non-semisimple.
Examples of Solvable Groups
Solvable groups include important examples such as abelian groups, where the commutator subgroup is trivial, and the group of upper triangular matrices with nonzero diagonal entries, which is metabelian. The symmetric group S_3 is another classic example of a solvable group, as it has a normal subgroup of order 3 with an abelian quotient of order 2. In contrast, semisimple groups, like SL(2, R), typically have no nontrivial solvable normal subgroups and exhibit more complex structures related to Lie algebras.
Importance in Algebra and Representation Theory
Semisimple groups play a crucial role in algebra and representation theory due to their well-structured decomposition into simple groups, enabling the classification of representations via highest weight theory and complete reducibility of modules. Solvable groups are significant for understanding the structure of more complex groups, as their composition series with abelian factors facilitate the application of Lie's and Lie-Kolchin theorems in representation theory. The dichotomy between semisimple and solvable groups underpins the classification of algebraic groups and informs the study of symmetry in mathematical physics and geometry.
Applications of Semisimple and Solvable Groups
Semisimple groups are extensively used in particle physics and theoretical chemistry for modeling symmetries of fundamental particles and molecular structures, as their representation theory provides tools for understanding invariant properties. Solvable groups find critical applications in Galois theory, aiding in the classification of polynomial equations by their solvability through radicals, as well as in cryptography for constructing algebraic algorithms with predictable complexity. Both group types contribute to differential geometry and control theory, where semisimple groups assist in analyzing Lie algebras related to continuous symmetries, and solvable groups help model systems with hierarchical or decomposable symmetry structures.
Key Theorems Distinguishing Semisimple and Solvable Groups
Semisimple groups are characterized by the Levi decomposition theorem, which states every connected Lie group has a semisimple Lie algebra as a direct sum complement to its radical, distinguishing them from solvable groups whose Lie algebra consists entirely of solvable subalgebras. The Lie-Kolchin theorem asserts that every connected, solvable linear algebraic group over an algebraically closed field has a triangularizable representation, a property not shared by semisimple groups, reflecting their fundamentally different structure. The absence of nontrivial abelian normal subgroups in semisimple groups contrasts with solvable groups, which are built through a series of abelian normal subgroups, highlighting their divergent algebraic and representation-theoretic features.
Conclusion: Comparing Semisimple and Solvable Groups
Semisimple groups are characterized by their decomposability into simple non-abelian components with no nontrivial solvable normal subgroups, whereas solvable groups have a derived series terminating in the trivial subgroup, reflecting an inherently hierarchical and abelian structure. The distinct algebraic properties imply semisimple groups are often linked to complex symmetries in Lie theory and geometry, while solvable groups appear prominently in Galois theory and the solution of polynomial equations by radicals. Understanding these differences is crucial for applications in representation theory, algebraic group classification, and the structural analysis of differential equations.
Semisimple group Infographic
 libterm.com
libterm.com