Vector space is a fundamental concept in linear algebra, consisting of a collection of vectors that can be added together and multiplied by scalars while satisfying specific axioms. Understanding vector spaces allows you to analyze geometric and algebraic structures in physics, computer science, and engineering. Explore the rest of the article to dive deeper into the properties and applications of vector spaces.
Table of Comparison
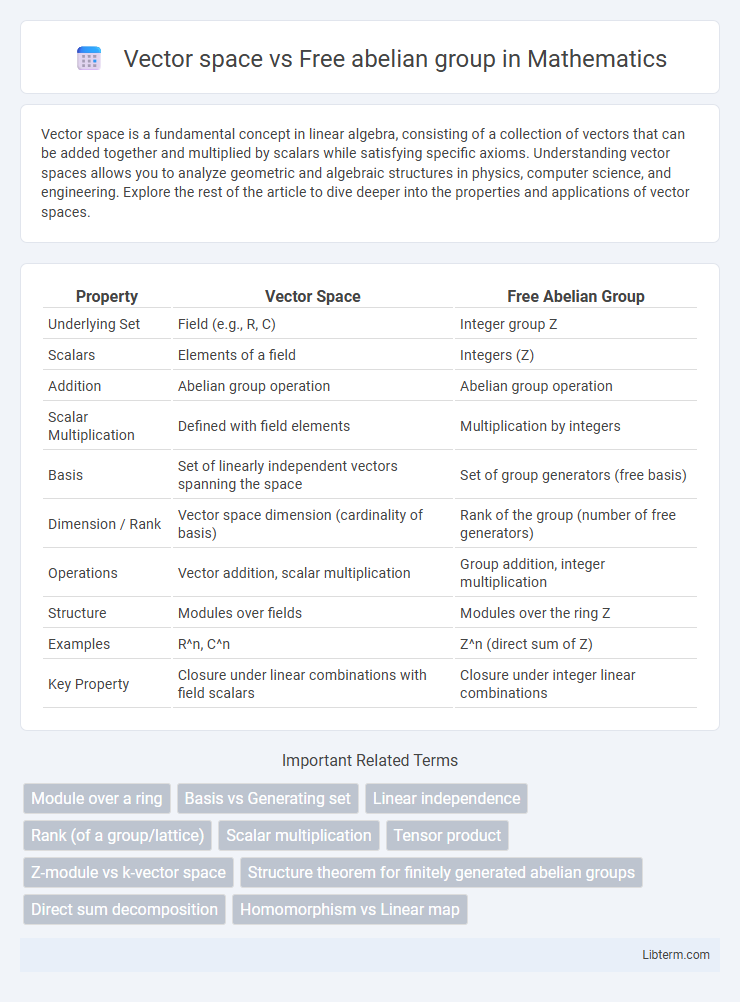
| Property | Vector Space | Free Abelian Group |
|---|---|---|
| Underlying Set | Field (e.g., R, C) | Integer group Z |
| Scalars | Elements of a field | Integers (Z) |
| Addition | Abelian group operation | Abelian group operation |
| Scalar Multiplication | Defined with field elements | Multiplication by integers |
| Basis | Set of linearly independent vectors spanning the space | Set of group generators (free basis) |
| Dimension / Rank | Vector space dimension (cardinality of basis) | Rank of the group (number of free generators) |
| Operations | Vector addition, scalar multiplication | Group addition, integer multiplication |
| Structure | Modules over fields | Modules over the ring Z |
| Examples | R^n, C^n | Z^n (direct sum of Z) |
| Key Property | Closure under linear combinations with field scalars | Closure under integer linear combinations |
Introduction to Vector Spaces and Free Abelian Groups
Vector spaces are algebraic structures consisting of vectors that can be scaled and added following field properties, enabling linear combinations over a field such as the real numbers. Free abelian groups are groups generated by a set where every element can be uniquely expressed as an integer linear combination of generators, emphasizing integer coefficients instead of field elements. Unlike vector spaces that rely on scalar multiplication from a field, free abelian groups focus purely on additive group operations with integer coefficients, forming a foundational concept in algebraic topology and group theory.
Fundamental Definitions and Structures
A vector space is a collection of vectors equipped with two operations: vector addition and scalar multiplication by elements from a field, satisfying axioms like associativity, commutativity, and distributivity. A free abelian group consists of elements generated by a basis set with integer coefficients and includes operations of addition and inverse, emphasizing group structure without scalar multiplication. The key structural difference lies in scalar fields for vector spaces versus integer coefficients for free abelian groups, influencing their algebraic properties and applications.
Basis and Generating Sets Compared
A vector space basis consists of a linearly independent set that spans the entire space, allowing every vector to be uniquely expressed as a finite linear combination of basis vectors with coefficients in a field. In contrast, a free abelian group has a generating set where every element is a unique finite integer linear combination of basis elements, emphasizing integral coefficients and abelian group structure rather than scalar multiplication in a field. The key distinction lies in vector space bases requiring linear independence over a field, while free abelian groups involve independence under integer linear combinations, impacting the nature and application of their generating sets.
Operations: Addition and Scalar Multiplication
Vector spaces involve addition and scalar multiplication defined over a field, allowing operations such as vector scaling by any element of that field to produce another vector in the space. In contrast, free abelian groups operate with an addition operation only, where group elements combine according to integer coefficients, lacking scalar multiplication by arbitrary field elements. This difference highlights that free abelian groups are modules over the integers, limiting scalar multiplication to integer values, whereas vector spaces support a broader range of scalars from the underlying field.
Underlying Fields vs. Rings
Vector spaces are defined over underlying fields, which provide commutative multiplication with multiplicative inverses, enabling scalar multiplication that satisfies linearity and invertibility properties. Free abelian groups, on the other hand, are modules over the ring of integers \( \mathbb{Z} \), a commutative ring without multiplicative inverses, which restricts scalar multiplication to integer coefficients only. This fundamental difference in underlying algebraic structures governs the behavior of scalar multiplication and the types of linear combinations possible in vector spaces versus free abelian groups.
Homomorphisms and Linear Maps
Homomorphisms between free abelian groups correspond to group homomorphisms preserving the abelian structure, often represented by integer matrices, while linear maps between vector spaces over a field require preserving scalar multiplication and addition, represented by matrices over that field. The kernel and image of a vector space linear map are subspaces, while for free abelian groups, they are subgroups, reflecting differences in structure and dimension theory. Scalar multiplication in vector spaces introduces linear independence and basis concepts absent in free abelian group homomorphisms, influencing the classification and analysis of these maps.
Finite-dimensional vs. Infinite-dimensional Cases
Finite-dimensional vector spaces over a field share a structural analogy with free abelian groups of finite rank, as both admit a finite basis allowing unique linear or integral combinations. Infinite-dimensional vector spaces extend this framework with bases of infinite cardinality, paralleling free abelian groups of infinite rank, where the notion of dimension or rank becomes a cardinal invariant. The dimensionality in vector spaces and rank in free abelian groups govern the complexity and type of linear independence, basis selection, and module theoretic properties within algebraic structures.
Applications in Algebra and Geometry
Vector spaces serve as foundational structures in algebra and geometry, enabling the study of linear transformations, eigenvalues, and eigenvectors that underpin systems of linear equations and geometric transformations. Free abelian groups, characterized by their basis elements with integer coefficients, are crucial in algebraic topology and homological algebra for analyzing topological spaces through homology groups and chain complexes. The distinction between vector spaces over fields and free abelian groups over the integers highlights different algebraic properties applied in classifying geometric objects and solving problems in group cohomology and lattice theory.
Key Differences and Similarities
Vector spaces consist of vectors that can be scaled by elements from a field, enabling linear combinations with scalar multiplication and vector addition. Free abelian groups are composed of elements with addition, where each element can be uniquely expressed as an integer linear combination of basis elements, but lack scalar multiplication by arbitrary field elements. Both structures have a basis allowing unique representation of elements, yet vector spaces support richer algebraic operations due to field-based scalars, distinguishing them significantly from free abelian groups which are modules over the integers.
Summary and Conclusion
Vector spaces consist of a set equipped with operations of vector addition and scalar multiplication over a field, providing a structure that supports linear combinations and dimensional analysis. Free abelian groups, constructed as the direct sum of copies of the integers \(\mathbb{Z}\), focus on additive group operations without scalar multiplication, emphasizing generators and relations within an integral domain. The key distinction lies in the presence of scalar multiplication in vector spaces, enabling richer algebraic properties, whereas free abelian groups serve as foundational tools in algebraic topology and combinatorial group theory due to their simpler, torsion-free additive structure.
Vector space Infographic
 libterm.com
libterm.com