Monoidal categories provide a framework to study tensor-like structures in abstract mathematics, enabling the combination of objects and morphisms with an associative binary operation and an identity object. This concept plays a crucial role in areas such as algebra, topology, and theoretical computer science, linking category theory with practical applications. Explore the rest of the article to deepen your understanding of monoidal categories and their significance across different mathematical fields.
Table of Comparison
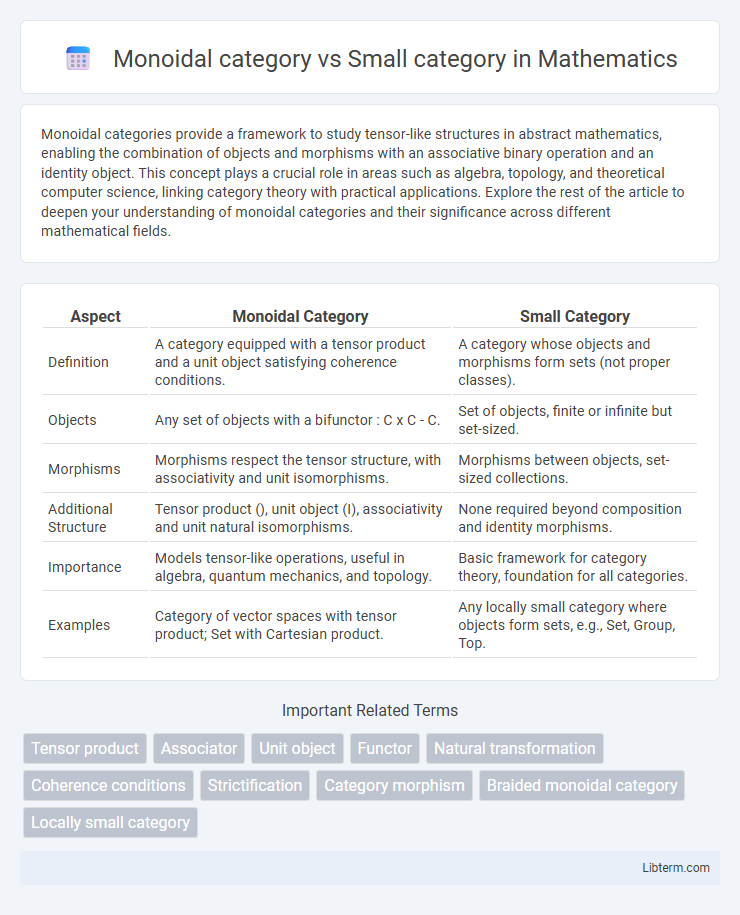
| Aspect | Monoidal Category | Small Category |
|---|---|---|
| Definition | A category equipped with a tensor product and a unit object satisfying coherence conditions. | A category whose objects and morphisms form sets (not proper classes). |
| Objects | Any set of objects with a bifunctor : C x C - C. | Set of objects, finite or infinite but set-sized. |
| Morphisms | Morphisms respect the tensor structure, with associativity and unit isomorphisms. | Morphisms between objects, set-sized collections. |
| Additional Structure | Tensor product (), unit object (I), associativity and unit natural isomorphisms. | None required beyond composition and identity morphisms. |
| Importance | Models tensor-like operations, useful in algebra, quantum mechanics, and topology. | Basic framework for category theory, foundation for all categories. |
| Examples | Category of vector spaces with tensor product; Set with Cartesian product. | Any locally small category where objects form sets, e.g., Set, Group, Top. |
Introduction to Monoidal Categories and Small Categories
Monoidal categories generalize small categories by equipping them with a tensor product operation and a unit object, providing a framework to handle objects and morphisms with a notion of multiplication and identity. Small categories are foundational structures with sets of objects and morphisms, whereas monoidal categories extend this by adding coherence conditions for associativity and unit constraints. The introduction to monoidal categories emphasizes their role in tensor calculus, quantum algebra, and theoretical computer science, contrasting with small categories' focus on basic morphism composition and identity elements.
Basic Definitions: Monoidal Category vs Small Category
A monoidal category is a category equipped with a tensor product, an identity object, and natural isomorphisms satisfying coherence conditions that enable the manipulation of objects and morphisms in a way analogous to multiplication and identity in algebra. A small category is defined by having a set (rather than a proper class) of objects and morphisms, emphasizing size constraints rather than additional structure. While small categories focus on the cardinality of their collections, monoidal categories enrich categorical structure by introducing a bifunctor and unit object that obey associativity and unit laws.
Structural Components: Objects, Morphisms, and Functors
Monoidal categories consist of objects and morphisms equipped with a tensor product, associativity constraint, and a unit object, enhancing the basic structure found in small categories. Small categories have a set (as opposed to a class) of objects and morphisms with composition and identity, forming the foundational framework for category theory. Functors between monoidal categories preserve the tensor product and unit object, whereas functors between small categories focus solely on maintaining composition and identity mappings.
Associativity and Unit Constraints in Monoidal Categories
Monoidal categories extend small categories by introducing a tensor product operation that combines objects and morphisms, governed by associativity and unit constraints expressed through natural isomorphisms. The associativity constraint ensures that the tensor product is associative up to a specified isomorphism, making the diagram involving triple tensors commute, while the unit constraints establish a designated unit object acting neutrally with respect to the tensor product. These coherence conditions differentiate monoidal categories from small categories, where associativity and identity components hold strictly without such flexible natural isomorphisms.
Size Considerations: Smallness and Set-Theoretical Issues
Small categories are defined by having a set of objects and morphisms, ensuring manageable size within standard set theory, while monoidal categories impose additional structure through a tensor product that may increase complexity without necessarily restricting size. Size considerations arise because forming monoidal structures often involves products or constructions that can lead to proper classes, complicating foundational issues in category theory. Addressing set-theoretical issues typically requires working within a suitable universe or employing Grothendieck universes to maintain control over size and ensure the coherence of monoidal categories.
Monoidal Categories: Tensor Product and Identity Object
Monoidal categories feature a tensor product, a bifunctor that combines objects and morphisms, enriching the categorical structure beyond that of small categories which primarily involve objects and morphisms without additional operations. The identity object in a monoidal category acts as a neutral element for the tensor product, analogous to the role of an identity element in algebraic structures, ensuring coherence and associativity through natural isomorphisms. These structures facilitate the modeling of parallel composition and resource combination, making monoidal categories fundamental in areas such as algebra, topology, and theoretical computer science.
Examples: Typical Monoidal and Small Categories
Typical examples of monoidal categories include the category of vector spaces over a field, equipped with the tensor product as the monoidal operation, and the category of sets with Cartesian product as the monoidal structure. Small categories often serve as foundational examples, such as the category with finite sets and functions, or posets viewed as categories with a small number of objects and morphisms reflecting order relations. The distinction lies in monoidal categories having an additional tensor product structure compatible with associativity and unit constraints, while small categories are primarily concerned with size limitations of objects and morphisms.
Functorial Perspectives: Mapping Between Categories
A monoidal category enhances a small category by equipping it with a tensor product and a unit object, enabling the functorial mapping to preserve both morphisms and the monoidal structure. Functors between monoidal categories, called monoidal functors, must maintain the coherence conditions involving tensoring and unit objects, extending the basic functorial requirements observed in small categories. In contrast, functors between small categories only need to map objects and morphisms while preserving composition and identities without considering additional tensorial structures.
Applications in Mathematics and Theoretical Computer Science
Monoidal categories provide a framework for tensor products and have applications in quantum computing, category theory, and higher algebra, enabling the modeling of parallel processes and resource management. Small categories, defined by having a set (rather than a proper class) of objects and morphisms, are fundamental in the study of categorical structures, type theory, and database theory. In theoretical computer science, monoidal categories underpin the semantics of programming languages and process calculi, while small categories facilitate formalizing domain-specific languages and data transformations.
Comparative Summary: Key Differences and Similarities
A monoidal category extends the structure of a small category by incorporating a tensor product and a unit object, enabling the expression of parallel composition alongside morphisms' sequential composition. Small categories emphasize a set-sized collection of objects and morphisms without additional monoidal structure, making them foundational in category theory. Both share the foundational concepts of objects, morphisms, and composition, but monoidal categories enrich this framework by introducing coherence conditions related to associativity and identity in tensor operations.
Monoidal category Infographic
 libterm.com
libterm.com