Commutative algebra focuses on the study of commutative rings and their ideals, modules, and algebraic structures. It forms the foundation for algebraic geometry and number theory by exploring properties like prime ideals, localization, and integral extensions. Dive deeper into this article to understand how commutative algebra shapes modern mathematical theories and applications relevant to your studies.
Table of Comparison
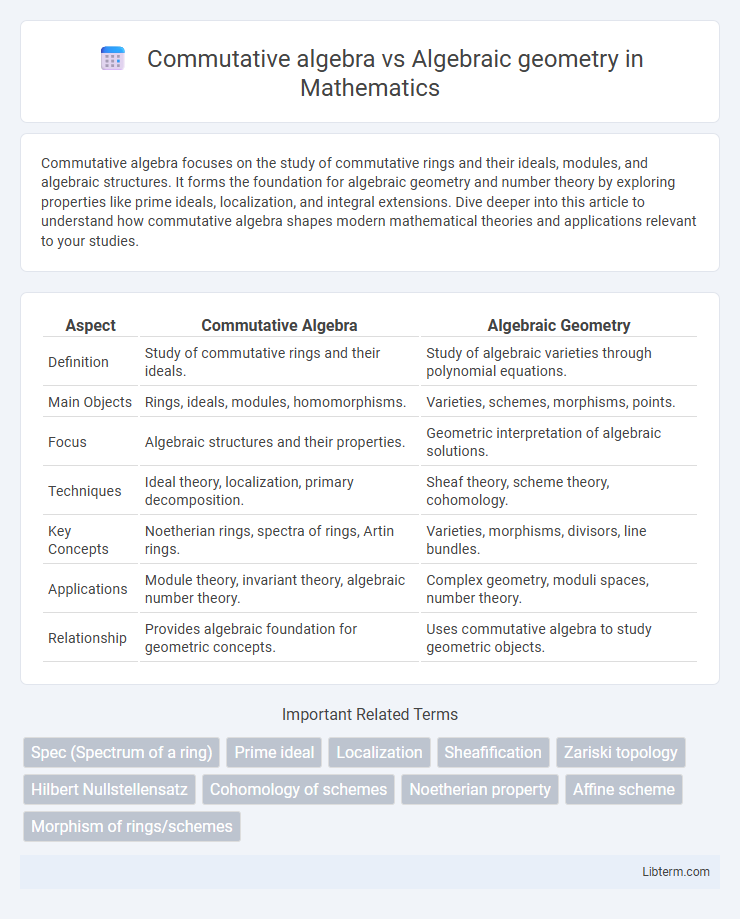
| Aspect | Commutative Algebra | Algebraic Geometry |
|---|---|---|
| Definition | Study of commutative rings and their ideals. | Study of algebraic varieties through polynomial equations. |
| Main Objects | Rings, ideals, modules, homomorphisms. | Varieties, schemes, morphisms, points. |
| Focus | Algebraic structures and their properties. | Geometric interpretation of algebraic solutions. |
| Techniques | Ideal theory, localization, primary decomposition. | Sheaf theory, scheme theory, cohomology. |
| Key Concepts | Noetherian rings, spectra of rings, Artin rings. | Varieties, morphisms, divisors, line bundles. |
| Applications | Module theory, invariant theory, algebraic number theory. | Complex geometry, moduli spaces, number theory. |
| Relationship | Provides algebraic foundation for geometric concepts. | Uses commutative algebra to study geometric objects. |
Introduction to Commutative Algebra and Algebraic Geometry
Commutative algebra provides the foundational language and tools for understanding algebraic structures like rings and modules, essential for the study of algebraic geometry, which explores geometric objects defined by polynomial equations. The introduction to commutative algebra typically covers concepts such as ideals, prime ideals, localization, and modules, establishing a framework for interpreting varieties and schemes in algebraic geometry. Algebraic geometry extends these notions by investigating the geometric properties and structures emerging from commutative rings, linking algebraic and topological perspectives in a profound way.
Fundamental Concepts: Rings, Ideals, and Varieties
Commutative algebra centers on the study of rings and ideals, providing an algebraic framework for analyzing polynomial equations and their solutions. Algebraic geometry builds on this foundation by exploring varieties, which are geometric manifestations of solutions to systems of polynomial equations defined by ideals in rings. The interplay between the algebraic structure of rings and ideals and the geometric properties of varieties forms the core of both disciplines, enabling deep insights into both algebraic and geometric problems.
Historical Development of Both Fields
Commutative algebra originated in the early 20th century through the foundational work of mathematicians like Emmy Noether, who formalized the study of rings and ideals, shaping modern algebraic structures. Algebraic geometry evolved from classical geometry and algebra, with significant advancements in the mid-20th century due to Grothendieck's introduction of schemes, which connected geometric objects with commutative algebra. The interplay between these fields deepened over time, as commutative algebra provided the rigorous algebraic tools necessary for the development of modern algebraic geometry.
Core Differences in Focus and Techniques
Commutative algebra primarily studies the algebraic structures such as commutative rings, ideals, and modules using techniques like ring theory, homological algebra, and localization, emphasizing purely algebraic properties. Algebraic geometry focuses on the geometric interpretation of solutions to polynomial equations, employing tools from topology, sheaf theory, and scheme theory to analyze varieties and morphisms. The core difference lies in commutative algebra's abstract algebraic approach versus algebraic geometry's blend of algebraic and geometric methods to understand spatial structures.
How Commutative Algebra Informs Algebraic Geometry
Commutative algebra provides the foundational language and tools for algebraic geometry by studying commutative rings, ideals, and modules that correspond to algebraic varieties and schemes. Key concepts like localization, prime ideals, and integral extensions enable the rigorous formulation of geometric properties, such as dimension, smoothness, and singularities within algebraic geometry. The spectrum of a ring, constructed using prime ideals, directly connects commutative algebra structures to the topological and geometric objects studied in algebraic geometry.
Key Theorems Bridging the Two Disciplines
Key theorems bridging commutative algebra and algebraic geometry include Hilbert's Nullstellensatz, which establishes a correspondence between radical ideals in polynomial rings and algebraic sets, forming the foundation for interpreting algebraic varieties via ideal theory. The Krull Dimension Theorem connects the dimension of a ring in commutative algebra with the geometric dimension of algebraic varieties, providing a critical link between algebraic and geometric structures. Serre's criterion for normality and the use of sheaf cohomology further integrate local properties of rings with global geometric features, enhancing the interplay between the two disciplines.
Applications in Mathematics and Beyond
Commutative algebra provides foundational tools for algebraic geometry by studying rings and ideals that describe geometrical spaces algebraically, enabling solutions to polynomial equations. Algebraic geometry applies these concepts to understand geometric shapes, complex curves, and surfaces with profound implications in number theory, cryptography, and error-correcting codes. Together, these fields drive advancements in computational mathematics, coding theory, and mathematical physics, demonstrating broad interdisciplinary applications.
Modern Research Trends and Open Problems
Modern research trends in commutative algebra emphasize homological conjectures, tight closure theory, and the study of singularities through methods like Frobenius splitting and local cohomology, driving the resolution of long-standing problems such as the Direct Summand Conjecture. Algebraic geometry has evolved by integrating derived categories, moduli spaces, and mirror symmetry, with open problems centering on the understanding of Calabi-Yau varieties, minimal model programs, and the birational geometry of higher-dimensional algebraic varieties. The interplay between these fields fosters advances in syzygies, resolution of singularities, and the theory of motives, underpinning significant progress in both abstract theory and practical computation.
Notable Mathematicians and Influential Works
Commutative algebra's foundations were profoundly shaped by Emmy Noether, whose Noetherian rings concept revolutionized the field, while Oscar Zariski and Wolfgang Krull contributed critical insights into ideal theory and valuation theory. Algebraic geometry was deeply influenced by Alexander Grothendieck, whose schemes concept unified geometry and commutative algebra, alongside Jean-Pierre Serre, who advanced coherent sheaves and sheaf cohomology techniques. Their seminal works, such as Grothendieck's "Elements de geometrie algebrique" and Noether's theorem papers, remain cornerstones defining the interplay between these disciplines.
Future Directions and Interdisciplinary Connections
Commutative algebra underpins the algebraic structures essential for advancing algebraic geometry, particularly in resolving singularities and developing computational tools for scheme theory. Future directions involve leveraging homological methods and derived categories to deepen the understanding of moduli spaces and algebraic stacks. Interdisciplinary connections emerge prominently in number theory, cryptography, and mathematical physics, where the algebraic foundations facilitate breakthroughs in understanding space-time structures and coding theory.
Commutative algebra Infographic
 libterm.com
libterm.com