A simply connected space is a topological space without holes, meaning any loop within it can be continuously contracted to a point. This property is vital in fields such as complex analysis, algebraic topology, and physics. Explore the rest of the article to understand how simply connected spaces influence your studies and applications.
Table of Comparison
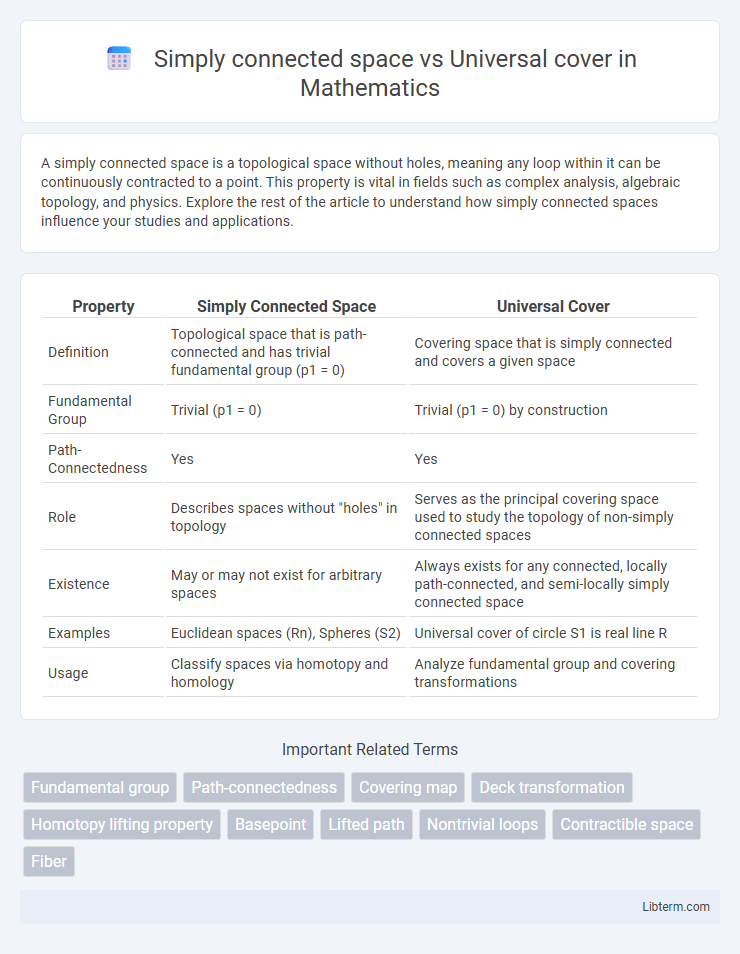
| Property | Simply Connected Space | Universal Cover |
|---|---|---|
| Definition | Topological space that is path-connected and has trivial fundamental group (p1 = 0) | Covering space that is simply connected and covers a given space |
| Fundamental Group | Trivial (p1 = 0) | Trivial (p1 = 0) by construction |
| Path-Connectedness | Yes | Yes |
| Role | Describes spaces without "holes" in topology | Serves as the principal covering space used to study the topology of non-simply connected spaces |
| Existence | May or may not exist for arbitrary spaces | Always exists for any connected, locally path-connected, and semi-locally simply connected space |
| Examples | Euclidean spaces (Rn), Spheres (S2) | Universal cover of circle S1 is real line R |
| Usage | Classify spaces via homotopy and homology | Analyze fundamental group and covering transformations |
Introduction to Simply Connected Spaces
A simply connected space is a topological space that is both path-connected and has a trivial fundamental group, meaning every loop can be continuously contracted to a point. In contrast, the universal cover of a space is a simply connected covering space that maps onto the original space via a continuous surjection. Understanding simply connected spaces is essential for grasping the role of universal covers in algebraic topology, as they provide a canonical example of spaces with trivial fundamental groups.
Definition and Key Properties of Simply Connected Spaces
A simply connected space is a topological space that is path-connected and has a trivial fundamental group, meaning every loop can be continuously contracted to a single point. This property implies the absence of "holes" or "obstructions" in the space, making it an essential concept in algebraic topology. The universal cover of any connected space is always simply connected, serving as a covering space that unwraps all loops to create a space with no nontrivial loops.
Universal Cover: Concept and Importance
The universal cover of a topological space is a simply connected space that maps onto the original space via a continuous surjective covering map, preserving local structure. It plays a crucial role in algebraic topology by enabling the study of fundamental groups through lifting properties and simplifying problems involving loops and paths. Universal covers facilitate the classification of covering spaces and provide insights into the space's global topology by revealing its universal, simply connected counterpart.
Relationship Between Simply Connected Spaces and Universal Covers
A simply connected space is characterized by having no nontrivial loops, meaning every loop can be continuously contracted to a point. The universal cover of a topological space is a simply connected space that covers the original space in a way that locally resembles the original structure. This relationship ensures that the fundamental group of the original space corresponds to the group of deck transformations of its universal cover, establishing a one-to-one correspondence between covering spaces and subgroups of the fundamental group.
Construction of Universal Covers
The construction of universal covers involves creating a simply connected space that maps onto a given topological space via a covering map. This process uses the fundamental group to systematically "unfold" loops in the base space, eliminating holes and ensuring the universal cover is simply connected. The universal cover serves as a principal tool in algebraic topology for studying spaces through their simply connected counterparts.
Examples of Simply Connected Spaces
The 2-dimensional sphere \(S^2\) and the Euclidean space \(\mathbb{R}^n\) are classic examples of simply connected spaces, characterized by their path-connectedness and trivial fundamental group. In contrast, the universal cover of a space like the circle \(S^1\) is the real line \(\mathbb{R}\), which is simply connected and serves to "unwrap" loops in \(S^1\). Simply connected spaces have no non-contractible loops, making them the universal covers of spaces with non-trivial fundamental groups.
Examples of Universal Cover Spaces
The universal cover of a space like the circle S1 is the real line R, which is simply connected and covers S1 via the exponential map. For a torus T2 = S1 x S1, the universal cover is the Euclidean plane R2, providing a simply connected covering space that unwraps the torus's loops. Complex projective spaces CPn have universal covers that are often more intricate, but for example, the universal cover of the real projective plane RP2 is the 2-sphere S2, which is simply connected and covers RP2 via a double covering map.
Topological Implications and Applications
Simply connected spaces are topological spaces without nontrivial loops, meaning every loop can be continuously contracted to a point, which implies a trivial fundamental group. The universal cover of a topological space serves as a simply connected covering space that maps onto the original space, revealing the structure of its fundamental group through covering transformations. Applications in algebraic topology include classification of covering spaces, analysis of fiber bundles, and solving complex problems in homotopy theory by lifting paths and homotopies to the universal covering space.
Common Misconceptions and Differences
A simply connected space is a topological space with no nontrivial loops, meaning every loop can be continuously contracted to a point, while a universal cover is a covering space that is simply connected and maps onto a given space. A common misconception is that simply connected spaces and universal covers are interchangeable; however, the universal cover depends on the base space and serves as a tool to study its topological properties. The universal cover is unique up to homeomorphism and provides a way to analyze complex spaces through their simpler, simply connected counterparts, but not all simply connected spaces arise as universal covers.
Conclusion: Choosing Between Simply Connected Spaces and Universal Covers
Simply connected spaces exhibit no nontrivial loops, making them ideal for simplifying topological analysis and ensuring uniqueness in path lifting. Universal covers serve as a powerful tool to study spaces with complex fundamental groups by providing a simply connected covering space that unravels these complexities. Selecting between working directly with a simply connected space or its universal cover hinges on the problem's need for topological simplicity versus the benefits of relating to the original space's structure through the covering map.
Simply connected space Infographic
 libterm.com
libterm.com