A torsion module is an important concept in algebra where every element is annihilated by some nonzero element of the ring, meaning it has finite order relative to the ring's multiplication. This property plays a crucial role in understanding the structure of modules over rings, notably in algebraic number theory and homological algebra. Explore the rest of the article to deepen your understanding of torsion modules and their applications.
Table of Comparison
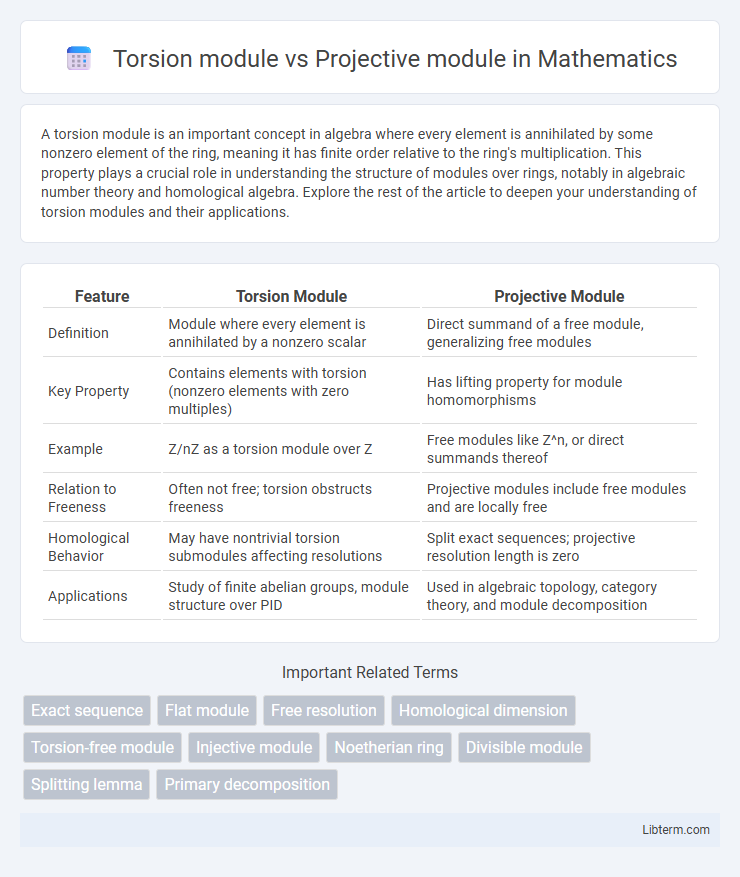
| Feature | Torsion Module | Projective Module |
|---|---|---|
| Definition | Module where every element is annihilated by a nonzero scalar | Direct summand of a free module, generalizing free modules |
| Key Property | Contains elements with torsion (nonzero elements with zero multiples) | Has lifting property for module homomorphisms |
| Example | Z/nZ as a torsion module over Z | Free modules like Z^n, or direct summands thereof |
| Relation to Freeness | Often not free; torsion obstructs freeness | Projective modules include free modules and are locally free |
| Homological Behavior | May have nontrivial torsion submodules affecting resolutions | Split exact sequences; projective resolution length is zero |
| Applications | Study of finite abelian groups, module structure over PID | Used in algebraic topology, category theory, and module decomposition |
Introduction to Module Theory
Torsion modules consist of elements annihilated by some nonzero scalar of the ring, highlighting the presence of zero divisors within the module structure. Projective modules serve as direct summands of free modules, characterized by their lifting property that facilitates splitting exact sequences and ensuring module decomposability. In module theory, understanding the distinction between torsion and projective modules is essential for analyzing module behavior over different rings, especially in the context of homological algebra and ring theory.
Defining Torsion Modules
A torsion module over a commutative ring R is a module M where every element m in M is annihilated by some nonzero element r in R, meaning rm = 0 for some r 0. This property distinguishes torsion modules from projective modules, which are direct summands of free modules and lack such annihilation behavior. Torsion modules often arise in the study of modules over integral domains, highlighting elements with finite order under scalar multiplication, unlike projective modules characterized by their lifting and splitting properties.
Understanding Projective Modules
Projective modules are direct summands of free modules, characterized by their lifting property which allows every surjective module homomorphism to be lifted across them. Unlike torsion modules, which consist of elements annihilated by nonzero scalars and thus exhibit torsion behavior, projective modules maintain a torsion-free structure when defined over integral domains. Understanding projective modules involves recognizing their role in splitting exact sequences and ensuring that related homological dimensions, like projective dimension, are minimized, which is vital for decomposing modules and studying module categories.
Key Differences Between Torsion and Projective Modules
Torsion modules consist of elements annihilated by nonzero elements of the ring, whereas projective modules are direct summands of free modules, characterized by their lifting property. Torsion modules commonly arise over integral domains with nontrivial zero divisors, reflecting elements with finite order, while projective modules maintain structural decomposability and exhibit homological projectivity. The key difference lies in torsion's dependence on element annihilation versus projective modules' intrinsic splitting and exact sequence lifting properties in module theory.
Examples of Torsion Modules
Torsion modules over a ring R include examples such as the abelian group Z/nZ, where every element has finite order, making it a classic torsion module over Z. Another example is the module Q/Z, consisting of rational numbers modulo integers, which is torsion since every element has finite order. In contrast, projective modules like free modules or direct summands of free modules do not contain torsion elements, highlighting the structural difference between torsion and projective modules.
Examples of Projective Modules
Projective modules include free modules like \( R^n \) over a ring \( R \), which provide canonical examples due to their direct summand property. Another key example is the module \( \mathbb{Z} \) over itself, which is projective but not torsion, contrasting with torsion modules such as \( \mathbb{Z}/n\mathbb{Z} \). Finitely generated projective modules over a commutative ring often appear as direct summands of free modules, highlighting their structural distinction from torsion modules.
Structural Properties: Torsion vs Projective
Torsion modules are characterized by elements annihilated by nonzero scalars, reflecting the presence of torsion submodules and lack of free structure. Projective modules exhibit a direct summand structure of free modules, ensuring liftings of homomorphisms and preserving exact sequences. The structural contrast centers on torsion modules often failing to be projective due to torsion elements, while projective modules possess torsion-free, well-behaved decompositions facilitating module extensions.
Applications in Algebra: Torsion and Projective Modules
Torsion modules are essential in classifying elements annihilated by nonzero scalars, playing a crucial role in module decomposition over integral domains and facilitating the study of divisibility properties. Projective modules, characterized by their lifting property and direct summand status in free modules, are fundamental in resolving modules and constructing exact sequences in homological algebra. Applications in algebra include using torsion modules to analyze algebraic structures such as abelian groups and modules over principal ideal domains, while projective modules underpin the classification of vector bundles and simplify complex module manipulations in ring theory.
Homological Perspectives: Extensions and Resolutions
Torsion modules often exhibit non-trivial Ext groups with projective modules, reflecting their failure to be projective and indicating the presence of higher homological complexity in extensions. Projective modules, characterized by vanishing Ext^1 with any module, serve as building blocks in projective resolutions, enabling simplified computations in homological algebra. The contrast between torsion and projective modules is pivotal in understanding the structure of modules over a ring, as torsion modules typically require longer or more intricate projective resolutions due to their extension behavior.
Summary and Comparative Insights
Torsion modules consist of elements annihilated by nonzero ring elements, highlighting constraints within module structure over domains like integral domains. Projective modules, characterized by their lifting property and direct summand relationship to free modules, demonstrate a form of structural flexibility absent in torsion modules. Comparative insights reveal that torsion modules often represent "dependence" or "obstruction" phenomena in module theory, whereas projective modules provide tools for decomposition and homological algebra applications, making them crucial in areas like algebraic topology and category theory.
Torsion module Infographic
 libterm.com
libterm.com