Trajectory refers to the path that an object follows as it moves through space, influenced by forces such as gravity, velocity, and acceleration. Understanding trajectory is crucial in fields ranging from physics and engineering to sports and space exploration. Explore the rest of the article to discover how trajectory impacts various real-world applications and your everyday life.
Table of Comparison
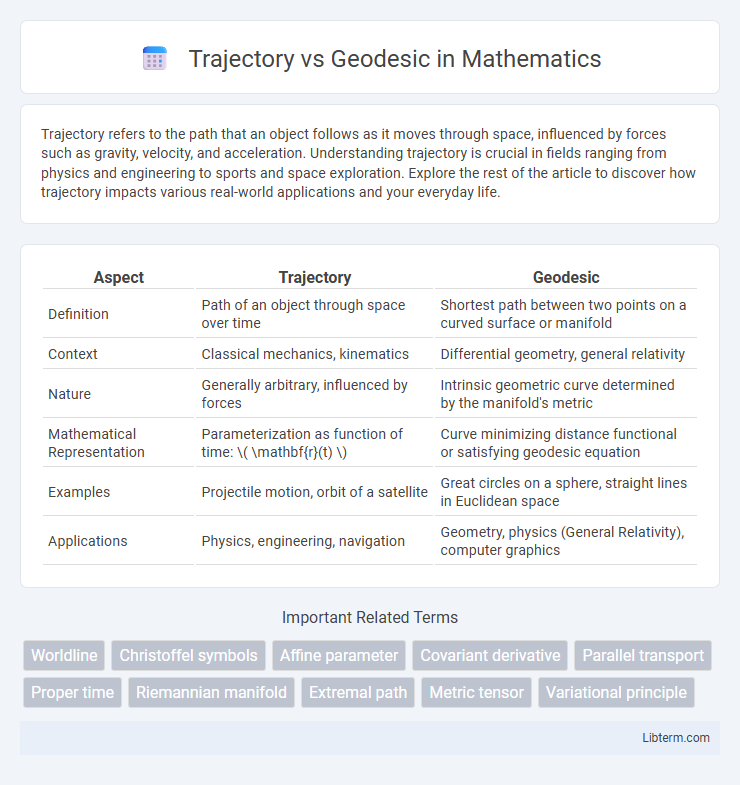
| Aspect | Trajectory | Geodesic |
|---|---|---|
| Definition | Path of an object through space over time | Shortest path between two points on a curved surface or manifold |
| Context | Classical mechanics, kinematics | Differential geometry, general relativity |
| Nature | Generally arbitrary, influenced by forces | Intrinsic geometric curve determined by the manifold's metric |
| Mathematical Representation | Parameterization as function of time: \( \mathbf{r}(t) \) | Curve minimizing distance functional or satisfying geodesic equation |
| Examples | Projectile motion, orbit of a satellite | Great circles on a sphere, straight lines in Euclidean space |
| Applications | Physics, engineering, navigation | Geometry, physics (General Relativity), computer graphics |
Introduction to Trajectory and Geodesic
A trajectory represents the path that an object follows through space as a function of time, often influenced by external forces and initial conditions. A geodesic, in contrast, is the shortest path between two points on a curved surface or manifold, determined solely by the geometry of the space without external influence. Understanding the differences between trajectories and geodesics is fundamental in fields such as physics, robotics, and differential geometry.
Defining Trajectory: Path of Motion
A trajectory represents the specific path that an object follows as it moves through space over time, determined by its velocity and external forces. Unlike a geodesic, which is the shortest path between two points on a curved surface, a trajectory can be influenced by factors such as gravity, friction, and propulsion. In physics and engineering, analyzing the trajectory is crucial for predicting the future position and behavior of moving bodies in various environments.
Understanding Geodesic: Shortest Path Concept
A geodesic represents the shortest path between two points on a curved surface or manifold, generalizing the concept of a straight line in Euclidean space. Unlike arbitrary trajectories, geodesics minimize distance based on the intrinsic geometry of the surface, making them critical in fields like differential geometry, general relativity, and navigation. Calculating geodesics involves solving the geodesic equation derived from the surface's metric tensor, ensuring the path accounts for curvature and anisotropy in the underlying space.
Key Differences Between Trajectory and Geodesic
Trajectory refers to the path a moving object follows through space as a function of time, often influenced by forces like gravity or propulsion, while a geodesic is the shortest path between two points on a curved surface or manifold, determined by the intrinsic geometry. Trajectories depend on external factors and dynamic conditions, whereas geodesics are purely geometric constructs independent of time or forces. In differential geometry and physics, geodesics represent idealized paths minimizing distance or action, contrasting with the variable and force-driven nature of trajectories.
Mathematical Formulation of Trajectories
Trajectories in mathematics describe the path traced by a moving point in a given space and are typically represented by parametric equations or functions of time, such as \( \mathbf{r}(t) = (x(t), y(t), z(t)) \). The mathematical formulation involves differential equations that define velocity and acceleration vectors, enabling the characterization of motion dynamics along the curve. Unlike geodesics, which minimize distance within a curved space and are solutions to the geodesic equation derived from the metric tensor, trajectories can follow arbitrary paths influenced by forces and constraints.
Geodesics in Geometry and Physics
Geodesics represent the shortest path between two points on a curved surface or manifold, fundamental in differential geometry and general relativity. In physics, geodesics describe the natural motion of particles under no external forces, tracing paths determined by the spacetime curvature induced by mass and energy. The mathematical formulation involves solving the geodesic equation derived from the metric tensor, revealing intrinsic properties of space and time in Einstein's theory of gravity.
Trajectories in Classical and Modern Physics
Trajectories in classical physics describe the paths of particles under forces, typically represented by solutions to Newton's equations of motion in Euclidean space. In modern physics, trajectories are generalized through geodesics, which represent the shortest paths in curved spacetime governed by general relativity, reflecting gravitational effects on particles and light. The transition from trajectory concepts to geodesics encapsulates the shift from force-based dynamics to geometric interpretations of motion.
Geodesic Applications in General Relativity
Geodesics represent the shortest paths between points on curved spacetime, serving as the natural trajectories of free-falling particles in General Relativity. These curves are critical in predicting planetary orbits, light bending near massive objects, and the propagation of gravitational waves. Understanding geodesic motion allows physicists to analyze how matter and radiation move under the influence of gravity described by Einstein's field equations.
Real-world Examples: Trajectory vs Geodesic
In urban navigation, a trajectory represents the actual path taken by a vehicle, often influenced by road networks and traffic conditions, whereas a geodesic is the shortest distance between two points on Earth's curved surface, typically used in flight planning. For instance, aircraft pilots follow geodesic routes called great circles to minimize travel time and fuel consumption, while drivers follow trajectories defined by highways and street layouts. In robotics, trajectory planning involves creating feasible and collision-free paths within a given environment, contrasting with the geodesic path which serves as an ideal reference for shortest distance on a manifold or terrain.
Summary and Practical Implications
Trajectories represent the actual paths taken by objects moving through space and time, while geodesics define the shortest or extremal paths between points in curved spacetime, essential in General Relativity. Understanding the distinction guides navigation systems, astrophysical modeling, and drone flight optimization by predicting real motion versus idealized paths under gravitational influence. Practical applications rely on accurate trajectory calculation for collision avoidance, whereas geodesics provide theoretical baselines for efficient routing and spacetime curvature analysis.
Trajectory Infographic
 libterm.com
libterm.com