A quasimetric is a distance function that relaxes symmetry, meaning d(x, y) may not equal d(y, x), unlike a traditional metric. This property makes quasimetrics essential for modeling asymmetric relationships in networks, optimization problems, and various applied mathematics fields. Discover how understanding quasimetrics can improve your grasp of complex distance structures by reading the full article.
Table of Comparison
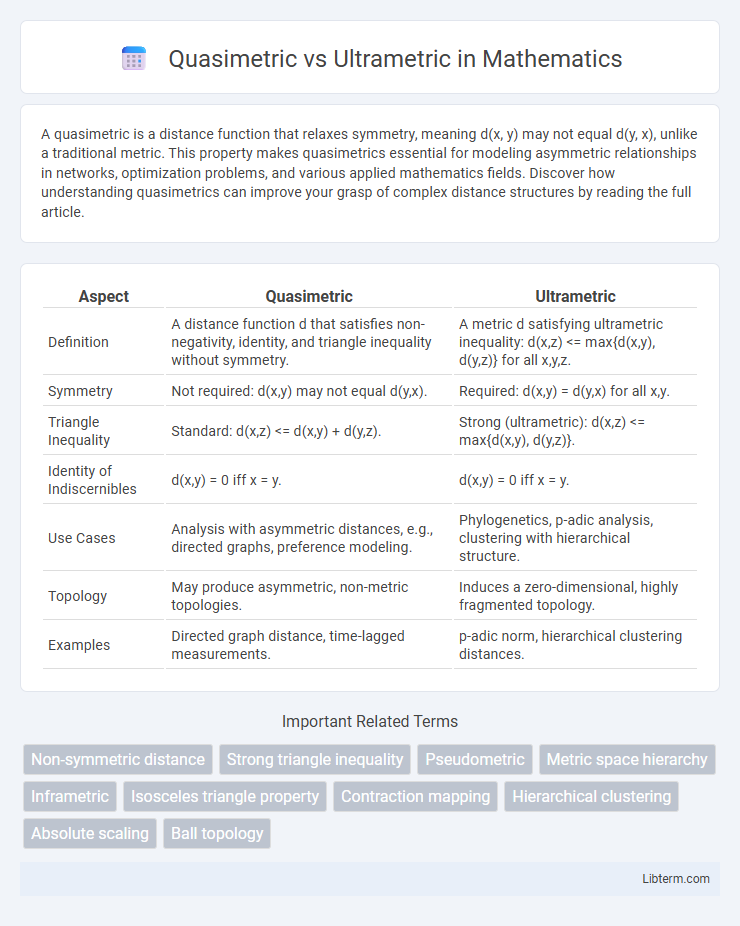
| Aspect | Quasimetric | Ultrametric |
|---|---|---|
| Definition | A distance function d that satisfies non-negativity, identity, and triangle inequality without symmetry. | A metric d satisfying ultrametric inequality: d(x,z) <= max{d(x,y), d(y,z)} for all x,y,z. |
| Symmetry | Not required: d(x,y) may not equal d(y,x). | Required: d(x,y) = d(y,x) for all x,y. |
| Triangle Inequality | Standard: d(x,z) <= d(x,y) + d(y,z). | Strong (ultrametric): d(x,z) <= max{d(x,y), d(y,z)}. |
| Identity of Indiscernibles | d(x,y) = 0 iff x = y. | d(x,y) = 0 iff x = y. |
| Use Cases | Analysis with asymmetric distances, e.g., directed graphs, preference modeling. | Phylogenetics, p-adic analysis, clustering with hierarchical structure. |
| Topology | May produce asymmetric, non-metric topologies. | Induces a zero-dimensional, highly fragmented topology. |
| Examples | Directed graph distance, time-lagged measurements. | p-adic norm, hierarchical clustering distances. |
Introduction to Quasimetric and Ultrametric Spaces
Quasimetric spaces generalize metric spaces by relaxing the symmetry condition, allowing distance from point A to B to differ from distance B to A, which models asymmetric relationships in data. Ultrametric spaces impose a strong form of the triangle inequality, where the distance between two points is at most the maximum of the distances to a third point, crucial for hierarchical clustering and p-adic analysis. These distinct structures enable specialized applications in fields such as computer science, biology, and number theory, leveraging their unique distance properties.
Defining Quasimetrics: Key Properties
Quasimetric spaces generalize metric spaces by relaxing the symmetry requirement, meaning the distance from point A to B may differ from B to A. Key properties include non-negativity, identity of indiscernibles (distance zero implies identical points), and the triangle inequality, which must hold without symmetry. These features distinguish quasimetrics from ultrametrics, where the strong triangle inequality and symmetry strictly apply.
Understanding Ultrametrics: Features and Axioms
Ultrametrics are specialized distance functions in metric spaces where the strong triangle inequality d(x,z) <= max{d(x,y), d(y,z)} holds for all points x, y, z, distinguishing them from quasimetric spaces that relax symmetry or triangle inequality conditions. Ultrametric spaces exhibit hierarchical clustering properties, meaning any triplet of points forms an isosceles or equilateral triangle with the base no longer than the legs, fundamentally supporting tree-like data structures in fields like phylogenetics and p-adic analysis. Key axioms of ultrametrics include non-negativity, identity of indiscernibles, symmetry, and the ultrametric inequality, making them essential in modeling datasets with strong inherent cluster formations.
Major Differences Between Quasimetric and Ultrametric
Quasimetric and ultrametric are both distance functions, but quasimetric only satisfies non-negativity and the triangle inequality without requiring symmetry, while ultrametric is a stronger form of metric that fulfills the ultrametric inequality d(x,z) <= max{d(x,y), d(y,z)} and is symmetric. The major difference lies in the relaxation of symmetry in quasimetric spaces, allowing d(x,y) d(y,x), whereas ultrametric spaces always have symmetrical distance measures reflecting hierarchical clustering properties. Ultrametrics are commonly applied in phylogenetics and p-adic number theory, while quasimetrics appear in asymmetric contexts such as directed graphs and time-dependent processes.
Topological Implications in Quasimetric vs Ultrametric
Quasimetrics relax the symmetry condition found in ultrametrics, allowing d(x, y) d(y, x), which leads to richer but more complex topological structures lacking the strong hierarchical clustering characteristic of ultrametric spaces. Ultrametrics satisfy the strong triangle inequality d(x, z) <= max{d(x, y), d(y, z)}, ensuring that balls are either nested or disjoint and inducing a tree-like topology facilitating applications in phylogenetics and data analysis. The topological implications reveal that ultrametric spaces are zero-dimensional, totally disconnected, and often serve as ideal models for hierarchical data, while quasimetric spaces support asymmetric relations common in directed graphs and computational geometry with more intricate convergence properties.
Examples of Quasimetric Spaces
Quasimetric spaces generalize metric spaces by relaxing the symmetry condition, allowing the distance from point A to B to differ from B to A, while ultrametric spaces enforce a strong triangle inequality where the distance between any two points is at most the maximum of the distances via a third point. Examples of quasimetric spaces include directed graph shortest path distances, where the cost to travel from vertex A to B may differ from B to A, and time-dependent travel times in transportation networks that vary based on direction. These examples illustrate how quasimetric structures capture asymmetric distance relations not present in ultrametric or standard metric spaces.
Real-World Applications of Ultrametrics
Ultrametric spaces are extensively used in hierarchical clustering across bioinformatics and linguistics, where the strong triangle inequality reflects natural tree-like structures in data, such as evolutionary relationships or language taxonomy. Quasimetric spaces, lacking symmetry but preserving a relaxed triangle inequality, appear in computer science applications like network latency modeling and routing, where asymmetry captures directional cost or time differences. The ultrametric property enables efficient algorithms for phylogenetic tree reconstruction and p-adic number analysis in computational number theory, making them indispensable in modeling nested hierarchical systems.
Advantages and Limitations of Quasimetrics
Quasimetrics offer greater flexibility than ultrametrics by relaxing the strong triangle inequality, allowing asymmetric distance measurement useful in directed graphs, machine learning, and preference modeling. This flexibility enables more accurate representation of real-world scenarios where symmetry or strict hierarchical clustering is not present. However, quasimetrics may complicate analysis and algorithms due to their weaker structural constraints compared to ultrametrics, which guarantee well-defined hierarchical clustering and simplify computational processes.
When to Use Quasimetric or Ultrametric Analysis
Quasimetric analysis is suitable for datasets where asymmetric relationships or directional distances are present, such as in transportation networks or preference rankings, as it relaxes the symmetry requirement of distances. Ultrametric analysis excels in hierarchical clustering and phylogenetics, where the strong triangle inequality models nested structures and evolutionary relationships effectively. Choose quasimetric models when capturing non-symmetric, possibly incomplete data is crucial, while ultrametrics fit well for inherently hierarchical or tree-like data structures demanding strict ultrametric conditions.
Future Directions in Metric Space Research
Future directions in metric space research emphasize developing generalized distance functions beyond quasimetric and ultrametric frameworks to better model asymmetric relations and hierarchical structures in complex data. Innovations in embedding techniques and topological data analysis aim to unify quasimetric spaces with ultrametric constraints, enhancing applications in machine learning and network science. Advances also focus on computational efficiency and robustness in high-dimensional spaces, driving novel algorithms for clustering and similarity search.
Quasimetric Infographic
 libterm.com
libterm.com