The direct product is a fundamental concept in mathematics, particularly in group theory and linear algebra, enabling the combination of two algebraic structures into a single, more complex entity while preserving their individual properties. Understanding how direct products function can help you analyze and simplify problems involving multiple components or systems. Explore the rest of the article to discover detailed examples and applications of direct products in various mathematical contexts.
Table of Comparison
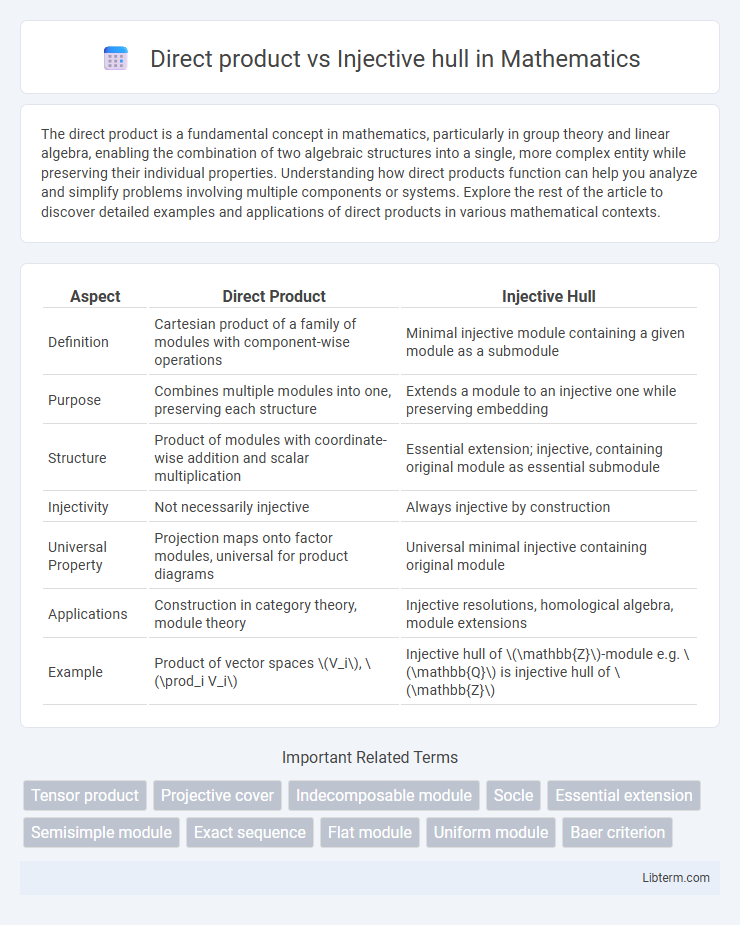
| Aspect | Direct Product | Injective Hull |
|---|---|---|
| Definition | Cartesian product of a family of modules with component-wise operations | Minimal injective module containing a given module as a submodule |
| Purpose | Combines multiple modules into one, preserving each structure | Extends a module to an injective one while preserving embedding |
| Structure | Product of modules with coordinate-wise addition and scalar multiplication | Essential extension; injective, containing original module as essential submodule |
| Injectivity | Not necessarily injective | Always injective by construction |
| Universal Property | Projection maps onto factor modules, universal for product diagrams | Universal minimal injective containing original module |
| Applications | Construction in category theory, module theory | Injective resolutions, homological algebra, module extensions |
| Example | Product of vector spaces \(V_i\), \(\prod_i V_i\) | Injective hull of \(\mathbb{Z}\)-module e.g. \(\mathbb{Q}\) is injective hull of \(\mathbb{Z}\) |
Understanding Direct Products in Module Theory
Direct products in module theory form a module consisting of tuples from given modules, preserving operations componentwise, which contrasts with injective hulls that serve as minimal injective extensions of modules. Understanding direct products involves recognizing their role in constructing large modules from families of modules, where surjective projections facilitate analysis of each component. These structures are essential in module theory for decompositions and studying module homomorphisms, differing fundamentally from injective hulls used for embedding modules into injective ones.
The Concept of the Injective Hull
The injective hull of a module is the smallest injective module containing it as a submodule, providing an essential extension that preserves injectivity properties. This construction is crucial in homological algebra for embedding modules into injective objects, allowing the study of module extensions and resolutions. Unlike the direct product of modules, which aggregates multiple modules without minimality or injectivity constraints, the injective hull uniquely refines a given module within an injective framework.
Key Properties of Direct Products
Direct products in category theory are constructed by combining objects and morphisms componentwise, preserving their individual structures within a unified system. Key properties include the existence of projection morphisms that retrieve each component, the universal mapping property allowing unique morphisms into the product, and the preservation of limits when formed in complete categories. Unlike injective hulls, which extend objects to minimal injective objects, direct products focus on assembling multiple objects without necessarily enhancing injectivity or minimality.
Essential Properties of Injective Hulls
Injective hulls are minimal essential extensions of modules that are injective, ensuring every element of the module is embedded in an injective module without redundancy. Unlike direct products, which combine multiple modules possibly increasing complexity and redundancy, injective hulls preserve essentiality and minimality of embeddings, making them crucial in homological algebra. Their unique property of being the smallest injective module containing a given module guarantees maximal efficiency in extending homological properties.
Comparison: Direct Product vs Injective Hull
The direct product combines multiple modules into a single product module, preserving component-wise operations and often resulting in a larger, more complex structure, whereas the injective hull is a minimal injective module containing a given module as an essential submodule, focusing on injectivity and extension properties. Direct products maintain the internal structure of the module family without necessarily enhancing injectivity, while injective hulls serve as minimal injective envelopes ensuring essential extensions and maximal injectivity. The key distinction lies in their categorical roles: direct products act as limits preserving product universality, and injective hulls are minimal injective objects facilitating exact extension and embedding.
Structural Differences in Module Decomposition
Direct product of modules constructs a new module from a family by element-wise multiplication, preserving component integration but often lacks minimality in decomposition. Injective hull represents the smallest injective module containing a given module, providing an essential extension that respects indecomposability and minimality in decomposition. Structurally, direct products emphasize component aggregation while injective hulls ensure maximal extension and structural refinement through essential embeddings.
Applications of Direct Products in Algebra
Direct products serve as a fundamental tool in algebra for constructing new algebraic structures, such as groups, rings, and modules, by combining multiple components while preserving their individual operations. They enable the study of complex systems through the behavior of their factors, facilitating decompositions and classifications in group theory and module theory. Injective hulls, in contrast, provide minimal injective extensions important for addressing exactness properties and embedding problems but do not offer the constructive versatility found in direct products for building composite algebraic objects.
Uses of Injective Hulls in Module Theory
Injective hulls serve as essential tools in module theory for embedding modules into minimal injective modules, enabling clearer analysis of module structure and homological properties. They facilitate the construction of minimal injective resolutions, which are pivotal for computing derived functors such as Ext and Tor. Unlike direct products that assemble modules without guaranteeing injectivity or minimality, injective hulls ensure maximal essential extensions that preserve module characteristics crucial for decomposition and classification tasks.
Examples Illustrating Direct Product and Injective Hull
The direct product of modules, such as \(\mathbb{Z}/2\mathbb{Z} \times \mathbb{Z}/3\mathbb{Z}\), combines multiple structures into a single object with component-wise operations, illustrating how elements behave independently. An injective hull example includes embedding the module \(\mathbb{Z}/n\mathbb{Z}\) into the divisible group \(\mathbb{Q}/\mathbb{Z}\), which serves as its minimal injective extension by preserving homomorphic properties. These examples highlight the contrast where direct products aggregate modules, while injective hulls extend modules minimally to injective ones.
Choosing Between Direct Product and Injective Hull in Practice
Choosing between direct product and injective hull depends on the algebraic context and desired properties; direct products preserve component-wise structure and are useful for constructing large, explicit modules, while injective hulls provide minimal essential extensions ensuring injectivity. In practice, injective hulls are preferred for simplifying homological computations due to their minimality and injective nature, whereas direct products offer versatility in representing complex objects without guaranteeing injective characteristics. Understanding these distinctions guides algebraists in module theory and homological algebra applications where injectivity and structural control are critical.
Direct product Infographic
 libterm.com
libterm.com