Commutative algebra focuses on the study of commutative rings, their ideals, and modules, forming the algebraic foundation for algebraic geometry and number theory. Understanding the properties of ring structures and their homomorphisms provides crucial insights into solving polynomial equations and exploring algebraic varieties. Discover how these concepts can deepen your mathematical knowledge by reading the rest of the article.
Table of Comparison
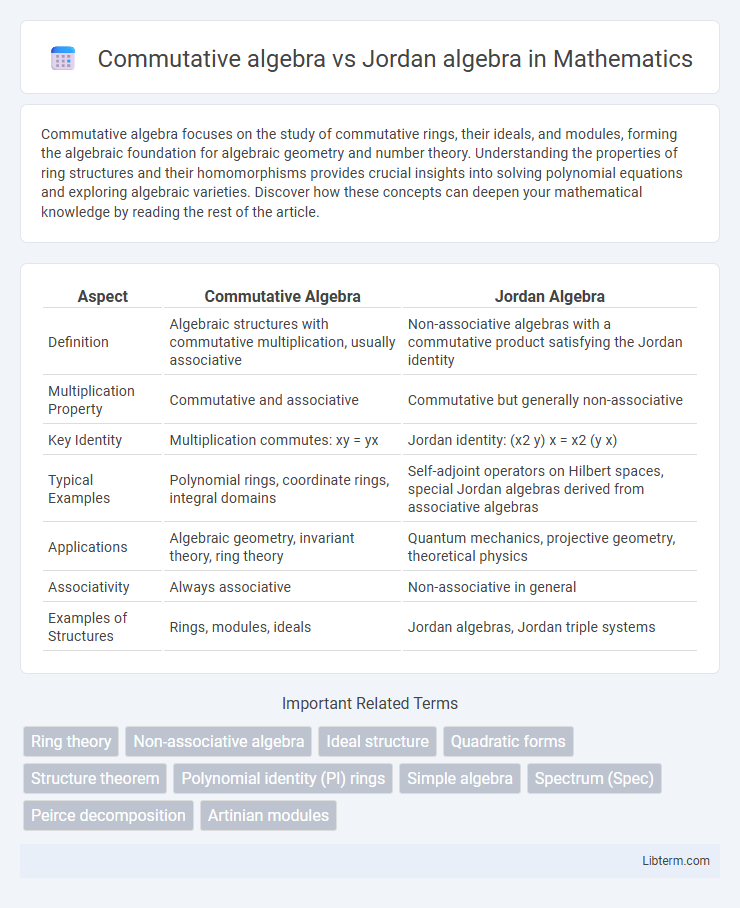
| Aspect | Commutative Algebra | Jordan Algebra |
|---|---|---|
| Definition | Algebraic structures with commutative multiplication, usually associative | Non-associative algebras with a commutative product satisfying the Jordan identity |
| Multiplication Property | Commutative and associative | Commutative but generally non-associative |
| Key Identity | Multiplication commutes: xy = yx | Jordan identity: (x2 y) x = x2 (y x) |
| Typical Examples | Polynomial rings, coordinate rings, integral domains | Self-adjoint operators on Hilbert spaces, special Jordan algebras derived from associative algebras |
| Applications | Algebraic geometry, invariant theory, ring theory | Quantum mechanics, projective geometry, theoretical physics |
| Associativity | Always associative | Non-associative in general |
| Examples of Structures | Rings, modules, ideals | Jordan algebras, Jordan triple systems |
Definition of Commutative Algebra
Commutative algebra is a branch of algebra focusing on commutative rings where the multiplication operation is commutative, meaning for any elements a and b, the equation ab = ba holds. This area studies structures such as polynomial rings, integral domains, and algebraic varieties fundamental to algebraic geometry and number theory. In contrast, Jordan algebra is a non-associative algebra mainly used in quantum mechanics, defined by the Jordan product satisfying commutativity and the Jordan identity, differentiating it from classical commutative algebra.
Definition of Jordan Algebra
Jordan algebra is a non-associative algebra defined by the commutative product \( a \circ b = \frac{1}{2}(ab + ba) \) and satisfies the Jordan identity \((a \circ b) \circ (a \circ a) = a \circ (b \circ (a \circ a))\). Unlike commutative algebra, which requires associative multiplication for its elements, Jordan algebras generalize commutative algebras by relaxing associativity while preserving a symmetric product and specific polynomial identities. These structures arise notably in quantum mechanics and projective geometry, contrasting with the typically associative operations in commutative algebra.
Historical Development and Origins
Commutative algebra originated in the 19th century as a foundational framework for algebraic geometry and number theory, focusing on commutative rings and their ideals. Jordan algebra emerged in the 1930s from the work of Pascual Jordan, inspired by quantum mechanics to generalize associative algebras with a symmetrized product. While commutative algebra traces its roots to classical polynomial ring theory, Jordan algebra represents a novel non-associative algebraic structure influenced by physics and operator theory.
Core Structures and Operations
Commutative algebra centers on commutative rings where multiplication satisfies the commutative property, playing a fundamental role in algebraic geometry and number theory. Jordan algebras, defined by a symmetrized product \( a \circ b = \frac{1}{2}(ab + ba) \), emphasize non-associative structures relevant to quantum mechanics and projective geometry. The core operations in commutative algebra involve ideals and ring homomorphisms, whereas Jordan algebras focus on idempotents and the Jordan identity, distinguishing their algebraic frameworks.
Key Differences in Algebraic Properties
Commutative algebra is centered on rings where the multiplication operation is commutative, meaning ab = ba for all elements, while Jordan algebra relaxes associativity but maintains commutativity with the Jordan identity (a^2 (b a) = a (a^2 b)). Unlike commutative algebras that emphasize ideals and module theory, Jordan algebras are non-associative and arise primarily in the study of quantum mechanics and projective geometry. The key difference lies in the associative property: commutative algebras are associative, whereas Jordan algebras are generally non-associative but satisfy a weaker form of associativity through the Jordan identity.
Applications in Mathematics and Physics
Commutative algebra underpins algebraic geometry and number theory by studying rings where multiplication is commutative, enabling the analysis of polynomial equations and algebraic varieties essential for cryptography and coding theory. Jordan algebras, characterized by a non-associative multiplication related to observables in quantum mechanics, play a critical role in the mathematical formulation of quantum theory and projective geometry. These algebraic structures serve complementary purposes, with commutative algebra primarily influencing classical algebraic structures and Jordan algebras providing frameworks for quantum physics and symmetric spaces.
Comparison of Representation Theories
Commutative algebra's representation theory primarily deals with modules over commutative rings, focusing on ideals, prime spectra, and localization techniques that enable classification via homological methods. Jordan algebra representation theory centers on nonassociative structures where representations involve linear maps preserving the Jordan product, emphasizing Peirce decompositions and quadratic representations essential for understanding algebraic and geometric symmetries. The contrasting frameworks highlight how commutative algebras use module categories rooted in ring homomorphisms while Jordan algebras require specialized modules reflecting their nonassociative identities and applications in physics and geometry.
Key Theorems and Results
Commutative algebra centers on structures where multiplication is commutative, with key theorems such as Hilbert's Nullstellensatz linking algebraic sets and ideals, and Krull's principal ideal theorem providing dimension bounds for rings. Jordan algebras emphasize nonassociative algebras defined by the Jordan identity, with the Albert Theorem characterizing exceptional simple Jordan algebras and the Koecher-Vinberg theorem connecting Jordan algebras to symmetric cones in analysis. The distinct foundational results in each area illustrate commutative algebra's deep ties to algebraic geometry and ring theory, contrasted with Jordan algebra's role in functional analysis and quantum mechanics.
Examples Illustrating Each Algebra
Commutative algebra includes structures like polynomial rings \( \mathbb{R}[x] \) and rings of continuous functions \( C(X) \), where multiplication is associative and commutative, enabling applications in algebraic geometry and number theory. Jordan algebras, exemplified by the algebra of \( n \times n \) self-adjoint matrices over the reals under the Jordan product \( A \circ B = \frac{1}{2}(AB + BA) \), are non-associative but commutative and play a crucial role in quantum mechanics and projective geometry. These examples highlight how commutative algebras prioritize associativity, while Jordan algebras relax associativity to model symmetric observables in physics.
Future Directions and Open Problems
Future research in commutative algebra emphasizes resolving long-standing conjectures on ring homomorphisms and exploring interactions with computational algebraic geometry. Jordan algebra studies prioritize classification of infinite-dimensional cases and applications to quantum information theory and non-associative geometry. Open problems include understanding the representation theory of Jordan algebras and developing new invariants that connect both algebraic structures for potential breakthroughs in mathematical physics and cryptography.
Commutative algebra Infographic
 libterm.com
libterm.com