Presheaves provide a foundational framework in category theory and algebraic geometry, assigning data to open sets of a topological space in a way that respects restriction maps. They play a critical role in understanding local-to-global principles by encoding how local information on a space can be consistently related across overlapping regions. Explore the rest of this article to deepen your understanding of presheaves and their applications.
Table of Comparison
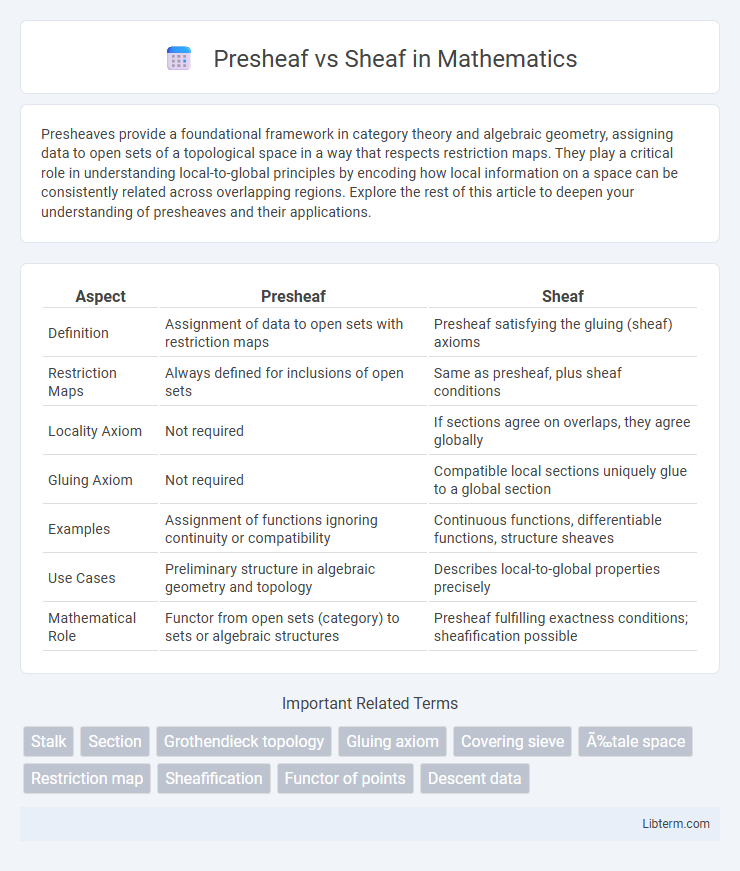
| Aspect | Presheaf | Sheaf |
|---|---|---|
| Definition | Assignment of data to open sets with restriction maps | Presheaf satisfying the gluing (sheaf) axioms |
| Restriction Maps | Always defined for inclusions of open sets | Same as presheaf, plus sheaf conditions |
| Locality Axiom | Not required | If sections agree on overlaps, they agree globally |
| Gluing Axiom | Not required | Compatible local sections uniquely glue to a global section |
| Examples | Assignment of functions ignoring continuity or compatibility | Continuous functions, differentiable functions, structure sheaves |
| Use Cases | Preliminary structure in algebraic geometry and topology | Describes local-to-global properties precisely |
| Mathematical Role | Functor from open sets (category) to sets or algebraic structures | Presheaf fulfilling exactness conditions; sheafification possible |
Introduction to Presheaves and Sheaves
Presheaves assign data to open sets of a topological space, allowing restriction maps between these sets without enforcing compatibility conditions. Sheaves refine presheaves by requiring that local data determined on overlapping open sets uniquely glues together to form global data, ensuring consistency. This distinction is fundamental in topology and algebraic geometry for tracking local-to-global properties.
Key Definitions: Presheaf vs. Sheaf
A presheaf assigns data to open sets of a topological space with restriction maps between these sets, but does not necessarily satisfy the gluing condition. A sheaf is a presheaf that fulfills two additional axioms: locality, where sections that agree on overlaps are identical, and gluing, where compatible local sections can be uniquely combined into a global section. The key distinction lies in the sheaf's ability to ensure consistent and unique reconstruction of global data from local information, unlike a general presheaf.
Core Differences Between Presheaves and Sheaves
Presheaves assign data to open sets of a topological space but lack the condition that local consistency implies global consistency, which is essential for a sheaf. Sheaves require that for any open cover, sections defined locally that agree on overlaps uniquely glue together to form a global section. This gluing condition distinguishes sheaves from presheaves, ensuring coherence and effective localization of data across the space.
Examples Illustrating Presheaf and Sheaf Concepts
A presheaf on a topological space assigns data to each open set without requiring locality or gluing conditions, such as the example of continuous functions defined on open subsets where restriction maps simply limit functions to smaller opens. A sheaf further satisfies the condition that local sections agreeing on overlaps uniquely glue to a global section, exemplified by the sheaf of continuous functions where functions defined on overlapping open sets that agree can be combined into a single continuous function on the union. These examples highlight the key distinction: presheaves allow arbitrary assignments, while sheaves enforce compatibility and uniqueness in gluing local data.
The Sheaf Condition Explained
The sheaf condition ensures that local data defined on overlapping open sets can be uniquely glued together to form global data, addressing the limitations of presheaves that only assign data without guaranteeing consistency. In technical terms, a sheaf requires that for any open cover, sections over the whole set correspond exactly to compatible families of sections on each subset, satisfying both existence and uniqueness of amalgamations. This condition transforms a presheaf into a sheaf by enforcing the ability to reconstruct information globally from compatible local pieces.
Importance of Sheafification
Sheafification transforms a presheaf, which may lack local gluing properties, into a sheaf that ensures consistent data reconstruction from local sections. This process is crucial for applications in algebraic geometry and topology where local-to-global principles underpin the structure of schemes and continuous functions. Without sheafification, the utility of presheaves is limited, as they cannot guarantee the coherence needed for many mathematical and physical interpretations.
Applications in Topology and Algebraic Geometry
Presheaves provide a flexible framework for assigning algebraic data to open sets, enabling local-to-global analysis crucial in topology and algebraic geometry, but they may lack the necessary gluing property to ensure consistency across intersections. Sheaves refine presheaves by enforcing patching conditions that guarantee local data can be uniquely amalgamated into global sections, making them indispensable for studying cohomology, sheafification processes, and reconstructing spaces from local information. Their applications include characterizing continuous functions, differential forms, and constructing etale cohomology, which underpins proofs of major theorems like the Weil conjectures and supports modern schemes in algebraic geometry.
Presheaf and Sheaf Morphisms
Presheaf morphisms are natural transformations between presheaves, defined by component maps that respect restriction maps but do not necessarily satisfy the gluing conditions. Sheaf morphisms are special cases of presheaf morphisms where these transformations preserve the sheaf axioms, ensuring local data uniquely determines global data. The distinction is crucial for applications in algebraic geometry and topology, where sheaf morphisms maintain consistency in passing from local to global information.
Common Misconceptions and Pitfalls
Presheaves are often mistakenly treated as sheaves, causing confusion about the essential gluing and locality conditions that distinguish sheaves. A common pitfall is assuming every compatible family of local sections in a presheaf uniquely glues to a global section, which only holds true for sheaves. Clarifying this distinction is crucial for accurately applying sheaf theory in topology and algebraic geometry.
Summary and Further Reading
Presheaves assign data to open sets without the requirement of gluing, while sheaves impose conditions ensuring local data uniquely determines global data, making sheaves essential in topology, algebraic geometry, and logic. Understanding this distinction is crucial for applications involving local-to-global principles and cohomology theories. For deeper insight, consult "Sheaves in Geometry and Logic" by Mac Lane and Moerdijk, and Hartshorne's "Algebraic Geometry" chapter on sheaves.
Presheaf Infographic
 libterm.com
libterm.com