Maximal surfaces are spacelike hypersurfaces in Lorentzian geometry characterized by zero mean curvature, representing critical points of the area functional. They play a crucial role in general relativity and the theory of minimal surfaces, offering insights into the geometry of spacetime. Explore the rest of this article to understand how maximal surfaces influence contemporary mathematical physics.
Table of Comparison
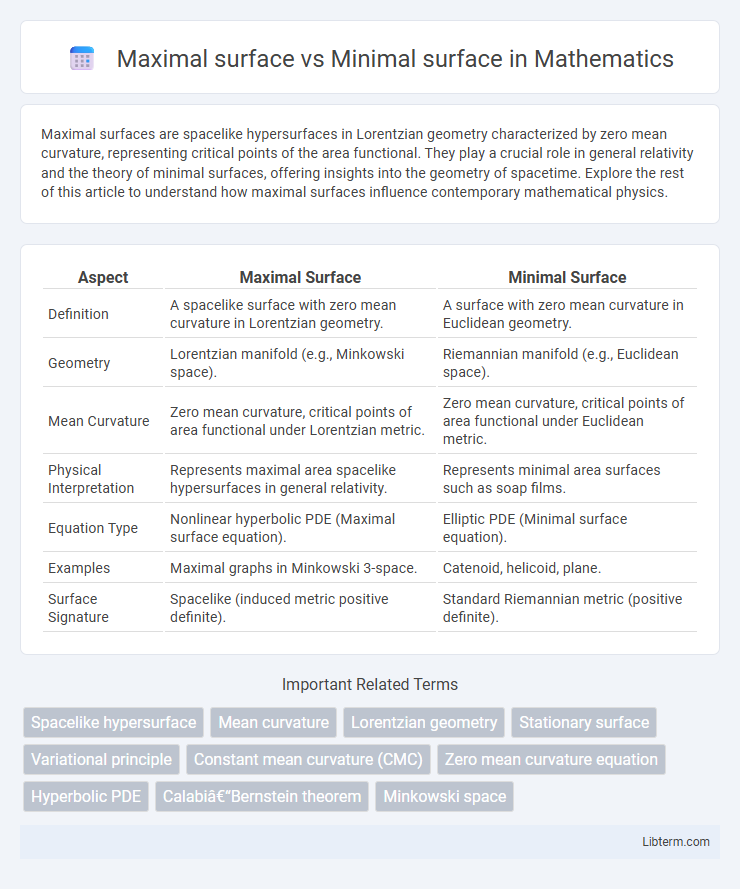
| Aspect | Maximal Surface | Minimal Surface |
|---|---|---|
| Definition | A spacelike surface with zero mean curvature in Lorentzian geometry. | A surface with zero mean curvature in Euclidean geometry. |
| Geometry | Lorentzian manifold (e.g., Minkowski space). | Riemannian manifold (e.g., Euclidean space). |
| Mean Curvature | Zero mean curvature, critical points of area functional under Lorentzian metric. | Zero mean curvature, critical points of area functional under Euclidean metric. |
| Physical Interpretation | Represents maximal area spacelike hypersurfaces in general relativity. | Represents minimal area surfaces such as soap films. |
| Equation Type | Nonlinear hyperbolic PDE (Maximal surface equation). | Elliptic PDE (Minimal surface equation). |
| Examples | Maximal graphs in Minkowski 3-space. | Catenoid, helicoid, plane. |
| Surface Signature | Spacelike (induced metric positive definite). | Standard Riemannian metric (positive definite). |
Introduction to Maximal and Minimal Surfaces
Maximal surfaces arise as spacelike hypersurfaces in Lorentzian manifolds with zero mean curvature, contrasting minimal surfaces that minimize area in Euclidean space with zero mean curvature. Both are critical points of area functionals but differ fundamentally due to the ambient metric signature; maximal surfaces maximize area under timelike constraints, while minimal surfaces minimize area under spatial constraints. These geometric objects are key in differential geometry and general relativity, capturing fundamental extremal properties of surfaces in distinct metric settings.
Defining Minimal Surfaces
Minimal surfaces are defined as surfaces that locally minimize area and have zero mean curvature at every point, making them critical points for the area functional. They arise naturally in calculus of variations and geometric measure theory, characterized by their harmonic coordinate functions satisfying Laplace's equation. In contrast, maximal surfaces in Lorentzian geometry maximize area in a spacelike hypersurface context, distinguished by having zero mean curvature under a Lorentzian metric rather than the Euclidean metric typical for minimal surfaces.
Understanding Maximal Surfaces
Maximal surfaces are spacelike hypersurfaces in Lorentzian geometry characterized by having zero mean curvature, analogous to minimal surfaces in Euclidean geometry but within a spacetime framework. They arise naturally in general relativity as models of spacelike slices with extremal area properties, often studied via the maximal surface equation, a nonlinear partial differential equation. Understanding maximal surfaces involves analyzing their geometric properties, stability conditions, and the role they play in the maximal slicing of spacetimes, contrasting with minimal surfaces that minimize area in Riemannian manifolds.
Mathematical Foundations
Maximal surfaces are spacelike hypersurfaces in Lorentzian geometry characterized by zero mean curvature in a pseudo-Riemannian manifold, often studied within General Relativity, while minimal surfaces are defined by zero mean curvature in Riemannian manifolds and arise in classic differential geometry. The mathematical foundation of minimal surfaces involves the calculus of variations and elliptic partial differential equations, whereas maximal surfaces correspond to solutions of hyperbolic PDEs under Lorentzian metrics. Both concepts extend the notion of extremal surfaces but differ fundamentally due to the signature of the ambient metric, influencing their curvature properties and stability criteria.
Key Differences Between Maximal and Minimal Surfaces
Maximal surfaces are spacelike surfaces in Lorentzian geometry with zero mean curvature and a positive definite induced metric, whereas minimal surfaces arise in Riemannian geometry as surfaces minimizing area with zero mean curvature and a positive definite induced metric. Key differences include the ambient space: maximal surfaces exist in Lorentz-Minkowski space, while minimal surfaces appear in Euclidean space. Physically, maximal surfaces relate to spacetime models and general relativity, whereas minimal surfaces model soap films and surface tension phenomena.
Physical and Geometric Applications
Maximal surfaces, characterized by zero mean curvature in Lorentzian geometry, play a critical role in general relativity and the modeling of spacetime hypersurfaces with maximal volume properties. Minimal surfaces, defined by zero mean curvature in Euclidean space, are extensively used in material science and architecture for their minimal area and optimal structural stability. Both surfaces provide essential insights into geometric analysis, influencing the design of minimal energy configurations and optimizing physical phenomena such as soap films and membrane shapes.
Notable Examples in Nature and Engineering
Maximal surfaces, characterized by zero mean curvature in Lorentzian geometry, appear in physics models such as black hole event horizons and soap films stretched across specific spacetime configurations. Minimal surfaces, with zero mean curvature in Euclidean space, are exemplified by natural structures like soap films, spider webs, and cellular membranes, which optimize surface area and energy. Engineering applications of minimal surfaces include lightweight architectural designs and membrane structures, while maximal surfaces contribute to relativistic models and material science simulations involving spacetime geometries.
Analytical Methods for Surface Analysis
Maximal surfaces and minimal surfaces are characterized by their geometrical properties, with maximal surfaces representing spacelike hypersurfaces having zero mean curvature in Lorentzian geometry, while minimal surfaces minimize area with zero mean curvature in Euclidean spaces. Analytical methods for surface analysis involve differential geometry techniques such as solving the Plateau problem using calculus of variations, employing partial differential equations like the minimal surface equation and the maximal surface equation derived from the vanishing mean curvature condition. Tools such as complex analysis, Weierstrass-Enneper parameterizations, and numerical methods including finite element methods facilitate precise determination and optimization of these surfaces in both theoretical and applied contexts.
Challenges in Surface Optimization
Maximal surfaces, characterized by zero mean curvature in Lorentzian manifolds, present unique challenges in optimization due to their indefinite metric, which complicates stability analysis and variational methods compared to minimal surfaces that minimize area in Euclidean spaces. The primary difficulty lies in handling the hyperbolic nature of maximal surfaces, leading to complex partial differential equations that lack the straightforward elliptic properties available for minimal surfaces. Additionally, numerical methods for maximal surfaces require careful treatment of boundary conditions and singularities, making computational algorithms more intricate than those used in minimal surface optimization.
Future Directions in Surface Geometry Research
Exploring maximal surfaces in Lorentzian manifolds alongside minimal surfaces in Euclidean spaces reveals distinct geometric and physical properties that drive innovative research directions. Future studies emphasize the development of advanced analytical methods and computational models to understand singularities and stability under varying curvature constraints. Integrating these insights promises breakthroughs in theoretical physics, material science, and geometric analysis.
Maximal surface Infographic
 libterm.com
libterm.com