Streckung refers to the process of stretching or elongating a material, commonly used in textiles, manufacturing, and physical training. Understanding the effects of Streckung on the properties and performance of fabrics or muscles can help optimize durability and flexibility. Explore this article to learn how Streckung impacts various applications and benefits your specific needs.
Table of Comparison
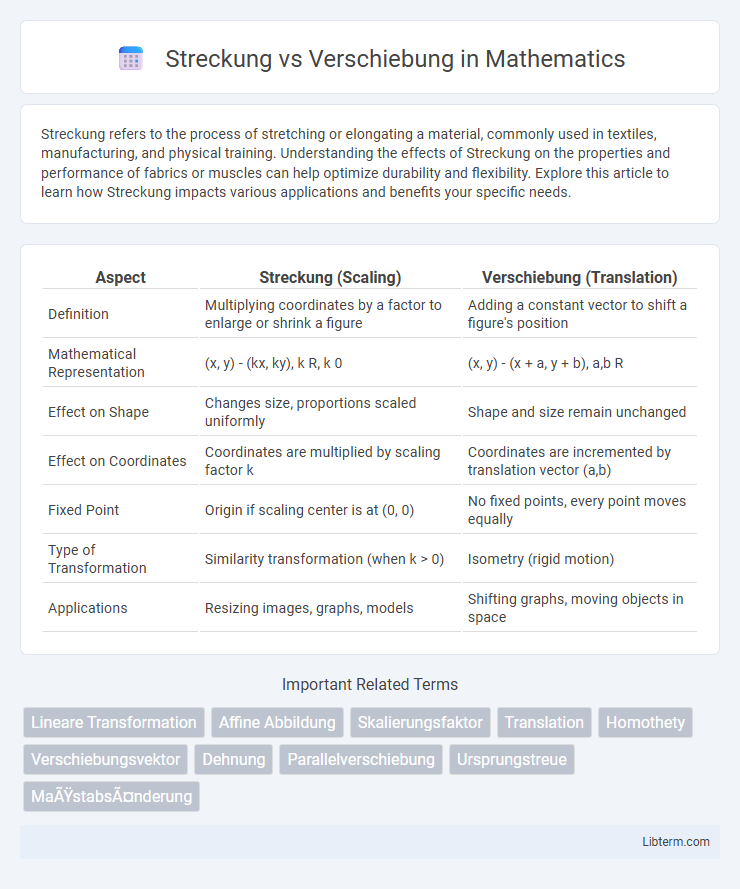
| Aspect | Streckung (Scaling) | Verschiebung (Translation) |
|---|---|---|
| Definition | Multiplying coordinates by a factor to enlarge or shrink a figure | Adding a constant vector to shift a figure's position |
| Mathematical Representation | (x, y) - (kx, ky), k R, k 0 | (x, y) - (x + a, y + b), a,b R |
| Effect on Shape | Changes size, proportions scaled uniformly | Shape and size remain unchanged |
| Effect on Coordinates | Coordinates are multiplied by scaling factor k | Coordinates are incremented by translation vector (a,b) |
| Fixed Point | Origin if scaling center is at (0, 0) | No fixed points, every point moves equally |
| Type of Transformation | Similarity transformation (when k > 0) | Isometry (rigid motion) |
| Applications | Resizing images, graphs, models | Shifting graphs, moving objects in space |
Einführung in Streckung und Verschiebung
Streckung and Verschiebung are fundamental geometric transformations used to manipulate figures in the coordinate plane. Streckung involves scaling a figure from a fixed center point by a specific factor, altering its size while preserving shape. Verschiebung, or translation, shifts a figure by a given vector without changing its size or orientation, maintaining congruence with the original shape.
Definition: Was ist eine Streckung?
Eine Streckung ist eine geometrische Transformation, bei der Punkte relativ zu einem festen Punkt, dem Streckzentrum, entlang einer bestimmten Richtung so verschoben werden, dass Abstande vom Zentrum vergrossert oder verkleinert werden. Dabei wird ein Streckfaktor verwendet, der angibt, wie stark die Figur gedehnt oder gestaucht wird, wobei Werte grosser als eins eine Vergrosserung und Werte zwischen null und eins eine Verkleinerung bedeuten. Im Gegensatz zur Verschiebung verandert die Streckung die Grosse der Figur, wahrend ihre Form erhalten bleibt.
Definition: Was ist eine Verschiebung?
Eine Verschiebung ist eine geometrische Transformation, bei der alle Punkte einer Figur oder eines Objekts um denselben Vektor parallel verschoben werden, ohne Form oder Grosse zu verandern. Diese Translation bewahrt Abstande und Winkel, was bedeutet, dass das Bild kongruent zum Original bleibt. Die Verschiebung wird durch einen Verschiebungsvektor beschrieben, der die Richtung und den Abstand der Bewegung angibt.
Mathematische Grundlagen: Unterschiede erkennen
Streckung und Verschiebung sind fundamentale Transformationen in der analytischen Geometrie, die unterschiedliche Auswirkungen auf Koordinaten und Funktionen haben. Streckung verandert die Abstande zum Ursprung durch Multiplikation der Koordinaten mit einem Faktor grosser oder kleiner als eins, wahrend Verschiebung die Position einer Figur durch Addition eines Vektors zu allen Punkten verschiebt. Mathematisch lasst sich Streckung durch lineare Abbildung \( f(x) = kx \) mit Skalar \( k \neq 0 \) und Verschiebung durch Translation \( f(x) = x + v \) mit Vektor \( v \in \mathbb{R}^n \) beschreiben, wobei die Streckung Skalenanderungen und die Verschiebung Ortsveranderungen reprasentiert.
Grafische Darstellung: Streckung vs Verschiebung
In der grafischen Darstellung zeigt eine Streckung eine Skalierung der Kurve entlang der y-Achse oder x-Achse, wodurch die Funktion proportional grosser oder kleiner wird, wahrend bei einer Verschiebung die Kurve parallel entlang der Achsen verschoben wird, ohne die Form zu verandern. Streckungen werden durch Multiplikation der Funktionswerte mit einem Faktor \( a \) beschrieben, z.B. \( f(x) \rightarrow a \cdot f(x) \), wahrend Verschiebungen durch Addition oder Subtraktion eines Wertes entweder in \( x \)-Richtung \( (x \rightarrow x + c) \) oder \( y \)-Richtung \( (f(x) \rightarrow f(x) + d) \) erfolgen. Die visuelle Differenz zeigt sich klar darin, dass bei Streckungen die Amplitude der Funktion variiert, wahrend bei Verschiebungen die gesamte Kurve ohne Anderung des Amplitudenverhaltnisses ihre Position verandert.
Anwendungsgebiete in der Mathematik
Streckung und Verschiebung sind fundamentale Transformationen in der Mathematik, insbesondere in der Geometrie und der linearen Algebra. Streckungen verandern die Grosse von Figuren oder Funktionen ohne Formverzerrung und finden Anwendung in der Skalierung von Objekten sowie bei der Analyse von Funktionen durch Streckungsfaktoren. Verschiebungen, auch Translationen genannt, verschieben Objekte im Koordinatensystem ohne Rotation oder Grossenanderung, was in Bereichen wie der Vektoranalysis, der Geometrie und der Graphentheorie essenziell ist.
Praxisbeispiele zur Veranschaulichung
Streckung (scaling) verandert die Grosse einer Figur proportional zu einem Skalierungsfaktor, beispielsweise beim Vergrossern eines Bauplans, wahrend die Verschiebung (Translation) alle Punkte einer Figur um einen festen Vektor verschiebt, wie beim Verschieben eines Mobelstucks in einem Raum. Ein Praxisbeispiel fur Streckung ist das Vergrossern eines Fotos, bei dem alle Abstande multipliziert werden, wodurch die Form erhalten bleibt, aber die Masse wachsen. Bei der Verschiebung bleibt die Grosse und Form unverandert, nur die Position andert sich, wie beim Verschieben eines Diagramms auf einer Folie ohne Verzerrung.
Gemeinsamkeiten und Unterschiede im Überblick
Streckung und Verschiebung sind grundlegende Transformationen in der Geometrie, die Punktmengen im Koordinatensystem verandern, wobei die Streckung die Abstande zum Ursprung skaliert und die Verschiebung die Lage der Punkte um einen festen Vektor verschiebt. Beide Transformationen erhalten die Form der Figuren, unterscheiden sich jedoch darin, dass Streckungen Grossenanderungen verursachen, wahrend Verschiebungen die Form und Grosse unverandert lassen. In der linearen Algebra werden Streckungen durch Multiplikation mit einer Skalarmatrix dargestellt, wahrend Verschiebungen durch Addition eines Vektors realisiert werden.
Häufige Fehler und Missverständnisse
Streckung und Verschiebung werden oft verwechselt, da beide Transformationen die Lage oder Grosse von Figuren verandern, aber unterschiedlich wirken: Streckung verandert die Grosse durch einen Streckfaktor, wahrend Verschiebung die Position ohne Grossenanderung verschiebt. Haufige Fehler entstehen, wenn Verschiebungen als Skalierungen interpretiert werden oder Streckungen falschlich als Translationen angesehen werden. Missverstandnisse treten auch auf, wenn der Ursprung der Transformation nicht klar definiert ist, was besonders bei Streckungen die Figur verzerren kann.
Fazit: Wann Streckung, wann Verschiebung?
Streckung occurs when scaling a figure by multiplying its coordinates with a factor greater than one, resulting in an enlargement maintaining shape proportions. Verschiebung refers to shifting a figure without altering its size or shape, moving it linearly along vectors in the coordinate plane. Use Streckung when modifying size and Verschiebung to reposition without distortion.
Streckung Infographic
 libterm.com
libterm.com