The moduli space is a geometric framework that classifies mathematical objects, such as algebraic curves or vector bundles, by their intrinsic properties and symmetries. It provides a powerful tool to understand the structure and relationships of complex systems in algebraic geometry and theoretical physics. Explore the rest of the article to see how moduli spaces impact modern mathematical research and applications.
Table of Comparison
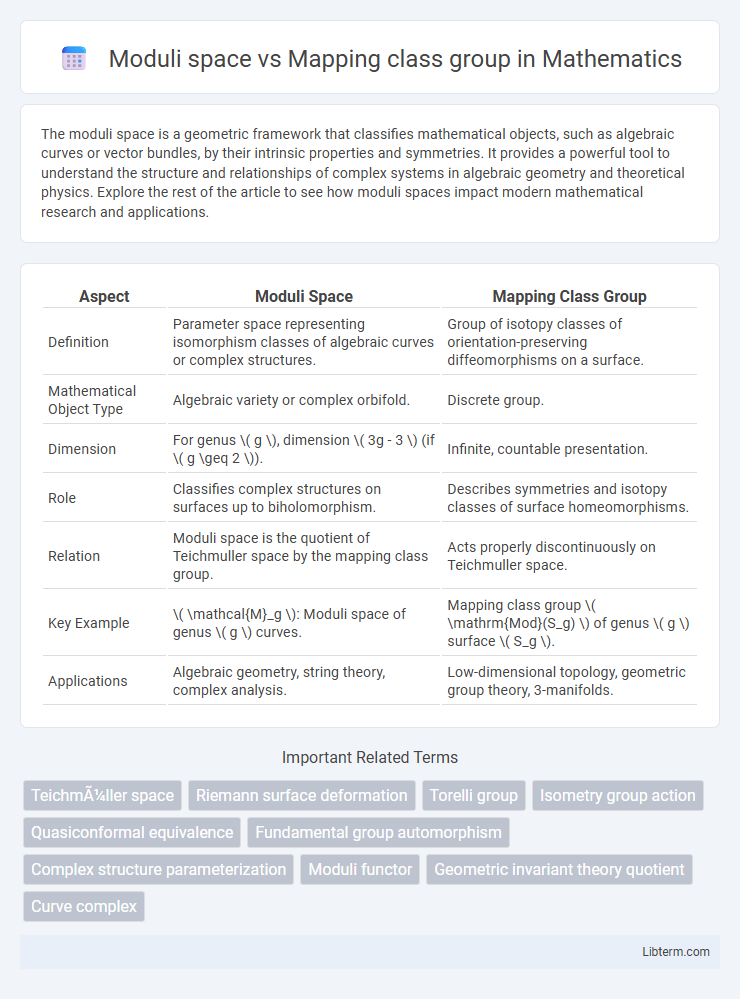
| Aspect | Moduli Space | Mapping Class Group |
|---|---|---|
| Definition | Parameter space representing isomorphism classes of algebraic curves or complex structures. | Group of isotopy classes of orientation-preserving diffeomorphisms on a surface. |
| Mathematical Object Type | Algebraic variety or complex orbifold. | Discrete group. |
| Dimension | For genus \( g \), dimension \( 3g - 3 \) (if \( g \geq 2 \)). | Infinite, countable presentation. |
| Role | Classifies complex structures on surfaces up to biholomorphism. | Describes symmetries and isotopy classes of surface homeomorphisms. |
| Relation | Moduli space is the quotient of Teichmuller space by the mapping class group. | Acts properly discontinuously on Teichmuller space. |
| Key Example | \( \mathcal{M}_g \): Moduli space of genus \( g \) curves. | Mapping class group \( \mathrm{Mod}(S_g) \) of genus \( g \) surface \( S_g \). |
| Applications | Algebraic geometry, string theory, complex analysis. | Low-dimensional topology, geometric group theory, 3-manifolds. |
Introduction to Moduli Space and Mapping Class Group
Moduli space parametrizes equivalence classes of complex structures on a given topological surface, encoding geometric deformations up to isomorphism. The mapping class group consists of isotopy classes of orientation-preserving diffeomorphisms of a surface, acting naturally on the moduli space by changing the marking of complex structures. Understanding this interplay links algebraic geometry, topology, and complex analysis, revealing deep structures of surfaces and their moduli.
Defining Moduli Spaces in Geometry
Moduli spaces classify geometric structures up to an equivalence relation, often parameterizing complex structures on surfaces. These spaces are closely linked to the mapping class group, which acts as the group of isotopy classes of diffeomorphisms of a surface, governing the symmetries and identifications within the moduli space. Defining moduli spaces involves understanding quotient constructions of Teichmuller space by the mapping class group, resulting in rich geometric and algebraic structures central to algebraic geometry and low-dimensional topology.
Understanding the Mapping Class Group
The Mapping Class Group (MCG) of a surface is the group of isotopy classes of orientation-preserving diffeomorphisms, playing a fundamental role in the study of Moduli space by encoding its symmetries and geometric transformations. Understanding the MCG involves analyzing its algebraic structure, generators such as Dehn twists, and its action on Teichmuller space, which serves as a universal cover for Moduli space. This interplay enables the classification of complex structures on surfaces and provides insights into the topology of Moduli spaces of Riemann surfaces.
Historical Context and Development
The study of the moduli space of Riemann surfaces originates from Bernhard Riemann's 19th-century work on complex analysis and algebraic curves, providing a parameter space for complex structures. The mapping class group, introduced later in the 20th century by Max Dehn and Jakob Nielsen, captures the isotopy classes of surface homeomorphisms, playing a crucial role in understanding the symmetries of moduli spaces. The interplay between moduli spaces and mapping class groups became foundational in Teichmuller theory, with contributions from Lars Ahlfors, Lipman Bers, and William Thurston shaping the modern geometric and topological framework.
Key Differences Between Moduli Space and Mapping Class Group
Moduli space parametrizes equivalence classes of geometric structures on a surface, capturing complex structures up to isomorphism, whereas the mapping class group consists of isotopy classes of orientation-preserving diffeomorphisms acting on the surface. The moduli space is a geometric object often realized as an orbifold or algebraic variety, while the mapping class group is a discrete group encoding symmetries and self-homeomorphisms of the surface. Key differences include the moduli space's role as a parameter space for complex structures compared to the mapping class group's role as a group of topological symmetries influencing the structure of moduli spaces through its group action.
Interrelations: Moduli Spaces as Quotients by Mapping Class Groups
Moduli spaces of Riemann surfaces arise as quotients of Teichmuller spaces by the action of the mapping class group, capturing complex structures up to isotopy. The mapping class group acts properly discontinuously on Teichmuller space, and this quotient construction encodes equivalence classes of conformal structures, highlighting the deep geometric and algebraic interplay. Understanding this relationship is fundamental for studying the topology of moduli spaces, their orbifold structures, and the associated representation theory of mapping class groups.
Algebraic Properties and Structures
The Moduli space of Riemann surfaces encapsulates complex algebraic structures reflecting deformations of conformal equivalence classes, while the Mapping class group acts as the fundamental symmetry group governing these deformations through isotopy classes of orientation-preserving diffeomorphisms. Algebraically, the Mapping class group is finitely presented and exhibits rich structures such as the Torelli subgroup, which corresponds to automorphisms acting trivially on homology, influencing the geometry of the Moduli space via quotient constructions. Cohomological properties of both entities reveal deep connections to Teichmuller theory, where the Moduli space represents an orbifold quotient by the Mapping class group, embedding algebraic topology into the study of complex structures.
Applications in Mathematics and Physics
The moduli space, representing equivalence classes of algebraic curves or complex structures, plays a crucial role in string theory by parametrizing possible shapes of the universe's extra dimensions, while the mapping class group governs the symmetries of surfaces and acts as the fundamental group of the moduli space, controlling its topological and geometric properties. In mathematics, this interplay aids in understanding Teichmuller theory, low-dimensional topology, and algebraic geometry through classification problems, deformation theory, and monodromy representations. Furthermore, applications in quantum field theory and conformal field theory exploit these structures to analyze moduli-dependent partition functions and gauge symmetries, bridging abstract geometry with physical phenomena.
Recent Advances and Research Directions
Recent advances in the study of Moduli spaces and Mapping class groups have highlighted their intricate relationship through the lens of Teichmuller theory and geometric group theory. Cutting-edge research explores the dynamics of Mapping class groups acting on various Moduli spaces, revealing new structural properties and connections to low-dimensional topology and algebraic geometry. Emerging directions involve the application of higher Teichmuller theory, quantum Moduli spaces, and the development of computational tools to analyze their complex interactions.
Future Perspectives and Open Problems
Exploring the future perspectives of moduli space versus mapping class group reveals significant challenges in understanding the interplay between geometric structures and group actions on surfaces, particularly in higher dimensions and complex settings. Open problems include classifying the dynamics of mapping class group actions on various moduli spaces and extending the connections to quantum invariants and Teichmuller theory. Advancements in computational methods and categorical frameworks hold potential for breakthroughs in characterizing the global structure of moduli spaces informed by mapping class group symmetries.
Moduli space Infographic
 libterm.com
libterm.com