A complex manifold is a topological space that locally resembles complex Euclidean space and allows for the definition of holomorphic functions. These structures play a crucial role in complex geometry, differential geometry, and mathematical physics, providing a rich framework to study complex variables in higher dimensions. Discover how complex manifolds impact various scientific fields by exploring the rest of the article.
Table of Comparison
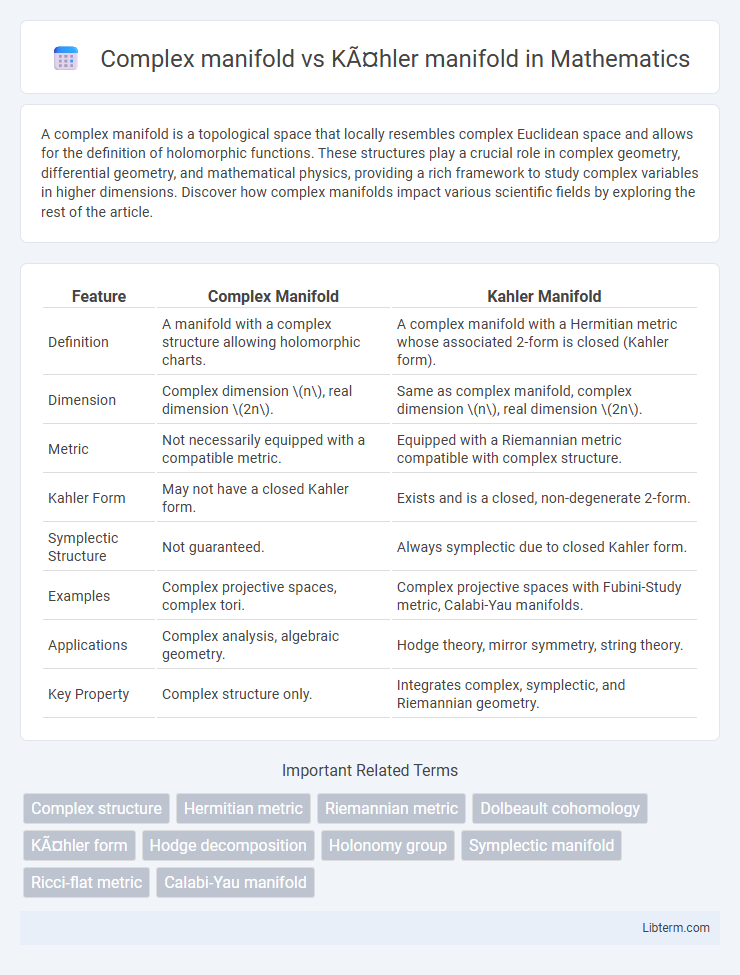
| Feature | Complex Manifold | Kahler Manifold |
|---|---|---|
| Definition | A manifold with a complex structure allowing holomorphic charts. | A complex manifold with a Hermitian metric whose associated 2-form is closed (Kahler form). |
| Dimension | Complex dimension \(n\), real dimension \(2n\). | Same as complex manifold, complex dimension \(n\), real dimension \(2n\). |
| Metric | Not necessarily equipped with a compatible metric. | Equipped with a Riemannian metric compatible with complex structure. |
| Kahler Form | May not have a closed Kahler form. | Exists and is a closed, non-degenerate 2-form. |
| Symplectic Structure | Not guaranteed. | Always symplectic due to closed Kahler form. |
| Examples | Complex projective spaces, complex tori. | Complex projective spaces with Fubini-Study metric, Calabi-Yau manifolds. |
| Applications | Complex analysis, algebraic geometry. | Hodge theory, mirror symmetry, string theory. |
| Key Property | Complex structure only. | Integrates complex, symplectic, and Riemannian geometry. |
Introduction to Complex Manifolds
A complex manifold is a topological space that locally resembles complex Euclidean space and is equipped with a holomorphic atlas, enabling the study of complex-analytic structures. Kahler manifolds form a special class of complex manifolds endowed with a Hermitian metric whose associated 2-form is closed, integrating complex, symplectic, and Riemannian geometry. The foundational theory of complex manifolds involves complex charts, holomorphic transition functions, and complex dimension, laying the groundwork for exploring rich geometric properties exhibited by Kahler manifolds.
Key Properties of Complex Manifolds
Complex manifolds are smooth manifolds with a holomorphic atlas, enabling local complex coordinate charts and holomorphic transition functions, which endow them with an integrable almost complex structure. Key properties include the existence of holomorphic tangent bundles and complex differential forms, supporting rich analytic and geometric structures. In contrast, Kahler manifolds possess all complex manifold properties plus a Hermitian metric whose associated (1,1)-form is closed, yielding a symplectic structure that tightly links complex, Riemannian, and symplectic geometry.
Understanding Kähler Manifolds
Kahler manifolds are a special class of complex manifolds equipped with a Hermitian metric whose associated 2-form is closed, making it both symplectic and complex-compatible. This closed 2-form, known as the Kahler form, satisfies the integrability condition that links the complex structure, metric, and symplectic form, providing a rich geometric framework. Understanding Kahler manifolds involves studying their Hodge theory, Ricci curvature, and role in complex differential geometry and algebraic geometry, distinguishing them from general complex manifolds that lack this compatibility between metric and symplectic structure.
Core Characteristics of Kähler Manifolds
Kahler manifolds are complex manifolds equipped with a Hermitian metric whose associated (1,1)-form is closed, satisfying the Kahler condition that unifies complex structure, Riemannian metric, and symplectic form. This closedness property leads to rich geometric and topological features, such as the existence of harmonic representatives for cohomology classes and the decomposition of the Laplacian. Complex manifolds without this closed (1,1)-form lack the integrative structure that defines Kahler geometry, making Kahler manifolds a special and highly structured subclass within complex geometry.
Major Differences between Complex and Kähler Manifolds
Complex manifolds are differentiable manifolds equipped with an atlas of charts to the complex plane such that the transition maps are holomorphic, defining a complex structure without further geometric constraints. Kahler manifolds, a special subclass of complex manifolds, possess a Hermitian metric whose associated 2-form is closed, integrating complex structure, symplectic structure, and Riemannian metric into a compatible triple. The major difference lies in the additional geometric condition on Kahler manifolds requiring the Kahler form to be closed, which endows them with rich geometric and topological properties not generally present in complex manifolds.
Holomorphic Structures and Their Roles
Complex manifolds possess holomorphic structures defined by transition maps that are holomorphic functions, enabling the study of complex-analytic properties locally. Kahler manifolds enhance this framework by integrating a Hermitian metric whose associated (1,1)-form is closed, establishing a powerful link between complex geometry, symplectic structures, and Riemannian metrics. The holomorphic structures in Kahler manifolds facilitate Hodge theory applications and allow for deeper exploration of cohomological invariants and curvature properties central to complex differential geometry.
Metrics and Forms: Hermitian vs Kähler
Complex manifolds are equipped with Hermitian metrics, which combine a Riemannian metric and a compatible complex structure, allowing for the measurement of lengths and angles but not necessarily closed forms. Kahler manifolds possess a special type of Hermitian metric called a Kahler metric, characterized by a symplectic form that is both Hermitian and closed, yielding powerful geometric and topological properties. The Kahler form, a closed, positive (1,1)-form, distinguishes Kahler manifolds from general complex manifolds by ensuring integrability and richer curvature relations.
Examples of Complex and Kähler Manifolds
Complex manifolds include examples such as complex projective spaces, complex tori, and complex algebraic varieties, which serve as fundamental objects in complex geometry. Kahler manifolds, a special class of complex manifolds, include complex projective spaces equipped with the Fubini-Study metric and Calabi-Yau manifolds, characterized by their rich geometric structure combining symplectic, complex, and Riemannian properties. While every Kahler manifold is a complex manifold, notable examples like Hopf surfaces demonstrate complex manifolds that lack any Kahler metric, highlighting the distinctions in their geometric frameworks.
Applications in Mathematics and Physics
Complex manifolds serve as the foundational structures in several branches of mathematics and theoretical physics, enabling the study of complex analytic functions and holomorphic mappings crucial for algebraic geometry and string theory. Kahler manifolds, as special complex manifolds equipped with a symplectic form compatible with their complex structure, play a vital role in gauge theory, mirror symmetry, and the study of moduli spaces in both mathematics and quantum field theory. Their rich geometric properties facilitate the formulation of supersymmetric models and provide powerful tools for understanding Calabi-Yau manifolds in compactification scenarios of string theory.
Summary: Choosing Between Complex and Kähler Manifolds
Complex manifolds are differentiable manifolds with a holomorphic atlas, allowing complex coordinate transitions, while Kahler manifolds are special complex manifolds equipped with a Hermitian metric whose associated 2-form is closed, combining complex, symplectic, and Riemannian structures. The choice between complex and Kahler manifolds depends on the additional geometric and topological properties required, as Kahler manifolds offer richer structure beneficial for problems in algebraic geometry and theoretical physics. When a closed symplectic form compatible with the complex structure is essential, Kahler manifolds provide the necessary framework beyond the general flexibility of complex manifolds.
Complex manifold Infographic
 libterm.com
libterm.com