The Hilbert transform is a fundamental tool in signal processing used to derive the analytic representation of real-valued signals, enabling the extraction of instantaneous amplitude and phase information. It shifts the phase of each frequency component by 90 degrees, producing the quadrature component essential for envelope detection and modulation analysis. Explore the rest of the article to understand how your applications can benefit from this powerful mathematical technique.
Table of Comparison
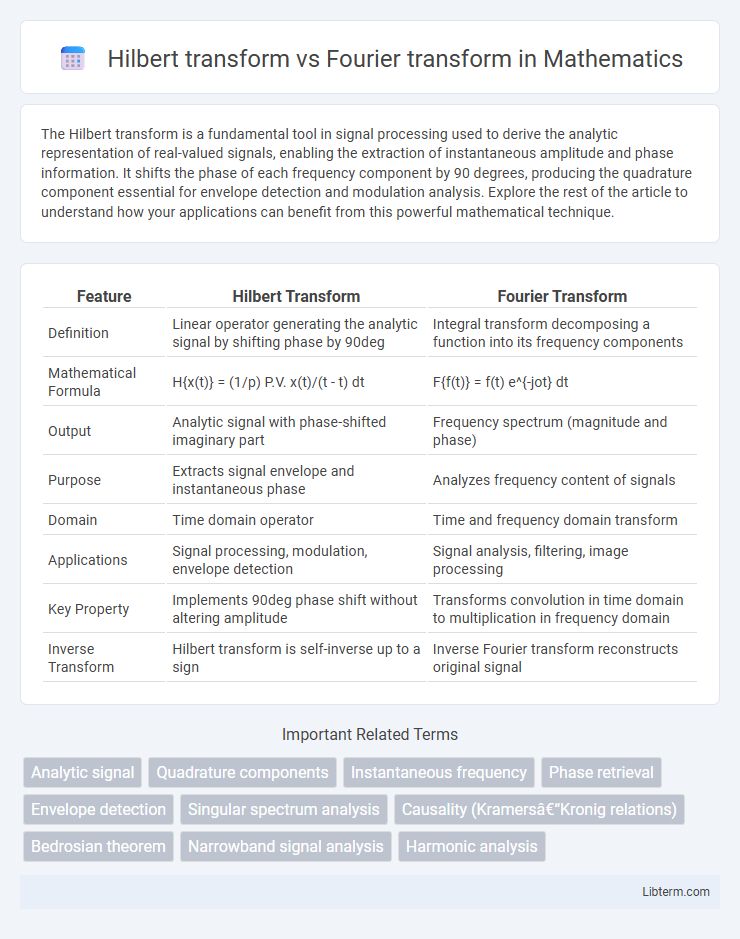
| Feature | Hilbert Transform | Fourier Transform |
|---|---|---|
| Definition | Linear operator generating the analytic signal by shifting phase by 90deg | Integral transform decomposing a function into its frequency components |
| Mathematical Formula | H{x(t)} = (1/p) P.V. x(t)/(t - t) dt | F{f(t)} = f(t) e^{-jot} dt |
| Output | Analytic signal with phase-shifted imaginary part | Frequency spectrum (magnitude and phase) |
| Purpose | Extracts signal envelope and instantaneous phase | Analyzes frequency content of signals |
| Domain | Time domain operator | Time and frequency domain transform |
| Applications | Signal processing, modulation, envelope detection | Signal analysis, filtering, image processing |
| Key Property | Implements 90deg phase shift without altering amplitude | Transforms convolution in time domain to multiplication in frequency domain |
| Inverse Transform | Hilbert transform is self-inverse up to a sign | Inverse Fourier transform reconstructs original signal |
Introduction to Signal Transformations
The Hilbert transform provides a way to generate the analytic signal by shifting the phase of all frequency components by 90 degrees, enabling instantaneous amplitude and phase analysis. The Fourier transform decomposes signals into their frequency components, representing them in the frequency domain for spectral analysis. Both transforms play crucial roles in signal processing, with the Fourier transform emphasizing frequency content and the Hilbert transform facilitating envelope detection and phase information extraction.
What is the Hilbert Transform?
The Hilbert Transform is a linear operator that shifts the phase of a signal by 90 degrees, creating its analytic representation crucial for envelope detection and instantaneous frequency analysis. Unlike the Fourier Transform, which decomposes signals into their frequency components, the Hilbert Transform provides a way to extract the signal's instantaneous amplitude and phase, enabling advanced signal processing techniques. This makes the Hilbert Transform essential in applications such as communication systems, biomedical signal analysis, and modulation theory.
What is the Fourier Transform?
The Fourier Transform is a mathematical operation that decomposes a time-domain signal into its constituent frequencies, representing the signal as a spectrum of sinusoidal components. It converts complex waveforms into a frequency-domain representation, enabling analysis of amplitude and phase information for each frequency component. Unlike the Hilbert Transform, which provides the analytic signal with a 90-degree phase shift, the Fourier Transform offers a comprehensive frequency spectrum critical for signal processing, communications, and system analysis.
Mathematical Foundations of Hilbert and Fourier Transforms
The Fourier transform decomposes a function into its constituent frequencies using complex exponentials, establishing a foundation in harmonic analysis and linear algebra. The Hilbert transform generates the analytic signal by shifting the phase of each frequency component by 90 degrees, relying on the Cauchy principal value integral and properties of harmonic conjugates in complex analysis. Both transforms are deeply connected through the Fourier domain, where the Hilbert transform corresponds to multiplication by the signum function, reflecting their intertwined mathematical structures.
Key Differences Between Hilbert and Fourier Transforms
The Hilbert transform generates the analytic signal by shifting the phase of all frequency components of a real-valued signal by 90 degrees, enabling instantaneous amplitude and phase analysis. The Fourier transform decomposes a signal into its constituent frequencies, providing magnitude and phase spectra across the entire frequency range. Key differences include the Hilbert transform's focus on producing a complex signal for envelope detection versus the Fourier transform's role in frequency domain representation and signal reconstruction.
Applications of the Hilbert Transform
The Hilbert transform finds extensive applications in signal processing, particularly for analytic signal generation where it aids in extracting instantaneous amplitude and phase information. It is widely used in communication systems to implement single sideband modulation and envelope detection for amplitude modulation signals. Moreover, the Hilbert transform plays a crucial role in biomedical engineering for analyzing electrocardiograms (ECG) and brain signals by enhancing feature extraction and noise reduction.
Applications of the Fourier Transform
The Fourier transform is extensively used in signal processing, enabling the decomposition of complex signals into their frequency components, which is critical for audio and image analysis. It also plays a vital role in solving partial differential equations by transforming them into algebraic equations in the frequency domain, simplifying complex problem-solving in physics and engineering. Applications extend to communications, where it aids in modulating and demodulating signals, and in medical imaging techniques like MRI, enhancing image reconstruction and analysis.
Hilbert vs Fourier Transform: Strengths and Limitations
The Hilbert transform excels in creating analytic signals and extracting instantaneous phase and amplitude, making it ideal for time-domain signal analysis and modulation systems. The Fourier transform provides comprehensive frequency-domain representation, enabling spectral analysis and filtering but lacks time-localization for non-stationary signals. While the Fourier transform offers global frequency information, the Hilbert transform delivers phase-shifted signal components crucial for envelope detection and instantaneous frequency estimation.
Practical Examples and Use Cases
The Hilbert transform is commonly used in signal processing for creating analytic signals, enabling envelope detection and instantaneous phase analysis in applications like amplitude modulation and seismic data interpretation. The Fourier transform excels in frequency domain analysis, filtering, and spectral decomposition, making it essential in audio signal processing, image compression, and communications. Both transforms complement each other, with Hilbert providing phase information and Fourier offering frequency content, crucial in radar signal analysis and biomedical engineering such as ECG signal processing.
Choosing the Right Transform for Your Needs
Hilbert transform emphasizes instantaneous phase and amplitude information, making it ideal for signal modulation and envelope extraction tasks. Fourier transform provides comprehensive frequency domain analysis, suitable for identifying dominant spectral components over time. Selecting the right transform depends on whether phase information or a global frequency spectrum is more critical for your signal processing application.
Hilbert transform Infographic
 libterm.com
libterm.com