Convex shapes curve outward, with every line segment between two points lying entirely inside the shape, which makes them fundamental in geometry and optimization problems. Understanding how convex properties influence structures and algorithms can enhance your problem-solving strategies and mathematical reasoning. Explore the rest of the article to discover the significance of convexity in various fields.
Table of Comparison
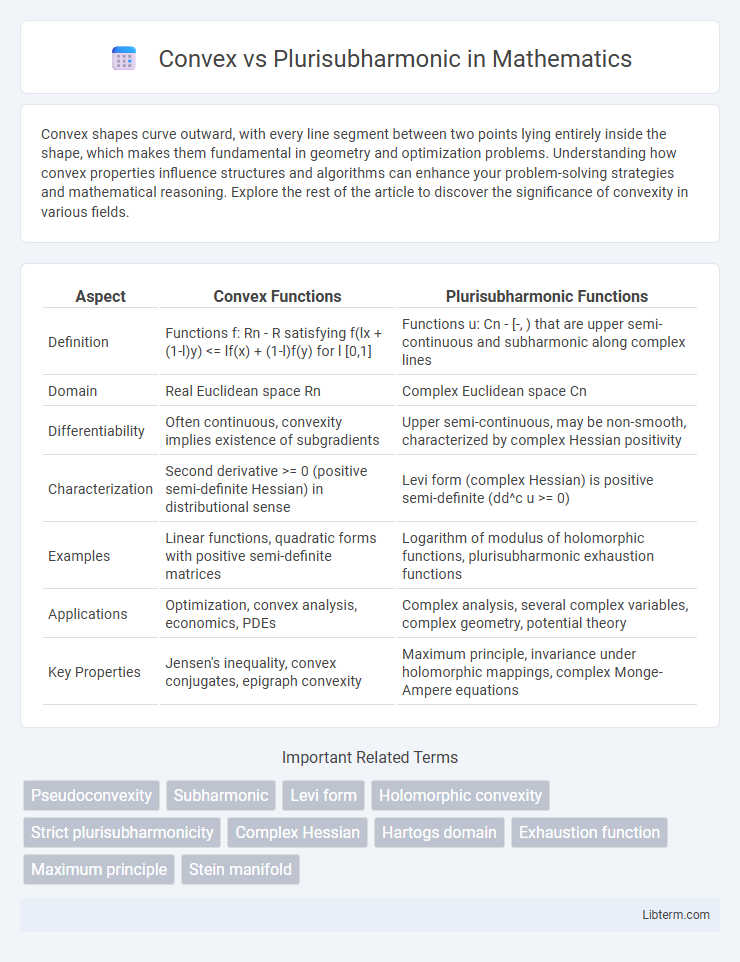
| Aspect | Convex Functions | Plurisubharmonic Functions |
|---|---|---|
| Definition | Functions f: Rn - R satisfying f(lx + (1-l)y) <= lf(x) + (1-l)f(y) for l [0,1] | Functions u: Cn - [-, ) that are upper semi-continuous and subharmonic along complex lines |
| Domain | Real Euclidean space Rn | Complex Euclidean space Cn |
| Differentiability | Often continuous, convexity implies existence of subgradients | Upper semi-continuous, may be non-smooth, characterized by complex Hessian positivity |
| Characterization | Second derivative >= 0 (positive semi-definite Hessian) in distributional sense | Levi form (complex Hessian) is positive semi-definite (dd^c u >= 0) |
| Examples | Linear functions, quadratic forms with positive semi-definite matrices | Logarithm of modulus of holomorphic functions, plurisubharmonic exhaustion functions |
| Applications | Optimization, convex analysis, economics, PDEs | Complex analysis, several complex variables, complex geometry, potential theory |
| Key Properties | Jensen's inequality, convex conjugates, epigraph convexity | Maximum principle, invariance under holomorphic mappings, complex Monge-Ampere equations |
Introduction to Convex and Plurisubharmonic Functions
Convex functions are defined on convex domains in real Euclidean spaces, characterized by the property that their epigraphs form convex sets, ensuring that the line segment between any two points on the graph lies above the function. Plurisubharmonic functions generalize convexity to complex variables, defined on complex manifolds with the property that their restriction to any complex line is subharmonic, playing a critical role in several complex variables and complex potential theory. Both classes of functions are essential in optimization and complex analysis, with convex functions focusing on real-valued domains, while plurisubharmonic functions analyze complex structures and potential applications.
Mathematical Definitions: Convexity vs Plurisubharmonicity
Convex functions are defined on real vector spaces and satisfy the inequality f(tx + (1 - t)y) <= tf(x) + (1 - t)f(y) for all x, y and t [0,1], ensuring their epigraphs form convex sets. Plurisubharmonic functions, defined on complex spaces Cn, require the function to be upper semi-continuous and subharmonic along every complex line, which means their restriction to any complex line is subharmonic. Convexity is a real-variable concept characterized by linear interpolation, whereas plurisubharmonicity generalizes subharmonicity to several complex variables with constraints related to complex analyticity and positivity of the complex Hessian.
Key Properties and Differences
Convex functions are real-valued functions defined on convex subsets of real vector spaces that satisfy the property \( f(\lambda x + (1-\lambda)y) \leq \lambda f(x) + (1-\lambda) f(y) \) for all \( x, y \) and \( \lambda \in [0,1] \), whereas plurisubharmonic functions are upper semi-continuous functions on complex manifolds that maintain subharmonicity along every complex line. Key properties distinguishing plurisubharmonic functions include their invariance under holomorphic changes of coordinates and their role in complex potential theory, particularly through the Levi form's semi-positivity, contrasting with the linear structure and second-order difference inequalities governing convexity. Plurisubharmonicity generalizes convexity into the complex setting, emphasizing complex Hessian positivity and enabling applications in several complex variables and complex geometry, unlike the strictly real setting of convex functions.
Geometric Interpretations
Convex functions define convex sets by ensuring that line segments between points on the graph lie above or on the graph, representing geometric convexity in real Euclidean spaces. Plurisubharmonic functions generalize convexity to complex variables, modeling subharmonicity in complex geometry by maintaining non-negativity of the complex Hessian and ensuring pseudoconvexity in complex manifolds. The geometric interpretation of plurisubharmonicity captures complex analytic convexity related to holomorphic function theory, contrasting with real-variable convex sets.
Role in Real vs Complex Analysis
Convex functions play a central role in real analysis by characterizing domains of minimization problems and ensuring properties like continuity and differentiability in Euclidean spaces. Plurisubharmonic functions extend these concepts to several complex variables, serving as key tools in complex analysis and complex geometry for describing pseudoconvex domains and aiding in the study of holomorphic functions. While convexity relies on linear inequalities in R^n, plurisubharmonicity involves complex Hessians and subharmonicity along complex lines, reflecting the richer structure of C^n.
Examples of Convex and Plurisubharmonic Functions
Convex functions like f(x) = x2 on the real line exhibit non-negative second derivatives, ensuring the function lies below any secant line connecting two points, while plurisubharmonic functions such as the logarithm of the modulus of a holomorphic function, u(z) = log|z| in complex analysis, maintain subharmonicity in every complex variable. Another example of a convex function is f(x) = e^x, which grows exponentially and maintains the convexity criterion via a positive second derivative. In contrast, functions like u(z) = |z|2 are plurisubharmonic since they are complex-valued and satisfy the condition of their complex Hessian being positive semi-definite.
Applications in Optimization and Complex Analysis
Convex functions play a central role in optimization due to their property of having global minima that are easier to identify, making them essential for solving diverse optimization problems efficiently. Plurisubharmonic functions, defined on complex domains, are crucial in complex analysis as they generalize subharmonic functions and are key tools in pluripotential theory and complex geometry. Their applications intersect in areas like complex optimization, where plurisubharmonicity ensures certain stability and convergence properties, bridging the gap between real convexity and complex analytic structures.
Criteria for Identifying Plurisubharmonicity
Plurisubharmonicity is identified through the requirement that a function must be upper semi-continuous and its restriction to any complex line is subharmonic, a stronger condition than convexity which applies to real-valued functions on convex domains. Unlike convex functions defined by the non-negativity of the Hessian matrix, plurisubharmonic functions satisfy the positivity of the complex Hessian matrix, specifically the Hermitian form associated with the complex second derivatives being positive semi-definite. This criterion ensures that plurisubharmonic functions naturally generalize subharmonic functions in several complex variables and serve as crucial tools in complex analysis and pluripotential theory.
Relationship with Harmonic and Subharmonic Functions
Convex functions and plurisubharmonic functions both generalize the notion of curvature but differ in their analytic contexts: convex functions are defined on real domains with nonnegative second derivatives, while plurisubharmonic functions are defined on complex domains and satisfy the complex Hessian's positivity in the sense of distributions. Harmonic functions, which satisfy Laplace's equation, lie at the intersection of subharmonic and superharmonic functions, whereas subharmonic functions are upper semi-continuous functions dominated locally by harmonic functions, similar to how plurisubharmonic functions are upper semi-continuous and dominate holomorphic functions. The relationship highlights that convexity analogously restricts real second derivatives, while plurisubharmonicity restricts the complex Hessian, both serving as generalized convexity notions with deep connections to harmonic and subharmonic function theory.
Summary and Comparative Table
Convex functions are real-valued functions defined on convex subsets of Euclidean space, characterized by the property that their epigraphs form convex sets, ensuring local minima are global. Plurisubharmonic functions extend convexity concepts into complex analysis, defined on complex manifolds where their restriction to any complex line is subharmonic, playing a crucial role in several complex variables and complex geometry. A comparative table highlights convex functions as real-valued, globally defined on convex sets, and promoting convex optimization, while plurisubharmonic functions apply to complex domains, facilitate complex potential theory, and are instrumental in the study of complex spaces and their positivity properties.
Convex Infographic
 libterm.com
libterm.com