A dense set in mathematics is a subset of a space where every point in the space can be approximated arbitrarily closely by points from the subset. This property is essential in analysis and topology, influencing concepts like continuity and convergence. Explore the rest of the article to understand how dense sets shape various mathematical theories and applications.
Table of Comparison
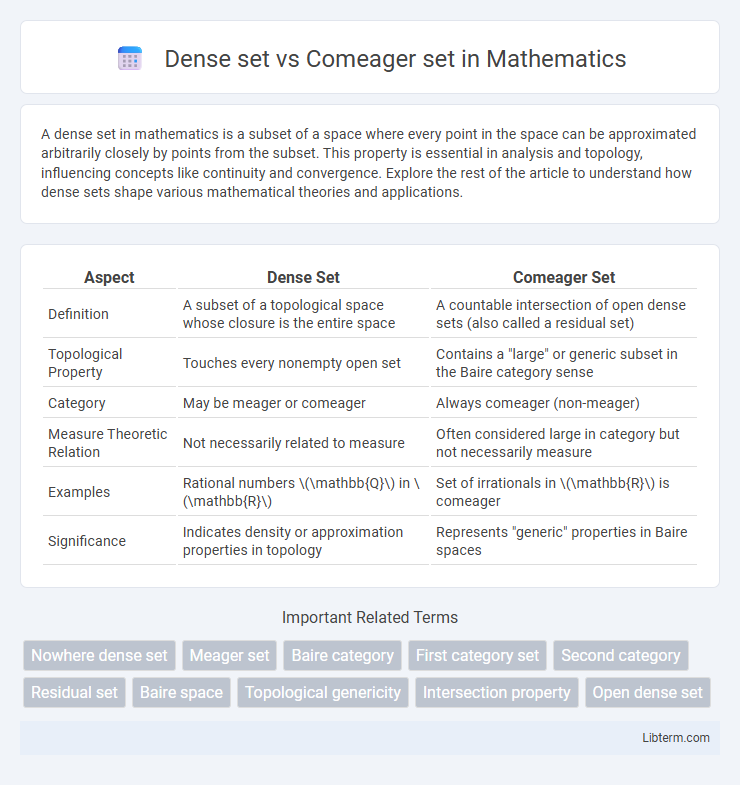
| Aspect | Dense Set | Comeager Set |
|---|---|---|
| Definition | A subset of a topological space whose closure is the entire space | A countable intersection of open dense sets (also called a residual set) |
| Topological Property | Touches every nonempty open set | Contains a "large" or generic subset in the Baire category sense |
| Category | May be meager or comeager | Always comeager (non-meager) |
| Measure Theoretic Relation | Not necessarily related to measure | Often considered large in category but not necessarily measure |
| Examples | Rational numbers \(\mathbb{Q}\) in \(\mathbb{R}\) | Set of irrationals in \(\mathbb{R}\) is comeager |
| Significance | Indicates density or approximation properties in topology | Represents "generic" properties in Baire spaces |
Introduction to Dense Sets and Comeager Sets
Dense sets in topology are subsets of a space whose closure is the entire space, meaning every point in the space either belongs to the dense set or is a limit point of it. Comeager sets, also known as residual sets, are complements of meager sets and hold a significant place in Baire category theory because they contain a countable intersection of dense open sets, making them "large" in a topological sense. Understanding the distinction between dense and comeager sets is crucial for grasping concepts such as generic properties and typical behaviors in complete metric spaces and Baire spaces.
Fundamental Definitions
A dense set in a topological space is one whose closure equals the entire space, meaning every non-empty open set intersects the dense set. A comeager set is a countable intersection of open dense sets, also known as a residual set, and it is large in the sense of Baire category. These fundamental definitions distinguish density, relating to proximity and closure, from comeagerness, emphasizing topological largeness through category theory.
Key Differences Between Dense and Comeager Sets
Dense sets in a topological space are characterized by having the property that every non-empty open set intersects them, ensuring their elements are arbitrarily close to any point in the space. Comeager sets, defined as complements of meager (first category) sets, are prevalent in Baire spaces and represent large sets in the sense of category rather than just density. Unlike dense sets, which focus on proximity and intersection with open sets, comeager sets capture a stronger notion of largeness related to countable intersections of open dense sets.
Dense Sets: Examples and Properties
Dense sets in topology are subsets of a space whose closure equals the entire space, meaning every point in the space is either in the set or arbitrarily close to it. Classic examples include the rational numbers Q within the real numbers R, illustrating density because between any two real numbers there is a rational number. Key properties highlight that dense sets have no isolated points and intersect every non-empty open set, making them crucial in approximation and continuity arguments in analysis.
Comeager Sets: Examples and Properties
Comeager sets, also known as residual sets, are subsets of a topological space whose complement is meager, meaning they contain a countable intersection of dense open sets. Examples include the set of irrational numbers in the real line, which is comeager in the usual topology, and generic points in dynamical systems often form comeager sets. Properties of comeager sets include being dense and having full Baire category, making them crucial in understanding typical behavior in complete metric spaces.
Topological Context: Baire Category Theorem
In the topological context, a dense set in a space is one whose closure equals the entire space, ensuring every open set intersects it, while a comeager set, also known as residual, is a countable intersection of open dense sets. The Baire Category Theorem states that in a complete metric space, or more generally in a Baire space, the intersection of countably many open dense sets is dense, implying comeager sets are dense and large in a topological sense. This theorem highlights the difference in "largeness" between dense sets, which may be small in measure, and comeager sets, which are topologically generic and typical.
Interplay with Nowhere Dense and Meager Sets
A dense set intersects every non-empty open subset of a topological space, while a comeager set contains a countable intersection of dense open sets, making it large in the Baire category sense. Nowhere dense sets have closures with empty interiors, and meager sets are countable unions of nowhere dense sets, representing topologically small or negligible subsets. The interplay between these concepts highlights that comeager sets are complements of meager sets, and dense sets can be dense without being comeager, emphasizing distinctions in size and genericity within topology.
Applications in Analysis and Topology
Dense sets play a crucial role in analysis and topology by ensuring that every open set in a space contains points from the dense subset, facilitating approximation and continuity arguments. Comeager sets, defined as the countable intersection of open dense sets, are fundamental in Baire category theory, often used to prove generic properties in complete metric spaces and topological groups. Applications include demonstrating typical behavior in function spaces, such as generic smoothness or differentiability, and establishing the prevalence of certain dynamical or structural phenomena in infinite-dimensional analysis.
Common Misconceptions
Dense sets are often mistakenly thought to imply a large or significant portion of a space, but they merely require every open set to contain at least one point from the dense set, regardless of measure or size. Comeager sets, defined as complements of meager (first category) sets in Baire spaces, are frequently confused with dense sets, though comeager sets represent "large" sets in a topological sense, encompassing residual properties and genericity. A key misconception is equating density with comeagerness, ignoring that dense sets can be small in measure or category, while comeager sets are always topologically large and contain dense subsets.
Summary and Further Reading
A dense set in a topological space is one whose closure equals the entire space, meaning it contains points arbitrarily close to every point in that space. A comeager set, also known as a set of second category, is a set whose complement is meager (i.e., of the first category), often characterized by being a countable intersection of dense open sets, making it "large" in a topological sense. For further reading, explore works on Baire category theorem, descriptive set theory, and topology textbooks that cover category and density concepts in detail.
Dense set Infographic
 libterm.com
libterm.com