A function is a fundamental concept in mathematics and computer science, representing a relation that assigns each input exactly one output. Understanding how functions work can improve your problem-solving skills and streamline complex calculations in various fields. Explore the rest of this article to discover different types of functions and their practical applications.
Table of Comparison
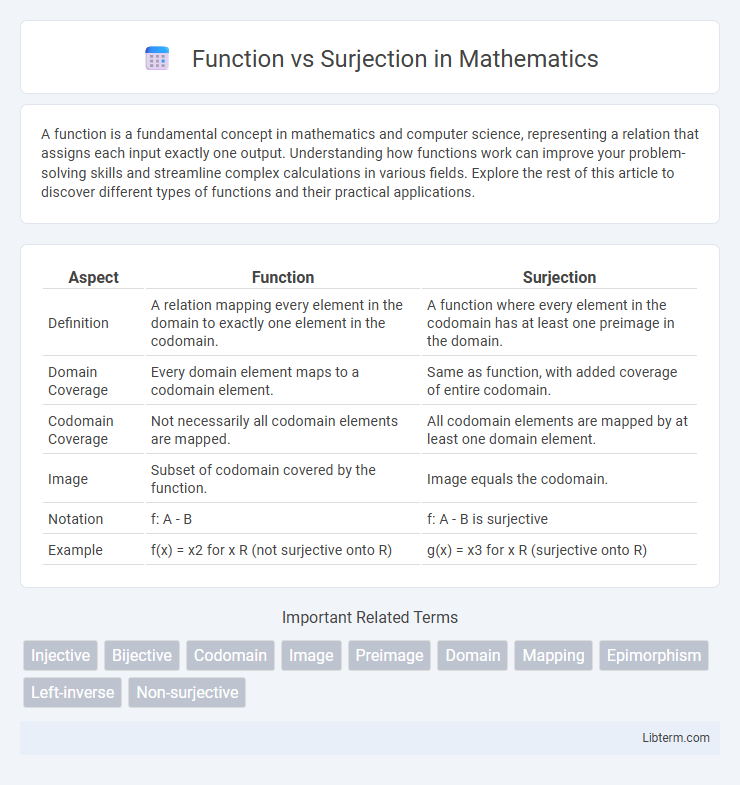
| Aspect | Function | Surjection |
|---|---|---|
| Definition | A relation mapping every element in the domain to exactly one element in the codomain. | A function where every element in the codomain has at least one preimage in the domain. |
| Domain Coverage | Every domain element maps to a codomain element. | Same as function, with added coverage of entire codomain. |
| Codomain Coverage | Not necessarily all codomain elements are mapped. | All codomain elements are mapped by at least one domain element. |
| Image | Subset of codomain covered by the function. | Image equals the codomain. |
| Notation | f: A - B | f: A - B is surjective |
| Example | f(x) = x2 for x R (not surjective onto R) | g(x) = x3 for x R (surjective onto R) |
Introduction to Functions in Mathematics
A function in mathematics is a relation that assigns each element of a domain to exactly one element in the codomain, ensuring a unique output for every input. A surjection, or onto function, is a special type of function where every element in the codomain is mapped by at least one element from the domain, covering the entire codomain. Understanding the distinction between general functions and surjective functions is fundamental in set theory, algebra, and calculus for analyzing function behavior and mapping properties.
Defining Functions: Basic Concepts
A function is a relation where each element in the domain maps to exactly one element in the codomain, ensuring a well-defined output for every input. A surjection, or onto function, is a specific type of function in which every element of the codomain has at least one preimage in the domain, meaning the function covers the entire codomain. Understanding the distinction between general functions and surjections is fundamental in set theory and mathematical analysis.
What Is a Surjection? Understanding Surjective Functions
A surjection, or onto function, is a type of mapping where every element in the codomain has at least one corresponding element in the domain. Surjective functions ensure that the function's range covers the entire codomain, meaning for every y in the codomain Y, there exists at least one x in the domain X such that f(x) = y. Understanding surjections is crucial in fields like mathematics and computer science for analyzing function behavior and establishing invertibility conditions.
Key Differences: Function vs Surjection
A function is a relation from a set of inputs to a set of possible outputs where each input is related to exactly one output, whereas a surjection (onto function) requires that every element of the codomain has at least one preimage in the domain. The key difference lies in surjections ensuring coverage of the entire codomain, unlike general functions which may leave some codomain elements unmapped. This distinction impacts mathematical proofs and mappings in fields like algebra and topology where surjective functions guarantee completeness of output sets.
Graphical Representation of Functions and Surjections
The graphical representation of a function is a set of ordered pairs where each input from the domain is mapped to exactly one output in the codomain, typically depicted as a curve or line without any vertical overlaps indicating multiple outputs for a single input. In contrast, a surjection (onto function) graph covers every element in the codomain at least once, ensuring the range equals the codomain and every y-value is achieved by some x-value. Visualizing surjections involves confirming that the graph touches every horizontal line corresponding to elements of the codomain, highlighting full coverage without gaps.
Mathematical Notation: Function and Surjection Explained
A function \( f: A \to B \) is a relation that assigns each element \( a \in A \) a unique element \( f(a) \in B \). A surjection (onto function) requires that for every \( b \in B \), there exists at least one \( a \in A \) such that \( f(a) = b \), ensuring the image of \( f \) equals the codomain \( B \). The notation for a surjective function is typically expressed as \( f: A \twoheadrightarrow B \), highlighting the onto property.
Real-World Examples of Surjective Functions
Surjective functions, also known as onto functions, map every element of the codomain to at least one element from the domain, ensuring complete coverage. Real-world examples include the assignment of workers to job roles where every role is filled, or the mapping of a set of classrooms to the students such that each classroom has at least one student. In contrast, a general function does not guarantee every element in the target set is assigned, highlighting surjection's unique role in ensuring full utilization or representation.
Importance of Surjections in Mathematical Theory
Surjections, or onto functions, play a crucial role in mathematical theory by ensuring every element of the codomain is mapped by at least one element of the domain, enabling the construction of well-defined inverse functions on their images. This property is essential in fields such as algebra and topology, where surjections facilitate quotient structures and continuous mappings onto target spaces. Understanding surjections aids in characterizing isomorphisms and bijections, which are foundational to the study of mathematical equivalences and transformations.
Comparing Injective, Surjective, and Bijective Functions
Injective functions map distinct elements in the domain to distinct elements in the codomain, ensuring no two inputs share the same output, while surjective functions cover the entire codomain, meaning every element in the codomain has at least one preimage in the domain. Bijective functions combine both properties, establishing a one-to-one correspondence between the domain and codomain, which guarantees invertibility and a perfect pairing of elements. Understanding the differences between injective, surjective, and bijective functions is fundamental in fields like set theory, linear algebra, and functional analysis.
Summary: Choosing the Right Function Type
Selecting the appropriate function type hinges on the relationship between domain and codomain elements; a function is any mapping from inputs to outputs, while a surjection ensures every element in the codomain is mapped by at least one domain element. Surjective functions are essential in contexts requiring full coverage of output values, such as solving equations where every possible output must be attainable. Understanding the distinction guides accurate modeling in mathematics, computer science, and system design, optimizing function performance and data representation.
Function Infographic
 libterm.com
libterm.com