Closed offers limited access and restricts interaction with the environment, impacting user engagement and experience. Understanding its implications can help you navigate situations where access is controlled or unavailable. Explore the rest of the article to learn how to effectively manage and adapt to closed scenarios.
Table of Comparison
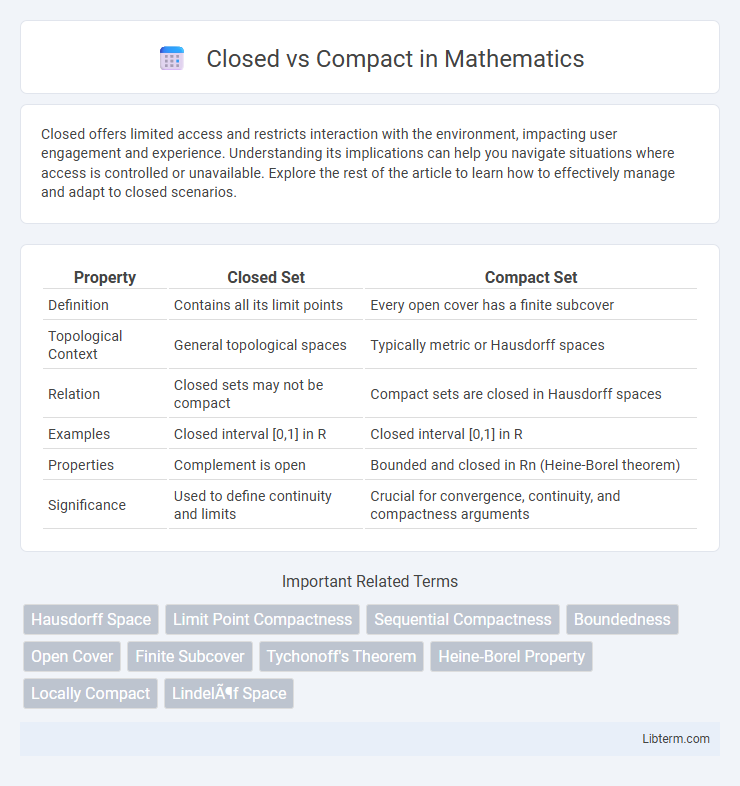
| Property | Closed Set | Compact Set |
|---|---|---|
| Definition | Contains all its limit points | Every open cover has a finite subcover |
| Topological Context | General topological spaces | Typically metric or Hausdorff spaces |
| Relation | Closed sets may not be compact | Compact sets are closed in Hausdorff spaces |
| Examples | Closed interval [0,1] in R | Closed interval [0,1] in R |
| Properties | Complement is open | Bounded and closed in Rn (Heine-Borel theorem) |
| Significance | Used to define continuity and limits | Crucial for convergence, continuity, and compactness arguments |
Understanding Closed and Compact Sets
Closed sets contain all their limit points, ensuring that any convergent sequence within the set converges to a point also inside the set, which plays a crucial role in topology and real analysis. Compact sets are characterized by being closed and bounded in metric spaces, allowing every open cover to have a finite subcover, a property essential for continuity and convergence arguments. Understanding the differences clarifies key concepts: closed sets guarantee limit point inclusion, while compact sets additionally ensure boundedness and finite subcover conditions.
Fundamental Definitions in Topology
A closed set in topology contains all its limit points, making it equal to its closure, while a compact set is one where every open cover has a finite subcover, ensuring boundedness and completeness under certain conditions. Closed sets are defined through the complement of open sets, fundamental in the structure of topological spaces, whereas compactness emphasizes the covering properties and finite subcover extraction. Understanding these definitions is crucial for analyzing continuous functions, convergence, and the overall structure of topological spaces.
Key Differences between Closed and Compact Sets
Closed sets in a topological space contain all their limit points, ensuring the inclusion of boundary elements and making them complete with respect to convergence. Compact sets are those where every open cover has a finite subcover, guaranteeing properties like boundedness and sequential compactness in metric spaces. Key differences lie in their definitions and implications: closed sets emphasize boundary adherence, while compact sets focus on covering properties and finiteness conditions.
Examples of Closed Sets
Examples of closed sets include the interval [0, 1] in the real numbers, which contains all its limit points, and any finite set, such as {2, 4, 6}, which trivially meets the closed set criteria. In Euclidean space, closed balls like {x R^n : ||x - a|| <= r} represent another classic example, encompassing points at a fixed distance or less from center a. Conversely, sets like (0, 1) lack closure because they exclude boundary points, highlighting the fundamental difference between closed and compact sets.
Examples of Compact Sets
Compact sets include closed intervals like [0, 1] in the real numbers, which contain all their limit points and are bounded. Another example is a closed disk in the Euclidean plane, defined as all points within a fixed radius from a center, including the boundary. Finite sets of points are also compact, as they are both closed and bounded in any metric space.
Closed vs Compact in Metric Spaces
Closed sets in metric spaces contain all their limit points, ensuring any convergent sequence within the set converges to a point also in the set. Compact sets are closed and bounded, with every open cover admitting a finite subcover, implying sequential compactness where every sequence has a convergent subsequence in the set. The distinction lies in closed sets possibly being unbounded or non-compact, while compactness guarantees both closure and boundedness, key properties in analysis and topology.
Importance in Real Analysis
Closed sets play a crucial role in real analysis due to their property of containing all their limit points, which ensures the convergence of sequences within the set. Compact sets, characterized by being closed and bounded in Euclidean spaces, guarantee the existence of maximum and minimum values for continuous functions, making them essential for optimization problems. The interplay between closed and compact sets underpins key results such as the Heine-Borel theorem, which is fundamental for understanding continuity, convergence, and function behavior in real analysis.
Applications in Mathematics and Science
Closed and compact sets are fundamental concepts in topology with distinct applications in mathematics and science. Closed sets, which contain all their limit points, are crucial in defining convergence and continuity, enabling precise solutions in analysis and differential equations. Compact sets, characterized by every open cover having a finite subcover, ensure properties like boundedness and completeness, playing a key role in optimization problems, stability analysis, and the convergence of sequences in functional spaces.
Common Misconceptions Explained
Closed and compact sets are often confused, but they differ significantly in topology; a closed set contains all its limit points while a compact set is one where every open cover has a finite subcover. A common misconception is assuming all closed sets are compact, which holds true only in finite-dimensional Euclidean spaces. In infinite-dimensional or more general topological spaces, compactness implies closedness but not vice versa, highlighting the importance of understanding the underlying space's structure.
Summary: Choosing the Right Concept
Closed and compact spaces differ fundamentally in topology; closed sets contain all their limit points, making them complete in terms of boundary, while compact sets are both closed and bounded, ensuring every open cover has a finite subcover. Choosing between closed and compact concepts depends on the desired properties for continuity, convergence, and optimization in mathematical analysis or applied contexts. Compactness often facilitates stronger results in function analysis and convergence, whereas closedness is essential for boundary completeness and limit inclusion.
Closed Infographic
 libterm.com
libterm.com