The operator norm measures the "size" or "strength" of a bounded linear operator between normed vector spaces, capturing how much it can stretch a vector. It is defined as the supremum of the norms of the image vectors over all unit vectors, providing a crucial tool in functional analysis and related fields. Explore the rest of the article to understand how the operator norm is computed and applied in various mathematical contexts.
Table of Comparison
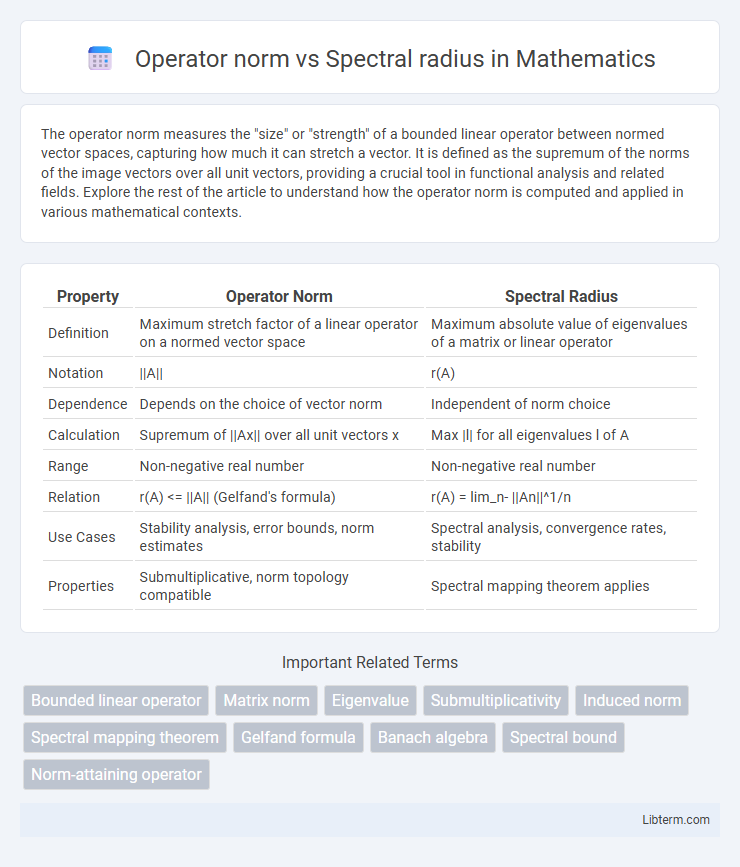
| Property | Operator Norm | Spectral Radius |
|---|---|---|
| Definition | Maximum stretch factor of a linear operator on a normed vector space | Maximum absolute value of eigenvalues of a matrix or linear operator |
| Notation | ||A|| | r(A) |
| Dependence | Depends on the choice of vector norm | Independent of norm choice |
| Calculation | Supremum of ||Ax|| over all unit vectors x | Max |l| for all eigenvalues l of A |
| Range | Non-negative real number | Non-negative real number |
| Relation | r(A) <= ||A|| (Gelfand's formula) | r(A) = lim_n- ||An||^1/n |
| Use Cases | Stability analysis, error bounds, norm estimates | Spectral analysis, convergence rates, stability |
| Properties | Submultiplicative, norm topology compatible | Spectral mapping theorem applies |
Introduction to Operator Norm and Spectral Radius
Operator norm measures the maximum stretching effect of a linear operator on vectors in a normed space, quantifying the largest possible amplification of vector magnitude. Spectral radius is defined as the largest absolute value of the eigenvalues of a linear operator and reflects the asymptotic growth rate of the operator's powers. These two concepts are fundamental in functional analysis, with the operator norm providing a norm-based bound and the spectral radius connecting to the operator's long-term behavior.
Fundamental Definitions
The operator norm of a matrix measures the maximum stretching factor the matrix applies to any unit vector, defined as the supremum of the norm of Ax over all unit vectors x. The spectral radius is the largest absolute value of the eigenvalues of the matrix, capturing its asymptotic behavior under iteration. Understanding the operator norm provides bounds on matrix behavior, while the spectral radius characterizes long-term stability and convergence properties.
Historical Context and Mathematical Significance
The operator norm and spectral radius have distinct origins in linear algebra and functional analysis, with the operator norm emerging from the need to measure the size of linear transformations in normed vector spaces. The spectral radius, defined as the largest absolute value of an operator's eigenvalues, gained prominence through its role in characterizing stability and convergence properties of linear operators. Their mathematical significance lies in the operator norm providing bounds on operator behavior, while the spectral radius offers critical insight into long-term dynamics and spectral properties of matrices and operators.
Calculation Methods for Operator Norm
The operator norm is typically calculated using the supremum of the norm of the matrix acting on unit vectors, often expressed as \(\|A\| = \sup_{\|x\|=1} \|Ax\|\). In the case of matrices, this involves computing the largest singular value, which can be found via singular value decomposition (SVD) or by evaluating the square root of the largest eigenvalue of \(A^*A\). Unlike the spectral radius, which is the maximum absolute value of eigenvalues, the operator norm measures the maximal stretching factor of the operator in vector space.
Approaches for Determining Spectral Radius
The spectral radius of a matrix is determined by identifying the largest absolute value among its eigenvalues, often computed through algorithms such as the power iteration method or Gershgorin circle theorem for bounds. Operator norm, however, measures the maximum stretching factor a matrix induces on vectors, with common norms including the induced 2-norm related to the largest singular value. Approaches for estimating spectral radius prioritize eigenvalue-specific techniques, whereas operator norm calculations rely on matrix-induced norms, highlighting their distinct computational strategies.
Key Differences between Operator Norm and Spectral Radius
The operator norm measures the maximum stretching effect of a linear operator on a vector, while the spectral radius is the largest absolute value of the operator's eigenvalues. The operator norm is always greater than or equal to the spectral radius, reflecting the widest possible expansion across all vectors. Spectral radius informs about asymptotic behavior and stability, whereas the operator norm provides bounds on the operator's magnitude in a given normed space.
Theoretical Relationships and Inequalities
The operator norm and spectral radius of a linear operator are linked by Gelfand's formula, which states that the spectral radius equals the limit of the nth root of the operator norm raised to the nth power as n approaches infinity. The spectral radius is always bounded above by the operator norm, establishing the inequality r(A) <= ||A|| for any bounded linear operator A on a Banach space. In finite-dimensional spaces, the spectral radius provides a lower bound on the asymptotic behavior of the operator norm sequence, reflecting fundamental theoretical relationships in functional analysis.
Applications in Functional Analysis and Linear Algebra
The operator norm quantifies the maximum stretching factor of a linear operator on a vector space, crucial in stability analysis and convergence of iterative methods in functional analysis. The spectral radius, defined as the largest absolute value of eigenvalues, determines the long-term behavior of powers of an operator, playing a key role in spectral theory and matrix diagonalization. Applications include bounding spectral radius by operator norm to assess operator invertibility and estimating growth rates in dynamical systems and Markov chains within linear algebra.
Practical Examples and Case Studies
The operator norm measures the largest stretching factor of a linear operator on a vector space, commonly used to assess matrix stability in numerical analysis and signal processing. Spectral radius, defined as the largest absolute eigenvalue, plays a crucial role in predicting long-term behavior in iterative methods like power iteration and Markov chains. Practical case studies reveal that while operator norm bounds error magnitudes, spectral radius determines convergence rates and stability in systems such as Google's PageRank algorithm and dynamic network models.
Conclusion and Further Reading
The operator norm provides an upper bound for the spectral radius, indicating that the magnitude of the largest eigenvalue cannot exceed the chosen norm of the operator. This relationship is crucial in stability analysis and iterative methods for solving linear systems. For deeper insights, consult texts on functional analysis, matrix theory, and spectral theory such as "Matrix Analysis" by Horn and Johnson or "Functional Analysis" by Rudin.
Operator norm Infographic
 libterm.com
libterm.com