The Mellin transform is a powerful integral transform used to analyze functions by converting them into a complex frequency domain, facilitating problems in number theory, probability, and asymptotic analysis. Its unique scaling properties make it particularly useful for solving differential equations and evaluating complex integrals involving products and ratios of variables. Discover how the Mellin transform can enhance your mathematical toolbox by exploring its applications and techniques in the full article.
Table of Comparison
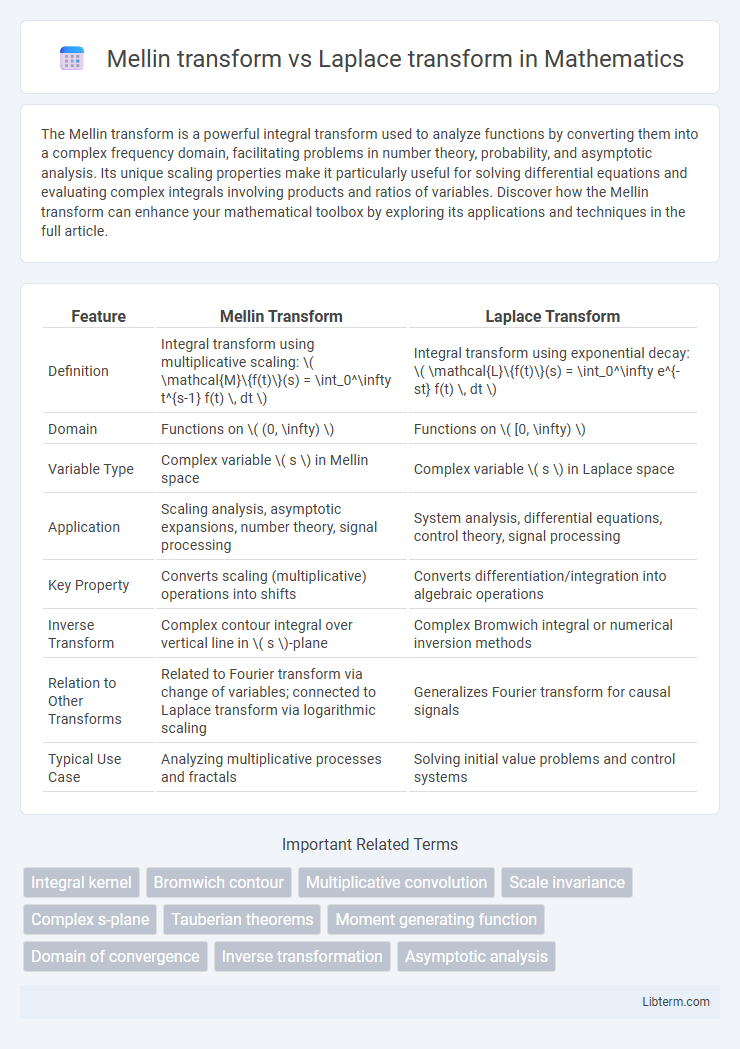
| Feature | Mellin Transform | Laplace Transform |
|---|---|---|
| Definition | Integral transform using multiplicative scaling: \( \mathcal{M}\{f(t)\}(s) = \int_0^\infty t^{s-1} f(t) \, dt \) | Integral transform using exponential decay: \( \mathcal{L}\{f(t)\}(s) = \int_0^\infty e^{-st} f(t) \, dt \) |
| Domain | Functions on \( (0, \infty) \) | Functions on \( [0, \infty) \) |
| Variable Type | Complex variable \( s \) in Mellin space | Complex variable \( s \) in Laplace space |
| Application | Scaling analysis, asymptotic expansions, number theory, signal processing | System analysis, differential equations, control theory, signal processing |
| Key Property | Converts scaling (multiplicative) operations into shifts | Converts differentiation/integration into algebraic operations |
| Inverse Transform | Complex contour integral over vertical line in \( s \)-plane | Complex Bromwich integral or numerical inversion methods |
| Relation to Other Transforms | Related to Fourier transform via change of variables; connected to Laplace transform via logarithmic scaling | Generalizes Fourier transform for causal signals |
| Typical Use Case | Analyzing multiplicative processes and fractals | Solving initial value problems and control systems |
Introduction to Integral Transforms
The Mellin transform converts functions into complex frequency domains by integrating against power functions, which is particularly effective for analyzing scaling properties. The Laplace transform, on the other hand, integrates functions against exponential decays, facilitating the study of time-domain systems and differential equations. Both integral transforms serve as fundamental tools in signal processing and applied mathematics, enabling problem-solving through domain conversion.
Overview of Laplace Transform
The Laplace transform is an integral transform widely used in engineering and physics to convert time-domain functions into complex frequency-domain representations, facilitating the analysis of linear time-invariant systems. It transforms a function f(t) defined for t >= 0 into F(s) by integrating e^(-st)f(t) from 0 to infinity, where s is a complex number. This transform simplifies differential equations into algebraic equations, enabling easier manipulation, solution, and system characterization compared to time-domain analysis.
Overview of Mellin Transform
The Mellin transform is a powerful integral transform used primarily in complex analysis and number theory, converting functions into a multiplicative scale by integrating over positive real numbers with a kernel involving powers of the variable. Unlike the Laplace transform, which maps functions from the time domain to the complex frequency domain to analyze linear time-invariant systems, the Mellin transform excels in solving problems with scale invariance and multiplicative convolution. Its applications include asymptotic analysis, image processing, and the study of fractals, leveraging its ability to handle products and scaling properties efficiently.
Mathematical Formulations
The Mellin transform is defined as M{f}(s) = 0^ x^(s-1) f(x) dx, emphasizing multiplicative scaling properties through the complex variable s. In contrast, the Laplace transform L{f}(s) = 0^ e^(-st) f(t) dt involves an exponential kernel e^(-st) and is widely used for analyzing systems described by linear differential equations. Both transforms convert functions into complex frequency domains but differ fundamentally in their kernels, where Mellin addresses power-law behaviors and Laplace handles exponential decays.
Domains of Application
The Mellin transform is widely used in number theory, fractal analysis, and solving problems involving scale invariance, such as image processing and asymptotic expansions. The Laplace transform is primarily applied in engineering fields for solving differential equations, control systems, and signal processing due to its ability to handle initial value problems in the time domain. Both transforms convert complex functions into more manageable forms but serve different purposes based on their unique properties and application domains.
Key Theoretical Differences
The Mellin transform converts functions by integrating over positive real numbers weighted by a power function, emphasizing scale invariance and multiplicative structures, while the Laplace transform integrates functions over the positive real axis with an exponential decay kernel, focusing on time-domain analysis and stability. The Mellin transform's kernel is \( x^{s-1} \), making it ideal for analyzing asymptotic behaviors and products, whereas the Laplace transform's kernel is \( e^{-st} \), suited for differential equations and causal systems. These fundamental differences result in distinct regions of convergence and inversion formulas tailored to their respective domains and applications.
Use Cases in Engineering and Science
The Mellin transform is extensively used in image processing, signal analysis, and fractal geometry for scaling and pattern recognition, especially when dealing with multiplicative processes and scale-invariant systems. The Laplace transform excels in solving differential equations, control systems, and electrical engineering problems by converting time-domain functions into the complex frequency domain to analyze stability and dynamics. Engineers and scientists select the Mellin transform for applications involving scale changes and asymptotic analysis, while the Laplace transform is preferred for linear time-invariant system analysis and transient response evaluation.
Laplace vs Mellin: Comparative Advantages
The Laplace transform excels in solving linear time-invariant differential equations and system analysis, especially for initial value problems and real-time signal processing. The Mellin transform offers superior capabilities in scale-invariant problems, asymptotic analysis, and multiplicative convolution, making it ideal for image processing and number theory applications. Choosing between Laplace and Mellin transforms depends on the problem domain: temporal analysis favors Laplace, while scale or multiplicative structure benefits from Mellin.
Conversion and Relationships Between Transforms
The Mellin transform converts a function f(t) into an integral over t^s-1 f(t), relating closely to scale-invariant problems, while the Laplace transform integrates f(t) against e^{-st}, emphasizing exponential decay. The Mellin transform can be viewed as a Laplace transform in logarithmic variables, linking Mellin variable s to Laplace variable through s = c + io, where the Mellin transform is essentially the Laplace transform of f(e^x) weighted by e^{cx}. This intrinsic relationship allows conversion techniques between the two transforms, enabling applications across signal processing, complex analysis, and asymptotic evaluation.
Choosing the Right Transform for Your Problem
The Mellin transform excels in analyzing scale-invariant problems and multiplicative processes, making it ideal for applications in image processing and fractal analysis. The Laplace transform is better suited for solving linear differential equations and control systems with time-dependent behavior due to its handling of exponential decay and growth. Selecting between the two transforms depends on whether the problem involves scaling properties or temporal dynamics, guiding the choice for an efficient and accurate mathematical solution.
Mellin transform Infographic
 libterm.com
libterm.com