A Dedekind domain is a type of integral domain characterized by its property that every nonzero proper ideal factors uniquely into prime ideals. These domains play a crucial role in algebraic number theory and commutative algebra due to their ideal-theoretic behavior resembling that of the ring of integers. Discover more about the structure and applications of Dedekind domains in the rest of the article.
Table of Comparison
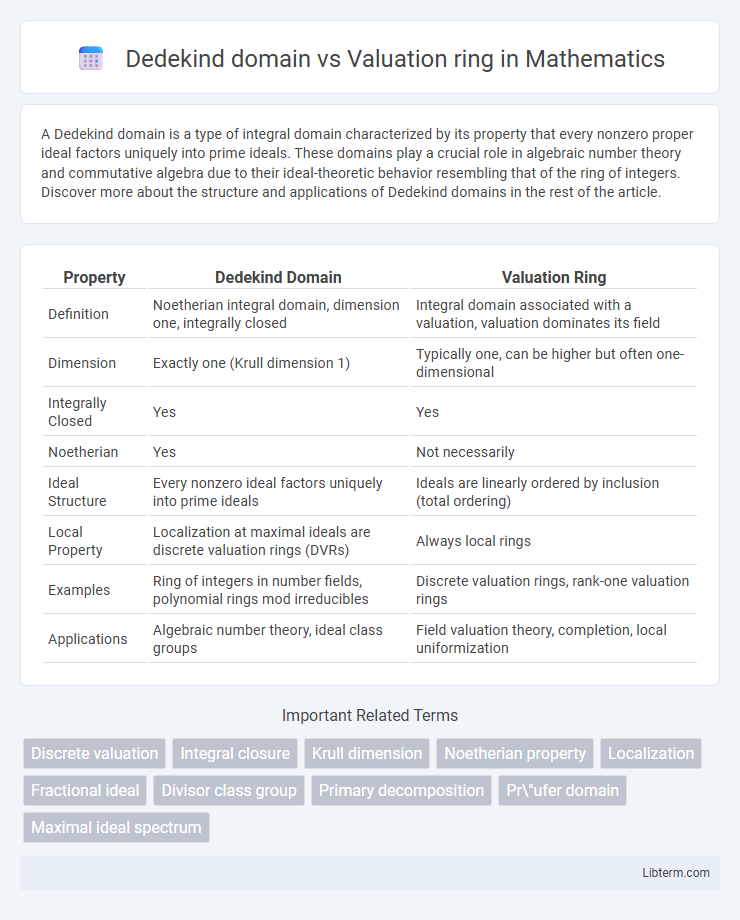
| Property | Dedekind Domain | Valuation Ring |
|---|---|---|
| Definition | Noetherian integral domain, dimension one, integrally closed | Integral domain associated with a valuation, valuation dominates its field |
| Dimension | Exactly one (Krull dimension 1) | Typically one, can be higher but often one-dimensional |
| Integrally Closed | Yes | Yes |
| Noetherian | Yes | Not necessarily |
| Ideal Structure | Every nonzero ideal factors uniquely into prime ideals | Ideals are linearly ordered by inclusion (total ordering) |
| Local Property | Localization at maximal ideals are discrete valuation rings (DVRs) | Always local rings |
| Examples | Ring of integers in number fields, polynomial rings mod irreducibles | Discrete valuation rings, rank-one valuation rings |
| Applications | Algebraic number theory, ideal class groups | Field valuation theory, completion, local uniformization |
Introduction to Dedekind Domains and Valuation Rings
Dedekind domains are integral domains in which every nonzero ideal factors uniquely into prime ideals, providing a foundational structure in algebraic number theory and algebraic geometry. Valuation rings generalize the concept of discrete valuation rings by associating elements to values in a totally ordered abelian group, characterizing local rings with a valuation that measures divisibility. The interplay between Dedekind domains and valuation rings arises as Dedekind domains can be described locally by valuation rings, linking ideal factorization to valuation theory.
Defining Dedekind Domains
Dedekind domains are integral domains in which every nonzero proper ideal factors uniquely into prime ideals, characterized by being Noetherian, integrally closed, and having Krull dimension one. Valuation rings are local integral domains where for every element in the field of fractions, either the element or its inverse lies in the ring, providing a total ordering on ideals via divisibility. While valuation rings represent local descriptions associated with valuations, Dedekind domains generalize the ideal factorization property globally across all nonzero ideals.
Understanding Valuation Rings
Valuation rings are integral domains where for every element in its field of fractions, either the element or its inverse is in the ring, enabling a total order of divisibility reflecting valuation theory. Unlike Dedekind domains, which are Noetherian, integrally closed, and have dimension one with well-behaved ideal factorization, valuation rings may not be Noetherian and can have higher Krull dimensions, emphasizing valuation-induced local properties. Understanding valuation rings involves analyzing their local and valuation-theoretic structures, which provide a foundation for studying completions and extensions in fields with valuation.
Key Properties of Dedekind Domains
Dedekind domains are Noetherian integral domains characterized by the unique factorization of every nonzero proper ideal into a product of prime ideals, a property not generally held by valuation rings. Unlike valuation rings, which are local and capture valuation behavior through a total ordering of ideals, Dedekind domains exhibit a global structure with finitely many maximal ideals but maintain a well-defined ideal class group reflecting their arithmetic complexity. Their key properties include integrally closedness, dimension one, and the condition that every nonzero prime ideal is maximal, making Dedekind domains fundamental in algebraic number theory and algebraic geometry.
Essential Characteristics of Valuation Rings
Valuation rings are integral domains where for every element in the field of fractions, either the element or its inverse lies in the ring, making them local and integrally closed with a total ordering on their ideals. Unlike Dedekind domains, which are Noetherian, integrally closed, and have dimension one, valuation rings may be non-Noetherian but retain a well-structured valuation function reflecting divisibility. The essential characteristic of valuation rings lies in their ability to measure sizes or multiplicities via valuations, providing a unique local perspective on the arithmetic geometry of fields.
Differences in Ideal Structure
Dedekind domains have every nonzero ideal factor uniquely into prime ideals, reflecting a well-structured class group and ideal factorization property. In contrast, valuation rings possess a totally ordered ideal set, where every ideal is comparable, resulting in a valuation that measures divisibility directly. This fundamental difference in ideal structure distinguishes Dedekind domains' unique factorization of ideals from valuation rings' linear ordering of ideals based on valuations.
Comparative Examples in Algebraic Number Theory
A Dedekind domain is an integral domain where every nonzero ideal factors uniquely into prime ideals, commonly exemplified by the ring of integers in a number field, whereas a valuation ring is a local integral domain that corresponds to a valuation on a field, such as the ring of p-adic integers within the field of p-adic numbers. In algebraic number theory, Dedekind domains provide a global perspective on factorization of ideals, while valuation rings offer a local viewpoint by emphasizing valuation and completions at primes. For instance, the localization of a Dedekind domain at a prime ideal yields a valuation ring, illustrating how valuation rings serve as local building blocks in the structure theory of algebraic integers.
Applications in Algebraic Geometry
Dedekind domains serve as foundational structures in algebraic geometry for studying one-dimensional schemes, particularly in the classification of algebraic curves and their divisor class groups. Valuation rings provide a local perspective, enabling the analysis of valuations and completions essential for resolving singularities and understanding local properties of algebraic varieties. Both concepts are crucial in examining the fine structure of algebraic varieties and facilitating applications such as resolution of singularities and arithmetic geometry.
Advantages and Limitations of Each Structure
Dedekind domains provide a robust framework for factorization of ideals into prime ideals, ensuring unique factorization in the ideal sense, which is invaluable in algebraic number theory and algebraic geometry; however, they require Noetherian, integrally closed, and dimension-one conditions, limiting their applicability in more general ring settings. Valuation rings offer a more flexible approach by encoding valuation data through a totally ordered value group, facilitating local analysis and branch behavior in fields, but their lack of Noetherian property and possible infinite Krull dimension make them less suitable for global structural results. Choosing between Dedekind domains and valuation rings depends on the need for ideal factorization properties versus valuation-theoretic information in algebraic and arithmetic contexts.
Summary: Choosing Between Dedekind Domains and Valuation Rings
Dedekind domains offer a well-structured framework for studying algebraic number fields with unique factorization of ideals, making them ideal for global algebraic applications. Valuation rings provide a local perspective, emphasizing valuation theory and ideal structure that is essential in local field analysis and valuation extensions. Selecting between these depends on whether the focus is on global factorization properties in number theory (Dedekind domains) or local valuation properties and completions (valuation rings).
Dedekind domain Infographic
 libterm.com
libterm.com