A simplicial complex is a mathematical structure made up of points, line segments, triangles, and higher-dimensional analogs that are combined in a well-defined manner to form a topological space. It plays a crucial role in algebraic topology, allowing the study of shapes and spaces using combinatorial methods. Explore the rest of the article to understand how simplicial complexes contribute to various fields like data analysis and geometry.
Table of Comparison
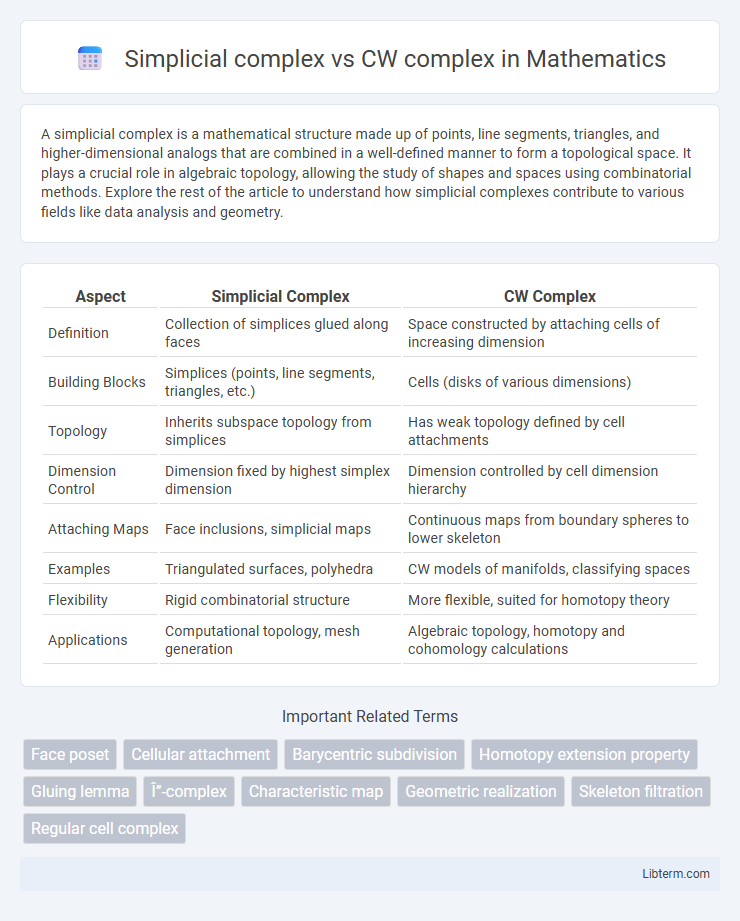
| Aspect | Simplicial Complex | CW Complex |
|---|---|---|
| Definition | Collection of simplices glued along faces | Space constructed by attaching cells of increasing dimension |
| Building Blocks | Simplices (points, line segments, triangles, etc.) | Cells (disks of various dimensions) |
| Topology | Inherits subspace topology from simplices | Has weak topology defined by cell attachments |
| Dimension Control | Dimension fixed by highest simplex dimension | Dimension controlled by cell dimension hierarchy |
| Attaching Maps | Face inclusions, simplicial maps | Continuous maps from boundary spheres to lower skeleton |
| Examples | Triangulated surfaces, polyhedra | CW models of manifolds, classifying spaces |
| Flexibility | Rigid combinatorial structure | More flexible, suited for homotopy theory |
| Applications | Computational topology, mesh generation | Algebraic topology, homotopy and cohomology calculations |
Introduction to Simplicial and CW Complexes
Simplicial complexes are built from simplices such as points, line segments, triangles, and their higher-dimensional analogs, assembled via face maps to form a combinatorial structure suitable for algebraic topology. CW complexes generalize this by attaching cells of varying dimensions inductively, using continuous maps called attaching maps that allow more flexible topological constructions beyond simplicial decompositions. Both frameworks provide foundational tools in topology for studying spaces through decomposition, but CW complexes often offer greater adaptability in handling homotopy and cell attachment complexity.
Definitions: Simplicial Complex Explained
A simplicial complex is a combinatorial structure composed of vertices, edges, triangles, and their higher-dimensional counterparts called simplices, assembled in a way that any face of a simplex is also part of the complex. It provides a rigid geometric framework ideal for computational topology and algebraic topology applications, where simplices are glued along their faces in a discrete manner. In contrast, a CW complex allows cells attached in a more flexible way using continuous maps, generalizing simplicial complexes and enabling more complex topological constructions.
Definitions: CW Complex Overview
A CW complex is a topological space constructed by gluing cells of varying dimensions, called n-cells, together in a structured way using characteristic maps from closed n-dimensional disks to the space. This construction starts with a discrete set of 0-cells (points), and higher-dimensional cells are attached inductively, ensuring closure-finite and weak topology conditions are satisfied. The CW complex framework provides a flexible and general approach to building and studying spaces in algebraic topology, differing from simplicial complexes by allowing cells that are not necessarily simplices and supporting more complex attaching maps.
Construction Methods: Simplicial vs CW Complexes
Simplicial complexes are constructed by gluing simplices (points, line segments, triangles, and their higher-dimensional analogs) along their faces using affine maps, ensuring each intersection is a simplex itself. CW complexes are built by inductively attaching cells of increasing dimensions via continuous maps from the boundary of an n-dimensional disk to the existing complex, allowing more general attaching maps and flexible subdivision. This fundamental difference in construction methods means simplicial complexes are combinatorially rigid, while CW complexes allow for more topological versatility and easier handling of spaces with complicated local structures.
Topological Properties Comparison
Simplicial complexes consist of simplices glued together along faces, providing a combinatorial framework ideal for computational topology and homology computations. CW complexes generalize this structure by attaching cells of varying dimensions via continuous maps, allowing for more flexible topological modeling and often simplifying homotopy and homology analysis. While both preserve homotopy equivalence, CW complexes facilitate easier construction and decomposition of spaces with complicated topology, whereas simplicial complexes enable explicit combinatorial descriptions beneficial for algorithmic applications.
Homotopy and Homology in Both Complexes
Simplicial complexes and CW complexes both serve as foundational structures in algebraic topology for studying homotopy and homology, with simplicial complexes offering combinatorial simplicity through well-defined simplices that facilitate explicit computation of simplicial homology and homotopy groups. CW complexes provide greater flexibility, allowing the attachment of cells of varying dimensions, which supports advanced homotopy analysis via cellular homology and enables efficient computation of homology groups using cellular chain complexes. Both complexes preserve homotopy invariance, but CW complexes accommodate more general spaces and often simplify homotopy extension and lifting problems compared to the strictly combinatorial framework of simplicial complexes.
Examples: Simplicial Complexes in Practice
Simplicial complexes are extensively used in topological data analysis, where finite sets of vertices, edges, and higher-dimensional simplices model multidimensional data structures such as social networks or biological systems. A practical example includes the Vietoris-Rips complex, which constructs simplicial complexes from point cloud data to study shape properties and connectivity at various scales. These examples highlight the computational advantage and intuitive geometric nature of simplicial complexes compared to the more flexible but abstract CW complexes.
Examples: CW Complexes in Practice
CW complexes, such as the torus constructed by gluing squares along edges, offer flexible and intuitive models for complex topological spaces compared to simplicial complexes, which rely strictly on simplices like triangles and tetrahedra. Examples in practice include the use of CW complexes for representing surfaces with holes or handles, often encountered in algebraic topology and manifold theory. This adaptability makes CW complexes especially valuable for homotopy classification and cellular homology computations where simplicial structures may be too rigid or cumbersome.
Advantages and Limitations of Each Structure
Simplicial complexes offer straightforward combinatorial structures ideal for computational topology and homology calculations, but they often require a large number of simplices to approximate spaces, leading to complex computations. CW complexes provide greater flexibility with cells of varying dimensions and more general attaching maps, enabling efficient representation of complicated topological spaces, though their combinatorial complexity can hinder algorithmic applications. Simplicial complexes excel in explicit geometric interpretation while CW complexes are advantageous for theoretical topology due to their ability to model spaces with fewer, more abstract building blocks.
Applications and Use Cases in Topology
Simplicial complexes are widely used in computational topology and data analysis, particularly for persistent homology and mesh generation due to their combinatorial structure and ease of algorithmic implementation. CW complexes provide a more flexible and general framework for modeling topological spaces in algebraic topology, enabling applications in homotopy theory, the study of manifolds, and spectral sequences. Both structures support the classification of topological spaces, but simplicial complexes excel in discrete computations while CW complexes allow more efficient handling of complicated cell attachments in higher-dimensional topology.
Simplicial complex Infographic
 libterm.com
libterm.com